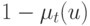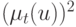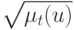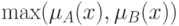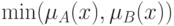|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Лингвистическая нечеткая логика
Понятие лингвистической переменной
Лингвистическая переменная отличается от числовой переменной тем, что ее значениями являются не числа, а слова или предложения в естественном или формальном языке. Поскольку слова в общем менее точны, чем числа, понятие лингвистической переменной дает возможность приближенно описывать явления, которые настолько сложны, что не поддаются описанию в общепринятых количественных терминах. В частности, нечеткое множество, которое представляет собой ограничение, связанное со значениями лингвистической переменной, можно рассматривать как совокупную характеристику различных подклассов элементов универсального множества. В этом смысле роль нечетких множеств аналогична той роли, которую играют слова и предложения в естественном языке. Например, прилагательное "КРАСИВЫЙ" отражает комплекс характеристик внешности индивидуума. Это прилагательное можно также рассматривать как название нечеткого множества, которое является ограничением, обусловленным нечеткой переменной "КРАСИВЫЙ". С этой точки зрения термины "ОЧЕНЬ КРАСИВЫЙ", "НЕКРАСИВЫЙ", "ЧЕРЕЗВЫЧАЙНО КРАСИВЫЙ", "ВПОЛНЕ КРАСИВЫЙ" и т.п. — названия нечетких множеств, образованных путем действия модификаторов "ОЧЕНЬ, НЕ, ЧЕРЕЗВЫЧАЙНО, ВПОЛНЕ" и т.п. на нечеткое множество "КРАСИВЫЙ". В сущности, эти нечеткие множества вместе с нечетким множеством "КРАСИВЫЙ" играют роль значений лингвистической переменной "ВНЕШНОСТЬ".
Важный аспект понятия лингвистической переменной состоит в том, что эта
переменная
более высокого порядка, чем нечеткая переменная, в том смысле, что значениями
лингвистической переменной являются нечеткие переменные. Например, значениями
лингвистической переменной "ВОЗРАСТ" могут быть: "МОЛОДОЙ,
НЕМОЛОДОЙ, СТАРЫЙ,
ОЧЕНЬ СТАРЫЙ, НЕ МОЛОДОЙ И НЕ СТАРЫЙ" и т.п. Каждое из этих значений
является
названием нечеткой переменной. Если  — название нечеткой
переменной,
то ограничение, обусловленное этим названием, можно интерпретировать
как смысл нечеткой переменной
— название нечеткой
переменной,
то ограничение, обусловленное этим названием, можно интерпретировать
как смысл нечеткой переменной  .
.
Другой важный аспект понятия лингвистической переменной состоит в том, что лингвистической переменной присущи два правила:
- Cинтаксическое, которое может быть задано в форме грамматики, порождающей название значений переменной;
- Cемантическое, которое определяет алгоритмическую процедуру для вычисления смысла каждого значения.
Определение. Лингвистическая переменная характеризуется набором свойств 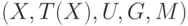 , в котором:
, в котором:
 — название переменной;
— название переменной;
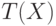 обозначает терм-множество переменной
обозначает терм-множество переменной  , т.е.
множество
названий лингвистических значений переменной
, т.е.
множество
названий лингвистических значений переменной  , причем каждое из
таких значений
является нечеткой переменной
, причем каждое из
таких значений
является нечеткой переменной  со значениями из универсального
множества
со значениями из универсального
множества  с базовой переменной
с базовой переменной  ;
;
 — синтаксическое правило, порождающее
названия
— синтаксическое правило, порождающее
названия  значений переменной
значений переменной  ;
;
 — семантическое правило, которое ставит в соответствие каждой
нечеткой переменной
— семантическое правило, которое ставит в соответствие каждой
нечеткой переменной  ее смысл
ее смысл 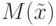 , т.е.
нечеткое подмножество
, т.е.
нечеткое подмножество 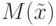 универсального множества
универсального множества  .
.
Конкретное название  , порожденное синтаксическим правилом
, порожденное синтаксическим правилом  ,
называется термом. Терм, который состоит из одного слова или из нескольких
слов, всегда фигурирующих вместе друг с другом, называется атомарным термом.
Терм, который состоит из более чем одного атомарного терма, называется
составным термом.
,
называется термом. Терм, который состоит из одного слова или из нескольких
слов, всегда фигурирующих вместе друг с другом, называется атомарным термом.
Терм, который состоит из более чем одного атомарного терма, называется
составным термом.
Пример.
Рассмотрим лингвистическую переменную с именем 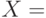 "ТЕМПЕРАТУРА В
КОМНАТЕ".
Тогда оставшуюся четверку
"ТЕМПЕРАТУРА В
КОМНАТЕ".
Тогда оставшуюся четверку 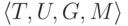 , можно определить так:
, можно определить так:
- универсальное множество U=[5,35];
-
терм-множество T={"ХОЛОДНО",
"КОМФОРТНО", "ЖАРКО"} с такими
функциями принадлежностями:
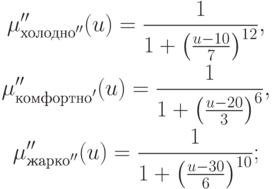
- синтаксическое правило
 , порождающее новые термы с
использованием
квантификаторов "и", "или", "не",
"очень", "более-менее" и других;
, порождающее новые термы с
использованием
квантификаторов "и", "или", "не",
"очень", "более-менее" и других; -
 будет являться процедурой, ставящей каждому новому терму
в соответствие
нечеткое множество из
будет являться процедурой, ставящей каждому новому терму
в соответствие
нечеткое множество из  по правилам: если термы
по правилам: если термы  и
и  имели функции
принадлежности
имели функции
принадлежности  и
и  соответственно, то новые термы будут
иметь следующие функции принадлежности, заданные в таблице:
соответственно, то новые термы будут
иметь следующие функции принадлежности, заданные в таблице:

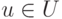 )
)