|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Методы построения функции принадлежности. Обзор основных методов
Методы построения терм-множеств
Считается, что для практических задач достаточно наличия нечеткого языка с
фиксированным
конечным словарем — ограничение не слишком сильное с точки зрения
практического использования. Лингвистическая переменная  ,
используемая
при формализации задач принятия решения, на практике, как правило, имеет
базовое терм-множество
,
используемая
при формализации задач принятия решения, на практике, как правило, имеет
базовое терм-множество 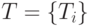 , состоящее из 2—10 термов.
Каждый терм описывается нечетким подмножеством множества значений
, состоящее из 2—10 термов.
Каждый терм описывается нечетким подмножеством множества значений  некоторой
базовой переменной
некоторой
базовой переменной  и рассматривается как лингвистическое
значение
и рассматривается как лингвистическое
значение  .
Предполагается, что объединение всех этих элементов терм-множества покрывает
полностью
.
Предполагается, что объединение всех этих элементов терм-множества покрывает
полностью  . Это гарантирует, что любой элемент
. Это гарантирует, что любой элемент  описывается
некоторым
описывается
некоторым 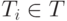 .
.
Существует способ построения частотных оценок 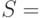 {"редко",
"часто", "иногда",...}, который основан на
предположении о том,
что слово
{"редко",
"часто", "иногда",...}, который основан на
предположении о том,
что слово 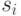 употребляется человеком не для обозначения
зарегистрированной
частоты появления факта, а для обозначения относительного числа событий в
прошлой
деятельности человека, когда рассматривалась такая же частота. Каждому
употребляется человеком не для обозначения
зарегистрированной
частоты появления факта, а для обозначения относительного числа событий в
прошлой
деятельности человека, когда рассматривалась такая же частота. Каждому 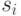 ставится в соответствие нечеткое подмножество интервала
ставится в соответствие нечеткое подмножество интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) .
Функции
принадлежности
.
Функции
принадлежности 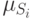 получаются на основании
психологического
эксперимента следующим образом: группе испытуемых предъявляется набор
стимулов (оценок частоты) и шкала из
получаются на основании
психологического
эксперимента следующим образом: группе испытуемых предъявляется набор
стимулов (оценок частоты) и шкала из  категорий, упорядоченных
по степени
интенсивности частоты от наименьшей
категорий, упорядоченных
по степени
интенсивности частоты от наименьшей  до наибольшей
до наибольшей  ; испытуемым
предлагается разбить стимулы на
; испытуемым
предлагается разбить стимулы на  классов согласно интенсивности
частоты,
независимо оценивая каждый стимул и помещая в любую категорию любое число
стимулов.
Каждому числу
классов согласно интенсивности
частоты,
независимо оценивая каждый стимул и помещая в любую категорию любое число
стимулов.
Каждому числу 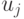 из
из ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) ,
, 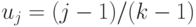 ,
ставятся в соответствие степени употребления группой испытуемых слова
,
ставятся в соответствие степени употребления группой испытуемых слова 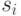 для обозначения категории. Значения функции принадлежности определяются в
результате
нормирования:
для обозначения категории. Значения функции принадлежности определяются в
результате
нормирования: ![\mu _{S_i } (u):[0,1] \to [0,1]](/sites/default/files/tex_cache/3a97487443dcd7b8ca4de69f5265d225.png) .
.
Предложенная методика оправдана следующим: выбор обозначения категории не
отражается сколь-нибудь значительно на проведении испытания. Во-первых, число
категорий (деление шкалы) не влияет кардинально на результаты эксперимента, в
котором
производится шкалирование субъективных ощущений. Во-вторых, шкала из  категорий является шкалой равно кажущихся интервалов, поскольку предполагается,
что ее деления отстоят на психологическом континууме на равных интервалах.
категорий является шкалой равно кажущихся интервалов, поскольку предполагается,
что ее деления отстоят на психологическом континууме на равных интервалах.
Естественным шагом при построении функций принадлежности элементов
терм-множества лингвистической переменной является построение одновременно
всех функций принадлежности этого терм-множества, сгруппированных в так
называемое
отношение моделирования  . Процесс построения состоит в
заполнении таблицы,
где, например, для лингвистической переменной "РАССТОЯНИЕ" столбцы
индексированы расстояниями в метрах, а строки — элементами
терм-множества "ОЧЕНЬ БЛИЗКО", "БЛИЗКО",...,
"ДАЛЕКО", "ОЧЕНЬ ДАЛЕКО".
На пересечении соответствующей строки и столбца стоит степень сходства для
испытуемого
данных понятий в определенной семантической ситуации, например, насколько
сходны понятия "БЛИЗКО" и "5 метров" в ситуации
перебегания улицы перед
быстро идущим транспортом. Расстояние берется от пешехода до машины и в данном
случае
является синонимом опасности. Вообще говоря, каждую клеточку таблицы можно
заполнять
отдельно, а потом, переставляя строки и столбцы, постараться сделать
строки и столбцы унимодальными. Если это удается, то исходное терм-множество
может быть использовано для построения нечеткой шкалы измерений, точками
отсчета которой являются сами элементы терм-множества. Перевод в эту шкалу
будет осуществляться с помощью минимаксного умножения строки, задающей исходную
лингвистическую переменную в шкале метров, на отношение моделирования.
Отношение
сходства между элементами терм-множества
. Процесс построения состоит в
заполнении таблицы,
где, например, для лингвистической переменной "РАССТОЯНИЕ" столбцы
индексированы расстояниями в метрах, а строки — элементами
терм-множества "ОЧЕНЬ БЛИЗКО", "БЛИЗКО",...,
"ДАЛЕКО", "ОЧЕНЬ ДАЛЕКО".
На пересечении соответствующей строки и столбца стоит степень сходства для
испытуемого
данных понятий в определенной семантической ситуации, например, насколько
сходны понятия "БЛИЗКО" и "5 метров" в ситуации
перебегания улицы перед
быстро идущим транспортом. Расстояние берется от пешехода до машины и в данном
случае
является синонимом опасности. Вообще говоря, каждую клеточку таблицы можно
заполнять
отдельно, а потом, переставляя строки и столбцы, постараться сделать
строки и столбцы унимодальными. Если это удается, то исходное терм-множество
может быть использовано для построения нечеткой шкалы измерений, точками
отсчета которой являются сами элементы терм-множества. Перевод в эту шкалу
будет осуществляться с помощью минимаксного умножения строки, задающей исходную
лингвистическую переменную в шкале метров, на отношение моделирования.
Отношение
сходства между элементами терм-множества 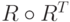 , полученное
с помощью умножения
матрицы
, полученное
с помощью умножения
матрицы  на транспонированную, задает набор функций
принадлежности элементов
лингвистической шкалы в самой шкале, а отношение
на транспонированную, задает набор функций
принадлежности элементов
лингвистической шкалы в самой шкале, а отношение 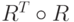 задает набор
функций принадлежности расстояний в метрах в метрической шкале.
задает набор
функций принадлежности расстояний в метрах в метрической шкале.
