Нечеткие множества как способы формализации нечеткости

Принцип обобщения

Принцип обобщения как одна из основных идей теории нечетких множеств носит эвристический характер и позволяет расширить область определения исходного отображения на класс нечетких множеств. Пусть — заданное отображение, и — нечеткое множество, заданное в . Тогда образ нечеткого множества при отображении есть нечеткое множество , заданное в с функцией принадлежности

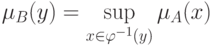
Виды области значений функции принадлежности

Все нечеткие объекты можно классифицировать по виду области значений функции принадлежности. Помимо интервала , функция принадлежности может принимать свои значения в интервале , на числовой прямой , а также в различных множествах, наделенных некой структурой.

Исторически первым обобщением понятия нечеткого множества стали -нечеткие множества, т.е. множества, у которых функции принадлежности принимают свои значения в конечной или бесконечной дистрибутивной решетке .

Важным практическим приложением для формулировки качественных представлений и оценок человека в процессе решения задачи служит случай -нечетких множеств, где — конечное линейно упорядоченное множество. Например, это может быть набор значений лингвистической переменной "КАЧЕСТВО" {"плохое", "среднее", "хорошее", "отличное"}.

Гетерогенные нечеткие множества

В том случае, когда набор нечетких множест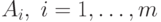в в соответствует различным свойствам рассматриваемого объекта, каждый элемент 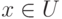характеризуется вектором значений принадлежности , выражающим степень соответствия этим свойствам. Таким образом, строится функция , где — полная решетка.

Дальнейшим обобщением понятия нечеткого множества является понятие гетерогенного нечеткого множества. По признаку однородности/неоднородности области значений функции принадлежности все описанные выше виды нечетких множеств являются гомогенными в том смысле, что одна и та же структура области значений функции принадлежности берется при оценке всех элементов универсального множества . Если же допустить, что на различных элементах универсального множества функция принадлежности может принимать свои значения из различных наиболее подходящих математических структур, то мы приходим к понятию гетерогенного нечеткого множества.

Гетерогенные нечеткие множества и связанные с ними составные лингвистические переменные высокого порядка позволяют моделировать ситуации многокритериального принятия решения, когда имеются признаки как с количественными, так и с порядковыми шкалами.