Описание синтаксиса

2.4. Описание абстрактного синтаксиса

Синтаксис, который мы изучали в этой лекции, задавал конкретный синтаксис программы со всеми ее ключевыми словами, ограничителями и прочими деталями, которые играют важную синтаксическую роль, позволяя избежать двусмысленностей, но не несут никакой семантики. Ранее мы встречались с абстрактным синтаксисом, в котором эти детали отсутствовали, оставляя только те элементы, что несут за собой смысл.

Мы видели, как описать результирующую синтаксическую структуру, используя АСД (Абстрактное Синтаксическое Дерево), такое как ранее показанное дерево, задающее синтаксис нашего класса Preview1.

Рис. 2.3. Абстрактное синтаксическое дерево

Как отмечалось, проще построить конкретное синтаксическое дерево, содержащее все символы исходного текста. Некоторые компиляторы так и поступают, но обычно в этом нет необходимости. Для последующих фаз компиляции, таких как семантический анализ, генерация кода и его оптимизация, синтаксические маркеры не играют роли. Все, что нужно для представления структуры программы, в точности содержится в АСД.

Если бы нашей целью было описание абстрактного синтаксиса, без обращения к конкретному синтаксису, то нужды в новом формализме не было бы. Вполне достаточно использовать БНФ, опуская все лексемы, не являющиеся категориями лексической грамматики, в частности, опуская ключевые слова. Для последней продукции, специфицирующей Compound, точку с запятой можно было бы опустить, оставив просто Instruction Compound.

В таких приложениях, как синтаксический анализ и компиляция исходных текстов, эта грамматика не принесла бы пользы, поскольку, очевидно, здесь требуется конкретная грамматика, обсуждаемая до сих пор. Но она может играть свою роль, помогая в изучении тех структурных свойств текстов, которые не зависят от деталей внешнего вида этих текстов.

2.5. Превращение грамматики в анализатор

Одно из приложений БНФ, как отмечалось, в том, что грамматика является руководством для построения компилятора, начиная с фазы синтаксического анализа. Компиляторы, обычно являются синтаксически управляемыми: анализатор создает АСД, а последующие фазы компиляции продолжают работать на этой структуре данных, добавляя семантическую информацию (этот процесс называется декорированием дерева).

Детальное рассмотрение процесса построения синтаксически управляемого компилятора или просто анализатора выходит за пределы данного курса. При желании можно познакомиться с идеями применяемых методов, изучая библиотеку EiffelParse. В этой библиотеке реализован не самый эффективный механизм разбора, но ее методы представляют понятную и практическую иллюстрацию применения ОО-принципов этой книги для построения анализатора и компилятора. Сам Eiffel использует более традиционные подходы разбора, с которыми можно ознакомиться, изучая библиотеку "GOBO".

Идея, стоящая за EiffelParse, состоит в том, чтобы строить нужные классы непосредственно по грамматике БНФ-Е. Для каждой категории грамматики строится небольшой класс, являющийся наследником одного из классов библиотеки EiffelParse: AGGREGATE, CHOICE, REPETITION (соответственно для продукций "Конкатенация", "Выбор" и "Повторение"). Например, для конкатенации класс будет просто перечислять различные компоненты, стоящие в правой части продукции, связывая каждую компоненту с классом, подобным образом описывающим конструкцию. Следует быть внимательным, имея дело с левой рекурсией, но в остальном классы являются зеркальным отражением продукций БНФ-Е. Транслятор YOOC, разработанный Кристиной Мингинс, создает классы непосредственно по грамматике.

Для разбора входного текста достаточно вызвать EiffelParse – процедуру parse для соответствующей категории. В результате для нее будет создано АСД. Затем можно добавить семантическую обработку любого типа, используя методы синтаксического класса. Этот подход демонстрирует мощь и элегантность ОО-моделирования процесса анализа и компиляции языка программирования.

2.6. Лексический уровень и регулярные автоматы

Для терминальных конструкций, таких как идентификаторы и числа, БНФ не создает продукций, возлагая их спецификацию на лексический уровень. По этой причине терминальные категории называются также лексическими категориями. Их спецификация появляется в "лексической грамматике", дополняющей БНФ-грамматику.

Лексические категории в БНФ

На синтаксическом уровне, покрываемом БНФ, лексемы (терминалы и ограничители) являются атомами. На лексическом уровне нас интересует внутренняя структура этих атомов. Например (используя соглашения Eiffel):

• идентификатор – это последовательность символов, первый из которых является буквой (в верхнем или нижнем регистре), а остальные могут быть буквами, цифрами или знаком подчеркивания "_";
• целое – это последовательность десятичных цифр (0-9), которые также могут содержать подчеркивание при разделении групп цифр в больших числах для облегчения чтения: 123_456_789;
• целочисленная_ константа (целое_со_знаком) – это целое, с возможно предшествующим знаком + или -.

Такие категории нетрудно выразить через БНФ (упражнение попросит вас проделать это). Но для таких простых конструкций обычно используют специфические лексические приемы, к изучению которых мы приступаем. Это позволяет избежать перегрузки грамматики продукциями для базисных структур, которые могут быть описаны более просто, и резервировать БНФ-грамматику для спецификации структур языка более высокого уровня, допускающих, в частности, вложенность.

Регулярные грамматики

Для определения структуры лексических категорий, таких как в вышеприведенных примерах, мы можем использовать регулярную грамматику – упрощенную версию БНФ.

Нетерминалами такой грамматики являются категории, подобные идентификаторам и целым, которые выступают в роли терминалов в БНФ. Для задания их структуры регулярная грамматика имеет собственные терминалы, обычно символы, принадлежащие некоторым категориям, например:

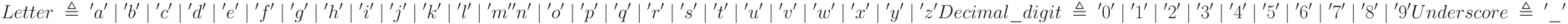
Каждая категория выражается как выбор между единичными символами, показанными в одинарных кавычках. Такие категории являются по-настоящему терминальными (атомарными), не подлежащими дальнейшим уточнениям. Общепринято использовать специальную нотацию для последовательно идущих символов, учитывая порядок их следования в алфавите; так что продукцию для Letter, добавив еще буквы в верхнем регистре, можно записать в виде:

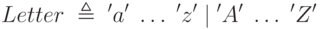
Аналогично можно определить Decimal_digit как '0'.. '9'. Регулярная грамматика может иметь те же виды продукций, что и БНФ, но со слегка отличными соглашениями и важными ограничениями:

• в продукциях "Выбор" можно использовать интервалы для задания множества символов;
• при определении лексической категории продукцией "Конкатенация" в последовательности символов не должно быть пробелов. Если вы определяете категорию как А В, то любой образец категории состоит из образца А, за которым следует без всяких разделителей образец В, никаких символов не должно быть между ними. Если языку требуется понятие разделителя, то его следует ввести явно в регулярную грамматику как лексическую категорию;
• повторение имеет упрощенную форму: если А означает ранее введенную категорию, то А* и А+ означают "ноль или более повторений А" и "один или более повторений А" соответственно. Опять-таки никаких разделителей или пробелов между образцами А не предполагается;
• никакая рекурсия, ни прямая, ни косвенная не допускается в грамматике. Простой способ выполнения этого запрета состоит в установлении порядка применения правил. Другой способ состоит в добавлении правила, согласно которому определение категории может ссылаться только на уже определенные категории.

В отличие от БНФ-Е регулярная грамматика позволяет смешивать различные виды продукций (поскольку на правила наложены существенные ограничения). Введение скобок позволяет устранить любую двусмысленность. Регулярная грамматика с учетом этих замечаний позволяет дать точные определения для рассмотренных нами лексических категорий:

Выражения, допускаемые только что определенными правилами, называются регулярными выражениями, а язык, определяемый регулярной грамматикой, – регулярным языком. Отметим следующее свойство.

Теорема: "Каноническая форма регулярного языка"

Доказательство следует из запрета рекурсивных определений. Как обсуждалось выше, любой появляющийся в правой части нетерминал определен в предыдущих правилах, поэтому вместо него можно подставить его определение. Понятно, что первое правило в такой грамматике содержит только терминалы в правой части, а в остальных правилах нетерминалы могут быть исключены, что и доказывает наше утверждение.

Например:

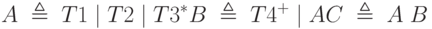
Применяя процесс, описанный при доказательстве теоремы, можно построить эквивалентную грамматику, порождающую тот же язык.

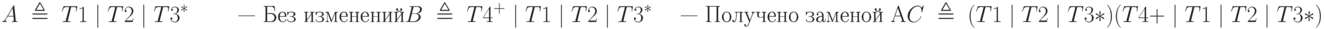
Возможно, грамматика не стала более понятной, но свойство исключения нетерминалов в ней выполняется. Аналогично доказывается более сильное утверждение: любой регулярный язык может быть задан одним регулярным выражением. В нашем примере таковым является описание категории С, рассматриваемой как начальный символ грамматики.

Теорема высвечивает принципиальное ограничение регулярных языков: они не поддерживают рекурсивную вложенность. Мы видели, что язык программирования, подобный Eiffel, содержит условный оператор, где в качестве выполняемого оператора может быть любой оператор – условный оператор, оператор цикла и любой другой с неограниченной глубиной вложенности. В БНФ можно описать такие ситуации благодаря рекурсивно определяемым продукциям; с регулярными грамматиками этого сделать нельзя.

Зато регулярные грамматики удобны для задания правил описания лексем – первичных элементов языка. Когда нужно описать лексему, состоящую из одного или нескольких символов одного вида, за которыми следует один из трех специальных символов, за которым возможно следует последовательность символов еще одного вида, для таких ситуаций регулярная грамматика – то, что требуется.

Конечные автоматы

За кулисами регулярных выражений стоит математическая теория конечных автоматов. Для первого знакомства с этой теорией, о которой можно многое сказать, удобно воспользоваться визуальной иллюстрацией конечного автомата. Конечный автомат – это граф, с узлами, представляющими состояния автомата, и дугами, помеченными элементами некоторого базисного конечного множества. В нашем примере элементы представляют терминальные символы и имена категорий.

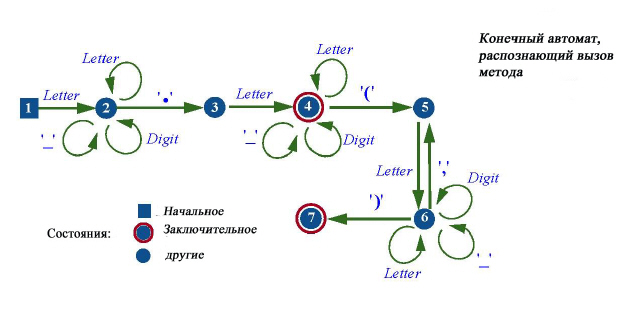
Следующий пример задает синтаксическую структуру квалифицированного вызова метода в Eiffel с возможными аргументами, подобно вызову Line8.extend(new_station):

Рис. 2.4. Конечный автомат, распознающий вызов метода

Конечный автомат можно рассматривать как машину, обрабатывающую входную строку символ за символом. Процесс начинается в узле, задающем начальное состояние, затем продолжается, следуя выходящим из узла дугам, если таковые дуги имеются. Из выходящих дуг выбирается та, которая помечена очередным символом входной строки. Следуя дуге, попадаем в узел автомата, в который ведет выбранная дуга. Это называется переходом из одного состояния в другое. На входе x9.f_g(a,a), наш автомат стартует в состоянии 1, входной символ x станет причиной перехода в состояние 2, затем 9 станет причиной перехода в то же самое состояние 2. Символ "точка" переведет автомат в состояние 3, f переведет в 4, подчеркивание и g оставят в 4. Появление круглой открывающей скобки переведет автомат в состояние 5, из которого автомат, обрабатывая список аргументов, будет переходить в состояние 6 и снова возвращаться в 5. Появление закрывающей скобки переведет автомат в заключительное состояние 7, у которого нет выходящих дуг.

Язык, распознаваемый конечным автоматом, – это множество всех строк, на которых автомат, начиная работать в начальном состоянии, переходит в конечное состояние, полностью прочитав строку. Строки Line8.extend (new_station) и x9.f_g(a, a) принимаются нашим автоматом и принадлежат языку, им распознаваемому. Строки не принадлежат языку автомата, если:

• автомат достиг состояния, в котором нет дуги, соответствующей следующему входному символу. Для нашего автомата такой может быть строка a.b.c (допустимая в Eiffel, но не допускаемая рассматриваемым автоматом); обработав начальную часть строки a.b, автомат перейдет в состояние 4 и остановится, поскольку в этом состоянии нет дуги, помеченной точкой – очередным символом строки. Заметьте, что отказ будет верен и для заключительного состояния, если входная строка не обработана полностью, например, для строки x.f(a),a;
• обработаны все символы входной строки, но автомат не достиг конечного состояния. Примером является строка a, приводящая в состояние 2, которое не является заключительным.

Основная теорема, связывающая регулярные языки и конечные автоматы, утверждает, что любой язык, заданный регулярной грамматикой, распознается конечным автоматом. Верно и обратное утверждение, что доказывает эквивалентность регулярных языков и языков, распознаваемых конечными автоматами. Не доказывая эту теорему, проиллюстрируем ее, построив для нашего автомата регулярную грамматику с языком, определяемым последней категорией:

Вызовы методов, распознаваемые этой грамматикой, являются подмножеством возможных в Eiffel вызовов, где выражения для аргументов допускают, подобно операторам, вложенность, как в вызове x.f(y.h(z.i)). Вышеприведенная лексическая грамматика и связанный с ней конечный автомат не распознают такие вызовы, поскольку аргумент для них может быть только идентификатором. Как только мы выходим за пределы лексем, так сразу требуется вся мощь БНФ. Заметьте, соглашение БНФ-Е для Повторения, включающее возможность появления разделителя, делает более удобным определение категории Argument_list, позволяя определить эту категорию одной продукцией, в правой части которой стоит {Identifier "," …}+.

Конечные автоматы обеспечивают основу создания лексических анализаторов, часть компилятора, ответственную за распознавание лексем. Фактически, не представляет особого труда определить конечный автомат по регулярной грамматике, а затем по этому определению построить непосредственно программу, распознающую лексемы. Такая схема используется в лексических анализаторах.