Хэш-таблицы, стеки, очереди
7.1. Хеш-таблицы
Массивы представляют структуры, индексированные целыми числами. Что, если нам нужны другие виды ключей? Строки являются типичным примером. Нам могут понадобиться контейнеры, в которых критерием доступа является строка символов, такие как:
- каталог персон – контейнер, в котором каждый объект содержит информацию о персоне. Вам необходимо получать информацию, задавая имя персоны;
- коллекция веб-страниц, сопровождаемая поисковой машиной; страницы индексируются всеми ключевыми словами, появляющимися на этой странице.
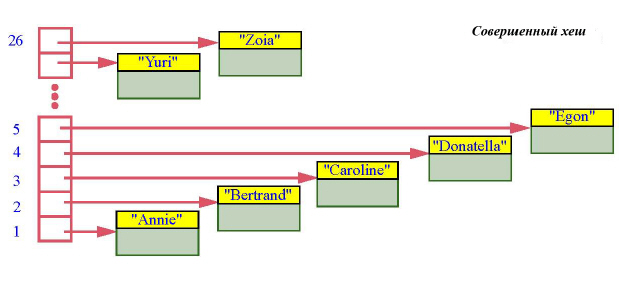
Предположим на минуту, что в первом случае все персоны, собранные в каталоге, имеют имена, отличающиеся первой буквой: Annie, Bertrand, Caroline … Тогда можно было бы использовать массив из 26 элементов, где индекс соответствовал бы коду буквы: 1 – для А, 2 – для В и так далее.
Мы хешировали ключи (строки, представляющие имена) в целые числа из интервала 1...26. "Хеширование" понимается здесь по аналогии с приготовлением котлет – мясо пропускается через мясорубку и разделяется на порции. Более точно:
Определение: хеш-функция
Другими словами, для любого key ? K функция дает значение i = h(key), такое, что a ? i ? b.
На практике обычно интервал задается в форме 0… capacity – 1 для некоторого целого capacity. Хеш-функция h(key) задается в форме f(key) Mod(capacity) (по модулю емкости контейнера), где функция f возвращает целочисленное значение, приводимое к нужному интервалу взятием по модулю. Массив, применяемый для хранения данных, имеет размерность capacity.
В нашем примере используется примитивная хеш-функция, возвращающая порядок в алфавите первой буквы имени. Слегка более сложной хеш-функцией является функция, которая суммирует все ASCII-коды символов, входящих в имя, а затем возвращает остаток при целочисленном делении полученного значения на емкость контейнера – capacity.
Хеш-функция зависит только от ключей, а не от числа элементов, так что если count – это размерность нашей задачи, то время, затрачиваемое на вычисление функции, есть O(1) или O(l), если учитывается длина ключа – l, но можно предположить, что хеш-функция использует только первые K символов ключа, где К – константа.
Предположение, что в нашем примере все имена различаются по первой букве, приводит к тому, что хеш-функция для различных имен дает различные значения. В общем случае хеш-функция называется совершенной, если для разных значений ключа она вырабатывает разные значения. Для совершенной хеш-функции вставка и поиск требуют O(1) времени.
В большинстве случаев мы не можем получить совершенную хеш-функцию, даже с описанной выше функцией, вычисляющей сумму кодов всех символов. Для несовершенных функций встречаются коллизии, когда разные ключи дают одно и то же значение функции. Хорошая хеш-функция характеризуется небольшим числом коллизий. Можно сказать, что функция, вычисляющая сумму кодов с последующим приведением по модулю емкости контейнера, лучше, чем функция, учитывающая только первую букву ключа. Для первой функции коллизии начнут фактически возникать, когда число элементов будет превосходить емкость контейнера capacity. Реализация хеш-функций должна уметь справляться с коллизиями.
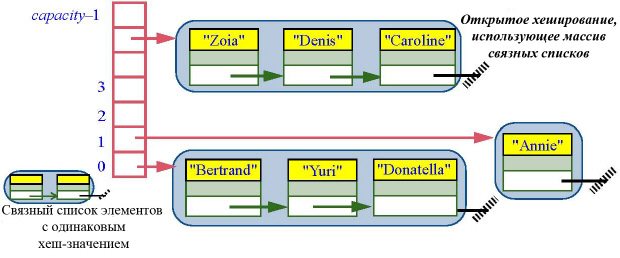
Одним из методов является так называемое открытое хеширование, когда массив комбинируется со связным списком. На последнем приведенном рисунке с совершенным хешированием массив непосредственно содержит все элементы и мог быть объявлен как
ARRAY[G]
При открытом хешировании мы могли бы использовать массив, элементами которого были бы связные списки:
ARRAY[LINKED_LIST[G]]
Каждый элемент массива с индексом i представляет список объектов, для которых хеш-функция дает значение i:
При поиске или вставке элемента в хеш-таблицу с открытым хешированием первым делом ключ преобразуется в индекс, дающий вход в список, а затем производится последовательный просмотр списка. Первая операция имеет стоимость O(1), а вторая – O(c), где c – фактор коллизии – среднее число ключей, хешируемых на данный индекс. Если емкость массива capacity считать константой, то значение с для больших count и хорошо распределенной хеш-функции будет O(count/ capacity), а с учетом нашего предположения – O(count). Чтобы избежать линейной зависимости, необходимо периодически перестраивать массив, но тогда лучше использовать другую технику, называемую закрытым хешированием.
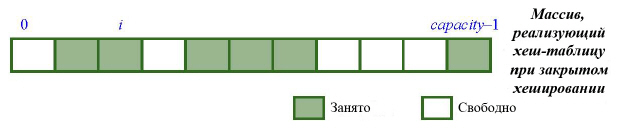
Закрытое хеширование, применяемое в классе HASH_TABLE библиотеки EiffelBase, не использует связных списков, а работает с массивом ARRAY[G]. В любой момент времени некоторые его позиции заняты, а некоторые – свободны:
Если при вставке хеш-функция вырабатывает уже занятую позицию, например, i, как показано на следующем рисунке, то применяемый механизм последовательно будет испытывать другие позиции – i1, i2, i3, пока не найдет свободную ячейку:
Общий прием состоит в следующем: если хеш-функция вырабатывает позицию для первого кандидата i = f(key) Mod(capacity), то последующие позиции определяются как i + increment, i +2 * increment, i +3 * increment и так далее, все по модулю capacity. Величина increment вычисляется как f(key) Mod (capacity -1). Такой алгоритм используется в классе HASH_TABLE библиотеки EiffelBase (смотри метод search_for_insertion для изучения деталей).
Гарантирование завершения процесса поиска означает, что цикл имеет вариант и алгоритм всегда способен найти пустую ячейку. Это достигается подходящим подбором параметров и политикой перестройки массива при его заполнении. Фактически, мы не ждем до последней минуты, – перераспределение начинается, когда коэффициент заполнения достигает граничного значения – 80% в классе HASH_TABLE.
Поразительно, но такая политика в сочетании с хорошим выбором хеш-функции приводит к тому, что практически вставка и поиск требуют O(1) затрат (смотри ссылку в конце этой лекции на теоретический анализ сложности).
Такое поведение означает, что для практических целей хеш-таблицы почти так же хороши, как и массивы, но позволяют иметь произвольные ключи, так что хеш-таблицу с элементами, идентифицируемыми строковым ключом, можно рассматривать как массив, индексируемый строками, а не целыми.
 , что примерно дает 8 миллиардов значений. Даже если не учитывать проблемы с памятью, было бы абсурдно воспринимать всерьез такие массивы, когда на практике приходится иметь дело с множествами существенно меньшего размера. При хешировании памяти выделяется чуть больше, чем фактически необходимо, но вместе с тем достигается поведение, сравнимое с поведением массива.
, что примерно дает 8 миллиардов значений. Даже если не учитывать проблемы с памятью, было бы абсурдно воспринимать всерьез такие массивы, когда на практике приходится иметь дело с множествами существенно меньшего размера. При хешировании памяти выделяется чуть больше, чем фактически необходимо, но вместе с тем достигается поведение, сравнимое с поведением массива.Нахождение хеш-функций, приводящих к такому эффективному поведению, является в некотором роде искусством. Образцом и источником вашего вдохновения может послужить функция, используемая в классе HASH_TABLE.
Класс HASH_TABLE[G, KEY] является первым примером, где появляются два родовых параметра типа, а не один, как было ранее: G задает тип элементов, а KEY – тип ключей этих элементов. Этот класс можно использовать, например, для хранения объектов, которые представляют персоны, идентифицируемые именами:
personnel_directory: HASH_TABLE [PERSON, STRING ]
У этого класса есть несколько фундаментальных методов. Класс имеет единственную процедуру создания make. Для создания хеш-таблицы можно применить вызов:
create personnel_directory.make (initial_size)
Здесь initial_size – это некоторое положительное целое. Не имеет большого значения, каким его выбрать. Как следует из его названия, это просто некоторая подсказка для начального выделения памяти. Если вы зададите число много ниже реальной потребности, то это приведет во время выполнения к нескольким дополнительным перестройкам массива.
Рассмотрим запросы, существующие в классе. Чтобы узнать, есть ли в классе элемент с заданным ключом, используйте запрос
has (k: KEY ): BOOLEAN
Для получения элемента, ассоциированного с заданным ключом, если таковой есть:
item (k: KEY ) alias "[]": G assign put
— Элемент, ассоциированный с заданным ключом, если таковой есть,
— в противном случае – значение по умолчанию для типа G
ensure
default_value_if_not_present:
not (has (k)) implies (Result = computed_default_value)
Постусловие показывает, что если нет элемента с заданным ключом, то результатом является значение по умолчанию типа G (ноль для целых, false – для булевских, void – для ссылок). Это не лучший способ тестирования наличия элемента в таблице, так как там может существовать элемент, имеющий значение по умолчанию, так что предварительно стоит использовать запрос has в таких ситуациях.
Спецификация alias "[]" показывает, что так же, как и для элементов массива, возможно применение квадратных скобок для элементов хеш-таблиц, что позволяет писать:
personnel_directory ["Isabelle"]
Эта запись является синонимом:
personnel_directory.item ("Isabelle")
Форма с квадратными скобками короче и привычнее, так что она будет использоваться в дальнейшем.
Для вставки элемента в таблицу нужно задать как сам элемент, так и его ключ:
personnel_directory.put (that_person, "Isabelle") [8]
Листинг
7.8.
Это справедливо и тогда, когда ключ является атрибутом элемента:
personnel_directory.put (that_person, that_person.name)
Класс предлагает четыре операции вставки с одной и той же сигнатурой:
put (new: G; k: KEY ) — Команда-присваиватель для элемента.
forse (new: G; k: KEY )
extend (new: G; k: KEY )
require
not_present: not has (k)
replace (new: G; k: KEY )
Среди них extend имеет предусловие, устанавливающее применимость только тогда, когда элемента с заданным ключом нет в таблице; остальные три всегда применимы. Предложение "note" в начале класса объясняет, когда следует использовать тот или иной вариант. Я воспроизведу его здесь, опуская некоторые детали.
Варианты вставки в хеш-таблицы (из текста класса HASH_TABLE)
- Используйте put, если вы хотите, чтобы вставка происходила только тогда, когда в таблице нет элемента с данным ключом, в противном случае ничего делаться не будет.
- Используйте force, если вы хотите делать вставку в любом случае. Это означает, что существующий элемент с данным ключом будет удален.
- Используйте extend, если вы уверены, что в таблице нет элемента с заданным ключом, – это обеспечит более быструю вставку.
- Используйте replace, если вы хотите заменить существующий элемент с заданным ключом, ничего не делая в противном случае.
В первых двух случаях процедура будет устанавливать значение булевского запроса found, позволяющего узнать после вставки, был ли уже в таблице элемент с заданным ключом.
Объявление элемента с заданием псевдонима и команды-присваивателя выглядит так:
item (k: KEY ) alias "[]": G assign put
В результате доступна скобочная нотация, позволяющая вставлять элементы в хеш-таблицу, применяя инструкцию, подобную присваиванию:
personnel_directory ["Isabelle"]:= that_person
Фактически, это краткая форма записи вызова put, более простая, чем рассмотренная в примере 7.8 . Для удаления элемента с заданным ключом используйте:
remove (k: KEY )
Команда не имеет эффекта, если элемента с заданным ключом в таблице нет. Выяснить, что фактически происходило, может запрос removed.
Для удаления всех элементов служит процедура clear_all.
Выполняя эти операции, нет необходимости заботиться о размере структуры данных. Благодаря перестраиваемым массивам Eiffel, сами методы заботятся о выделении достаточного пространства для всех текущих элементов.
Вот обзор стоимости операций хеш-таблицы.
| Операция | Метод класса HASH_TABLE | Сложность |
|---|---|---|
| Доступ по ключу | item, has | O(1) |
| Вставка по ключу | put, force, extend | O(count) |
| Замена по ключу | replace | O(1) |
| Удаление по ключу | remove | O(1) |
При работе с большими системами с большим числом объектов вы обнаружите, что хеш-таблицы станут одним из ваших любимых инструментов.