Описание синтаксиса
2.3. Использование БНФ
Все, что нужно знать о БНФ, уже сказано. Для эффективного использования этого метода описания языков рассмотрим некоторые прагматические наблюдения.
Применение БНФ
- понять синтаксис существующих языков (не только языков программирования);
- определить синтаксис языка, который предстоит спроектировать;
- написать синтаксический анализатор – парсер (parser).
Второе применение не столь фантастично, как кажется с первого взгляда. Возможно, вам еще не скоро придется проектировать язык общецелевого применения – соперник таких языков, как С#, Java или Eiffel. Но программистам довольно часто приходится иметь дело с "малыми" языками. Всякий раз, когда приходится обрабатывать данные сложного формата, эти данные можно рассматривать как предложения некоторого языка, синтаксис которого удобно задать, используя БНФ. Упражнения этой лекции потребуют от вас выполнения подобной работы.
Третье приложение (построение анализатора) полезно при написании компиляторов и других инструментов, предназначенных для обработки программ, а в более общем случае – структурированных текстов. Одна из первых задач для таких инструментов – это реконструкция структуры текста в форме абстрактного синтаксического дерева. Это работа анализатора, как мы увидим в следующей лекции. Любому анализатору необходимо формальное описание синтаксиса языка – он может получить его из БНФ-грамматики.
Язык, порождаемый грамматикой
БНФ-грамматику можно рассматривать двумя дополняющими способами, вытекающими из двух предложений в определении понятия грамматики.
- Это механизм распознавания, позволяющий определить, является ли некоторая последовательность из терминальных образцов и ограничителей фразой нашего языка, и, если это так, восстановить ее синтаксическую структуру. Эта точка зрения на грамматику полезна при написании анализатора.
- Грамматика является также порождающим механизмом: применяя ее правила, можно сгенерировать все фразы языка, одну за другой.
Вторая точка зрения на практике менее полезна, но в то же время важна. Давайте исследуем ее немного глубже. Для порождения всех возможных образцов любого нетерминала – в частности, начального (или, что то же, вершинного) символа грамматики – достаточно анализировать продукцию, определяющую этот символ (напомним, что в БНФ-Е такая продукция единственная).
Эти четыре механизма порождения предложений применяйте до тех пор, пока хоть одно из них будет применимо. В конечном счете будут порождены все предложения языка. Процесс этот обычно не завершается, поскольку, как мы видели, языки, представляющие интерес на практике, являются бесконечными.
Применяя этот процесс к нетерминалу А, чья продукция использует В, возможно, придется применять те же правила – на шагах Р3 и Р4 – к другим категориям.
Рекурсивные грамматики
Последнее наблюдение может вызывать некоторое опасение. Что, если, применяя процесс к А, мы должны будем применить его к В, а это приведет к тому, что мы снова встретим А? Продукция для составного оператора является хорошим примером:

Определение включает категорию Instruction, продукция для которой включает категорию 
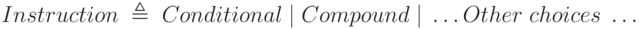
Заметьте, что и определение категории Conditional включает категорию Compound. Если попытаться понять структуру Compound, разыскивая его образцы путем применения вышеприведенных правил, то кажется, что мы впадем в цикл – вывод, не имеющий смысла.
Определение понятия, в котором явно или неявно понятие определяется через само себя, называется рекурсивным. Рекурсия – использование рекурсивных определений – самая популярная вещь во всех областях программирования, и мы посвятим ей отдельную лекцию. Но уже здесь, где нет практически полезных грамматик, не использующих рекурсию, мы убедимся в важности рекурсивных грамматик.
Начнем изучение с небольшого примера. Рассмотрим мини-язык с тремя ключевыми словами heads, tails, stop (головы, хвосты и остановка). Других терминалов в этом языке не будет. Начальным нетерминалом будет категория Game, и вся грамматика задается тремя продукциями – выбором и двумя конкатенациями:

Ситуация напоминает ситуацию с категориями Conditional, Instruction, Compound, определяемыми друг через друга.
Время теста!
Из-за рекурсии грамматика может показаться бессмысленной. Но будем прагматиками и спросим себя, нельзя ли использовать грамматику для генерирования образцов, применяя описанный выше процесс. Заметим, что в продукции для Game одна из ветвей, stop, является терминальной, что позволяет сгенерировать первое предложение (образец Game):
- stop
Но теперь мы можем использовать полученную информацию для генерирования образцов Head_start и Tail_start, определяемых через Game. Соответствующие продукции скажут нам, что heads stop является образцом Head_start, а tails stop – образцом Tail_start. Воспользуемся этими образцами в продукции для Game, получим два новых образца:
- heads stop
- tails stop
Получив эти образцы, и применяя тот же процесс, можно получить следующее множество образцов:
- heads heads stop
- heads tails stop
- tails heads stop
- tails tails stop
Этот процесс удвоения образцов можно продолжать. Становится понятным и общая конструкция образца Game: он представляет последовательность "голов" и "хвостов", идущих в произвольном порядке, она заканчивается терминалом stop. Нетрудно доказать, что любая такая последовательность является образцом. Немного сложнее доказательство того, что образцов другого вида для Game нет.
Очень простой язык этой грамматики с начальным нетерминалом Game можно рассматривать как все последовательности возможных исходов бросания монеты при игре в "орел или решка". Последовательность заканчивается в тот момент, когда игрок кричит stop. Этот язык можно описать и не рекурсивной грамматикой:

Грамматика задана тремя продукциями, первая из которых является конкатенацией, вторая – повторением с пустым разделителем, третья – выбором.
Применяя для генерирования языка продукционные правила, мы использовали стратегию, в которой терминалы предпочтительнее нетерминалов. Выбрав другую стратегию, можно впасть в бесконечный цикл, не сгенерировав ни единого предложения. Например, начав с первой возможности для нетерминала Game, получим Head_start, а после его замены – heads Game. Многократно применяя эту же стратегию для Game, получим последовательность, в которой всегда присутствует нетерминал Game, что не дает создать предложение языка, которое по определению состоит только из терминальных символов.
Во избежание подобных ситуаций процессу генерирования языка необходимы подходящие стратегии, или эвристики, подобные той, которая применялась для выбора – если есть ветвь, содержащая только терминалы, то выбирается такая ветвь, в противном случае выбирается продукция, начинающаяся с лексемы.
Даже при наличии таких эвристик процесс генерации не создаст ни одного предложения языка, если его грамматика полностью рекурсивна. Для запуска процесса генерации необходимо, чтобы по меньшей мере некоторые выборы включали только лексемы. Грамматики, такие как

или

бесполезны. Эти проблемы подробно будут обсуждаться в лекции, посвященной рекурсии. Более тонким случаем являются грамматики, содержащие лексемы, но являющиеся леворекурсивными, как в следующем примере:
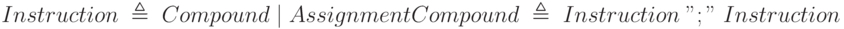
Для простоты в этой грамматике Assignment считается терминалом, определенным вне грамматики (по аналогии с лексемами, определяемыми на уровне лексического анализа). Эта грамматика имеет смысл и порождает такие предложения, как:
- assignment_1
- assignment_1; assignment_2
и так далее. Для получения конструктивного вида таких рекурсивных определений необходима общая теория, набросок которой будет дан позднее.
