Обобщенные линейные автоматы без потери информации
Теорема 16.3. Для того чтобы у ЛА  существовал подавтомат ОБПИ
существовал подавтомат ОБПИ  , где
, где  и
и 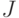 - непустые собственные подмножества множеств входных и выходных каналов ЛА соответственно, необходимо и достаточно, чтобы матрица
- непустые собственные подмножества множеств входных и выходных каналов ЛА соответственно, необходимо и достаточно, чтобы матрица  содержала подматрицу ранга
содержала подматрицу ранга 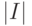 , а матрицы
, а матрицы ![[D_j], [B_j], [A_j]](/sites/default/files/tex_cache/dd4c05ad817c9cb75ad5f700298aa888.png) были ненулевыми.
были ненулевыми.
Выше уже отмечалось, что у заданного ЛА  в общем случае может существовать несколько различных подавтоматов ОБПИ
в общем случае может существовать несколько различных подавтоматов ОБПИ  . Наибольший интерес среди них представляет такой подавтомат, у которого подмножество I максимально, а подмножество
. Наибольший интерес среди них представляет такой подавтомат, у которого подмножество I максимально, а подмножество 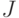 минимально по мощности. Далее такой подавтомат
минимально по мощности. Далее такой подавтомат  будем называть оптимальным ОБПИ подавтоматом ЛА
будем называть оптимальным ОБПИ подавтоматом ЛА  .
.
Содержательно оптимальный подавтомат ОБПИ  дает возможность восстанавливать информацию максимального объема, поступающую на вход ЛА
дает возможность восстанавливать информацию максимального объема, поступающую на вход ЛА  , при минимальных затратах, определяемых числом наблюдаемых выходных каналов.
, при минимальных затратах, определяемых числом наблюдаемых выходных каналов.
Восстановление фрагмента неизвестного входного слова 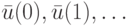 оптимального подавтомата
оптимального подавтомата  осуществляется путем последовательного решения систем линейных алгебраических уравнений
осуществляется путем последовательного решения систем линейных алгебраических уравнений

для 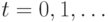 В силу теоремы 6.1 необходимым и достаточным условием разрешимости систем является условие
В силу теоремы 6.1 необходимым и достаточным условием разрешимости систем является условие 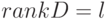 . Если
. Если  , то
, то 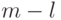 уравнений этих систем являются линейными комбинациями
уравнений этих систем являются линейными комбинациями  остальных уравнений. Последнее означает, что для упомянутого восстановления в действительности требуется наблюдать не все
остальных уравнений. Последнее означает, что для упомянутого восстановления в действительности требуется наблюдать не все  выходных каналов, а только
выходных каналов, а только  из них. По существу оставшиеся
из них. По существу оставшиеся 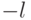 каналов являются при этом избыточными.
каналов являются при этом избыточными.
Из этих рассуждений вытекает справедливость следующего утверждения.
Теорема 16.4. Если  является оптимальным ОБПИ подавтоматом ЛА A, то
является оптимальным ОБПИ подавтоматом ЛА A, то 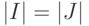 .
.
Опишем теперь способ, позволяющий для заданного ЛА найти его оптимальный подавтомат ОБПИ.
Предположим, что исходный ЛА является БПИ, причем  . Из теоремы 16.4 следует, что в нем
. Из теоремы 16.4 следует, что в нем 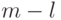 каналов при восстановлении неизвестного входного слова являются избыточными. Приведя методом Гаусса матрицу
каналов при восстановлении неизвестного входного слова являются избыточными. Приведя методом Гаусса матрицу  ЛА к ступенчатой форме, найдем избыточные каналы и исключим их из дальнейшего рассмотрения. Очевидно, что полученный при этом подавтомат является оптимальным ОБПИ подавтоматом.
ЛА к ступенчатой форме, найдем избыточные каналы и исключим их из дальнейшего рассмотрения. Очевидно, что полученный при этом подавтомат является оптимальным ОБПИ подавтоматом.
Если исходный ЛА не является автоматом БПИ, то оптимальный ОБПИ подавтомат, если таковой существует, можно найти методом перебора начиная с подавтомата 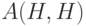 , где
, где 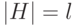 . Перебор будем осуществлять, например, следующим образом.
. Перебор будем осуществлять, например, следующим образом.
Начнем с попытки удаления у ЛА одного выходного канала  . Если удаление одного очередного канала
. Если удаление одного очередного канала  дает ОБПИ подавтомат, то он и является искомым. Если же ни один из получаемых при этом подавтоматов не является ОБПИ, необходимо перейти к удалению из ЛА всевозможных пар выходов
дает ОБПИ подавтомат, то он и является искомым. Если же ни один из получаемых при этом подавтоматов не является ОБПИ, необходимо перейти к удалению из ЛА всевозможных пар выходов 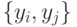 , где
, где 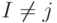 и
и 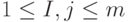 . Среди полученных на втором этапе подавтоматов может найтись ОБПИ, который и будет являться искомым оптимальным подавтоматом. Продолжим этот процесс далее аналогичным образом до тех пор, пока на очередном этапе либо не будет найден подавтомат ОБПИ, который и является искомым оптимальным ОБПИ, либо при исключении
. Среди полученных на втором этапе подавтоматов может найтись ОБПИ, который и будет являться искомым оптимальным подавтоматом. Продолжим этот процесс далее аналогичным образом до тех пор, пока на очередном этапе либо не будет найден подавтомат ОБПИ, который и является искомым оптимальным ОБПИ, либо при исключении 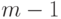 выходов (рассматриваются все возможные сочетания из
выходов (рассматриваются все возможные сочетания из 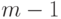 выходов) ни один подавтомат не является ОБПИ. Последнее означает отсутствие у исходного ЛА подавтоматов ОБПИ.
выходов) ни один подавтомат не является ОБПИ. Последнее означает отсутствие у исходного ЛА подавтоматов ОБПИ.
При реализации описанного способа придется обращаться к описанной ранее в этом разделе процедуре отыскания по заданному множеству 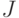 выходных каналов такого множества
выходных каналов такого множества  входных каналов, что подавтомат
входных каналов, что подавтомат  является ОБПИ. В худшем случае таких обращений будет
является ОБПИ. В худшем случае таких обращений будет 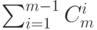 .
.
Проиллюстрируем описанный способ на примере ЛА над полем 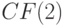 , заданного следующими характеристическими матрицами:
, заданного следующими характеристическими матрицами:
![A=
\left [
\begin {matrix}
1&0&0\\
0&0&0\\
0&0&0&
\end {matrix}
\right ],
B=
\left [
\begin {matrix}
1&0&0\\
0&1&0\\
0&0&1
\end {matrix}
\right ],
C=
\left [
\begin {matrix}
1&0&0\\
0&1&0\\
0&1&1\\
0&0&1
\end {matrix}
\right ],
D=
\left [
\begin {matrix}
0&1&0\\
1&0&0\\
0&0&0\\
1&0&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/9a4debc59401db6e0b60f5a7db229b54.png)
Поскольку для рассматриваемого ЛА 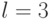 , поиск оптимального подавтомата ОБПИ начнем с анализа подавтоматов с тремя выходами. В связи с этим среди четырех выходных каналов этого ЛА необходимо исключить один.
, поиск оптимального подавтомата ОБПИ начнем с анализа подавтоматов с тремя выходами. В связи с этим среди четырех выходных каналов этого ЛА необходимо исключить один.
Заметим: в начале раздела для приведенных матриц  и
и  было установлено, что в качестве избыточного выхода может быть принят как
было установлено, что в качестве избыточного выхода может быть принят как  , так и
, так и 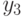 и
и 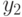 . Для определенности остановимся на первом варианте. Тогда удаление выхода
. Для определенности остановимся на первом варианте. Тогда удаление выхода  приведет к удалению из матриц
приведет к удалению из матриц  и
и  четвертой строки.
четвертой строки.
Поскольку 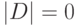 , то
, то 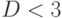 , следовательно, подавтомат с тремя выходами не является БПИ. Поэтому для поиска оптимального подавтомата ОБПИ воспользуемся перебором, организация которого была описана выше.
, следовательно, подавтомат с тремя выходами не является БПИ. Поэтому для поиска оптимального подавтомата ОБПИ воспользуемся перебором, организация которого была описана выше.
Положим 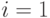 ; тогда удаление выхода
; тогда удаление выхода 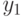 (или, что все равно, первой строки из матрицы
(или, что все равно, первой строки из матрицы  в соответствии с процедурой установления существования оптимального ОБПИ
в соответствии с процедурой установления существования оптимального ОБПИ 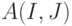 при заданном множестве
при заданном множестве 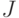 ) приводит к матрице
) приводит к матрице
![D_{y_2, y_3}=
\left [
\begin {matrix}
1&0&0\\
0&0&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/c10e7c37e7bf173f71959721064798d4.png)
Поскольку любые ее подматрицы размерности  имеют ранг, меньший 2, то условия теоремы 16.3 не выполняются и поэтому исключение выхода
имеют ранг, меньший 2, то условия теоремы 16.3 не выполняются и поэтому исключение выхода 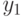 не приведет к выделению подавтомата ОБПИ с двумя входными (выходными) каналами.
не приведет к выделению подавтомата ОБПИ с двумя входными (выходными) каналами.
Положим 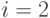 ; тогда удаление выхода
; тогда удаление выхода 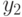 приводит к матрице
приводит к матрице
![D_{y_1, y_2}=
\left [
\begin {matrix}
0&1&0\\
0&0&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/fa40d967bf85d1983753565b3af111bf.png)
По той же причине, что и в предыдущем случае, исключение выхода 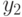 также не приведет к выделению подавтомата ОБПИ.
также не приведет к выделению подавтомата ОБПИ.
Положим 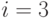 ; тогда удаление выхода
; тогда удаление выхода 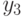 приводит к матрице
приводит к матрице
![\begin {matrix}
&&&&&u_1&u_2&u_3
\end {matrix}\\
D_{y_1, y_2}=
\left [
\begin {matrix}
\ldots&\ldots&\\
\vdots0&1&\vdots &0\\
\vdots1&0&\vdots &0\\
\ldots & \ldots &
\end {matrix}
\right ]](/sites/default/files/tex_cache/4dd02d9850f43cc0c9145edddf043015.png)
Ее подматрица, выделенная пунктиром, имеет ранг 2, следовательно, потенциально восстанавливаемыми являются компоненты 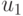 и
и 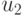 входного вектора. Поскольку удаление упомянутой подматрицы из
входного вектора. Поскольку удаление упомянутой подматрицы из  приводит к нулевой матрице, перейдем к пункту 2 упомянутой выше процедуры.
приводит к нулевой матрице, перейдем к пункту 2 упомянутой выше процедуры.
Удалив из матрицы  третью строку, соответствующую ненаблюдаемому выходу
третью строку, соответствующую ненаблюдаемому выходу 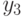 , получим матрицу
, получим матрицу
![\begin {matrix}
&&&&s_1&s_2&s_3
\end {matrix}\\
C_{y_1, y_2}=
\left [
\begin {matrix}
1&0&0\\
0&1&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/d46e0bb0e75b2908fba202af27e08c13.png)
в которой столбцы 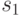 и
и 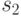 содержат ненулевые элементы. Следовательно,
содержат ненулевые элементы. Следовательно, 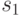 и
и 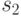 - компоненты, которые необходимы для вычисления неизвестных
- компоненты, которые необходимы для вычисления неизвестных 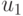 и
и 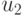 .
.
В соответствии с пунктом 3 процедуры построим матрицу ![[A_{y_1, y_2}]](/sites/default/files/tex_cache/6b29503ffe7a5c924dd5919cb1d7eda4.png) , удалив из
, удалив из  строки и столбцы с номерами 1, 2, которым соответствуют переменные
строки и столбцы с номерами 1, 2, которым соответствуют переменные 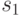 и
и 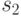
![[A_{y_1, y_2}]=[0 0]'](/sites/default/files/tex_cache/aa06905fca7c9c57fb5dbb1fa803ff89.png)
Поскольку эта матрица нулевая, то в соответствии с процедурой переходим к пункту 4. Выделим в матрице  две первые строки, соответствующие компонентам
две первые строки, соответствующие компонентам 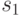 и
и 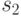 , и из полученной матрицы удалим два первых столбца, соответствующих переменным
, и из полученной матрицы удалим два первых столбца, соответствующих переменным 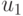 и
и 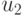 . Оставшаяся матрица
. Оставшаяся матрица
![[B_{y_1, y_2}]=[0 0]'](/sites/default/files/tex_cache/48bc473f183295df4931a0bcd29e79d1.png)
является нулевой. Построенные в процессе выполнения процедуры матрицы ![[D_{y_1, y_2}], [B_{y_1. y_2}], [A_{y_1, y_2}]](/sites/default/files/tex_cache/2d09ec09b55ed456bf660aa8a28bc4e6.png) , а также матрица
, а также матрица  заданного ЛА удовлетворяют условиям теоремы 16.3. Таким образом, подавтомат, полученный за счет удаления выхода
заданного ЛА удовлетворяют условиям теоремы 16.3. Таким образом, подавтомат, полученный за счет удаления выхода 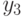 , является ОБПИ.
, является ОБПИ.
В соответствии с процедурой найденный оптимальный ОБПИ имеет следующие характеристические матрицы:
![A=
\left [
\begin {matrix}
1&0\\
0&0
\end {matrix}
\right ],
B=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ] ,
C=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ],
D=
\left [
\begin {matrix}
0&1\\
1&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/66a4c653feb1481e43f968addeb614f7.png)
Пусть, например, начальным состоянием рассматриваемого автомата является ![s(0)=[1,0,1]',](/sites/default/files/tex_cache/204477214171183da709eff248b249ad.png) а на выходе наблюдается вектор
а на выходе наблюдается вектор ![[y_1(0), y_2(0)]'=[0,1]'](/sites/default/files/tex_cache/c47e765bc9682c1021b4c3f83d682744.png) . Тогда по формуле (1.2) получаем
. Тогда по формуле (1.2) получаем
![\left [
\begin {matrix}
0\\
1
\end {matrix}
\right ]=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ]
\left [
\begin {matrix}
1\\
0
\end {matrix}
\right ]
\oplus
\left [
\begin {matrix}
0&1\\
1&0
\end {matrix}
\right ]
\left [
\begin {matrix}
u_1(0)\\
u_2(0)
\end {matrix}
\right ]](/sites/default/files/tex_cache/35bd81c95f161661cc5aaa228f2a7b84.png)
что в координатной форме дает систему
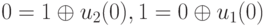
Отсюда получаем 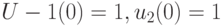 . Вычислим теперь следующее состояние подавтомата по формуле (1.1):
. Вычислим теперь следующее состояние подавтомата по формуле (1.1):
![\left [
\begin {matrix}
s_1(1)\\
s_2(1)
\end {matrix}
\right ]=
\left [
\begin {matrix}
1&0\\
0&0
\end {matrix}
\right ]
\left [
\begin {matrix}
s_1(0)\\
s_2(0)
\end {matrix}
\right ] \oplus
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ]
\left [
\begin {matrix}
u_1(0)\\
u_2(0)
\end {matrix}
\right ]](/sites/default/files/tex_cache/a3d07392f2dff21c32f5d2e6336076a9.png)
Тогда в координатной форме получаем
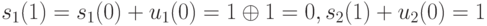
Далее по аналогии с изложенным выше для 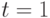 получаем систему
получаем систему
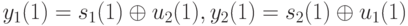
которая при наблюдаемом, например, векторе [0,1]' становится такой:
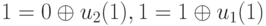
Отсюда 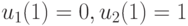 . Процесс восстановления последующих входных векторов может быть продолжен и далее аналогичным образом.
. Процесс восстановления последующих входных векторов может быть продолжен и далее аналогичным образом.
Заметим, что если у ЛА, для которого ищется оптимальный подавтомат , ОБПИ таков, что  , то этот подавтомат не единственен. В самом деле, пусть у ЛА имеются дублирующие друг друга выходы, т. е. по крайней мере один его выход является избыточным. В этом случае при исключении избыточных выходов множество неизбыточных выходов может быть разным по составу в зависимости от того, какие из дублирующих выходов оставлены и какие исключены. Отсюда следует, что такому ЛА соответствуют различные неизбыточные по выходам автоматы, отличающиеся друг от друга множествами выходных каналов. Очевидно, что построенные для них оптимальные подавтоматы ОБПИ также будут отличаться друг от друга составом выходных каналов.
, то этот подавтомат не единственен. В самом деле, пусть у ЛА имеются дублирующие друг друга выходы, т. е. по крайней мере один его выход является избыточным. В этом случае при исключении избыточных выходов множество неизбыточных выходов может быть разным по составу в зависимости от того, какие из дублирующих выходов оставлены и какие исключены. Отсюда следует, что такому ЛА соответствуют различные неизбыточные по выходам автоматы, отличающиеся друг от друга множествами выходных каналов. Очевидно, что построенные для них оптимальные подавтоматы ОБПИ также будут отличаться друг от друга составом выходных каналов.
Если заданный ЛА является неизбыточным по выходам, имеет место следующее утверждение.
Теорема 16.5. Если у неизбыточных по выходам ЛА  оптимальный подавтомат ОБПИ существует, то он единственен.
оптимальный подавтомат ОБПИ существует, то он единственен.
Доказательство. Проведем его методом от противного. Пусть для ЛА  , у которого
, у которого 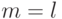 , существует два различных оптимальных подавтомата ОБПИ
, существует два различных оптимальных подавтомата ОБПИ 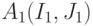 и
и 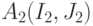 . Рассмотрим все возможные соотношения между подмножествами
. Рассмотрим все возможные соотношения между подмножествами 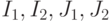 :
:
-
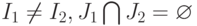 или
или 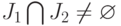 .
.В этом случае в силу оптимальности подавтоматов
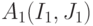 и
и 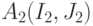 соответствующие им системы уравнений
соответствующие им системы уравнений  , из которых определяются неизвестные, сопоставляемые входным каналам подмножеств
, из которых определяются неизвестные, сопоставляемые входным каналам подмножеств 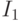 и
и  , имеют единственное решение. Объединим эти системы в одну и будем рассматривать ее как систему относительно неизвестных, сопоставляемых входным каналам множества
, имеют единственное решение. Объединим эти системы в одну и будем рассматривать ее как систему относительно неизвестных, сопоставляемых входным каналам множества 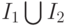 . Понятно, что последняя система также имеет единственное решение. Это означает, что у исходного ЛА существует такой подавтомат ОБПИ, который при наблюдении сигналов на каналах из множества
. Понятно, что последняя система также имеет единственное решение. Это означает, что у исходного ЛА существует такой подавтомат ОБПИ, который при наблюдении сигналов на каналах из множества  позволяет восстановить сигналы на входных каналах из множества
позволяет восстановить сигналы на входных каналах из множества 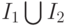 . Поскольку
. Поскольку  , то
, то 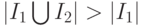 и
и 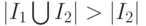 , следовательно, подавтоматы
, следовательно, подавтоматы 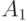 и
и 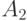 не являются оптимальными ОБПИ подавтоматами, что противоречит исходному предположению.
не являются оптимальными ОБПИ подавтоматами, что противоречит исходному предположению. -
 и
и 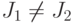 .
.Как и в предыдущем случае, объединим две упоминавшихся системы в одну и будем рассматривать ее как систему относительно неизвестных, соответствующих входным каналам множества
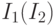 . Поскольку
. Поскольку 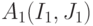 и
и 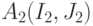 - оптимальные подавтоматы ОБПИ, ранг объединенной системы равен
- оптимальные подавтоматы ОБПИ, ранг объединенной системы равен 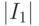 . Из теоремы 16.4 следует, что для
. Из теоремы 16.4 следует, что для 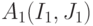 и
и 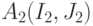 выполняются равенства
выполняются равенства  и
и  . Тогда из неравенства
. Тогда из неравенства 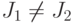 вытекает, что
вытекает, что 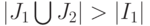 (или, что все равно,
(или, что все равно, 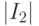 ).
).
Ввиду того что ранг матрицы  исходного ЛА равен
исходного ЛА равен  , а
, а 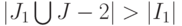 , в упомянутой объединенной системе имеется
, в упомянутой объединенной системе имеется 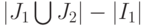 уравнений, являющихся линейными комбинациями других уравнений той же системы. Последнее означает, что исходный ЛА
уравнений, являющихся линейными комбинациями других уравнений той же системы. Последнее означает, что исходный ЛА  , у которого существует два различных оптимальных ОБПИ подавтомата, имеет избыточные выходы, что противоречит условию теоремы.
, у которого существует два различных оптимальных ОБПИ подавтомата, имеет избыточные выходы, что противоречит условию теоремы.
Из изложенного следует, что в действительности возможен лишь случай  и
и  , что и доказывает теорему.
, что и доказывает теорему.
Вопросы и упражнения
- Дайте определение избыточного выходного канала линейного автомата.
- Сформулируйте ранговый критерий отсутствия у линейного автомата избыточных выходных каналов.
- Сформулируйте тот же критерий в терминах отношений между числом входных и выходных каналов линейного автомата БПИ.
- Опишите общий метод нахождения избыточных выходных каналов ЛА.
- Сформулируйте определение обобщенного линейного автомата БПИ.
- Дайте определение обобщенного линейного подавтомата
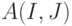 линейного автомата
линейного автомата  , где
, где  и
и 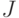 - заданные подмножества входных и выходных каналов автомата
- заданные подмножества входных и выходных каналов автомата  .
. - Опишите процедуру построения обобщенного линейного подавтомата
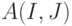 .
. - Сформулируйте необходимые и достаточные условия существования обобщенного линейного подавтомата
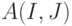 .
. - Дайте определение оптимального обобщенного линейного подавтомата
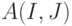 линейного автомата
линейного автомата  .
. - В случае существования у ЛА оптимального обобщенного линейного подавтомата
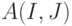 является ли такой подавтомат единственным?
является ли такой подавтомат единственным?
