Синтез экспериментов методами динамического программирования
Синтез синхронизирующей последовательности
Решение задачи синтеза СП, минимальной по весу, будет состоять из двух этапов, первый из которых заключается в построении по таблице переходов-выходов автомата Мили графа, который будет именоваться графом синхронизации автомата (ГСА), а второй - в поиске в нем минимальной по весу СП методом динамического программирования .
Построение ГСА осуществляется рекурсивно. Вначале в число его вершин включается вершина 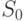 , соответствующая множеству допустимых начальных состояний автомата. Вершину
, соответствующая множеству допустимых начальных состояний автомата. Вершину 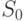 поместим на вертикальную прямую, называемую далее линией уровня, и присвоим ей номер 1. Определим далее подмножества
поместим на вертикальную прямую, называемую далее линией уровня, и присвоим ей номер 1. Определим далее подмножества 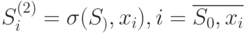 , и все полученные попарно различные подмножества, отличные от
, и все полученные попарно различные подмножества, отличные от 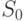 , также включим в число вершин графа. Ясно, что
, также включим в число вершин графа. Ясно, что  . Упорядочим множества
. Упорядочим множества 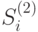 по мощности и будем располагать соответствующие им вершины графа на второй, третьей и т. д. линиях уровня по следующему принципу: на 2-ю линию уровня поместим все те вершины
по мощности и будем располагать соответствующие им вершины графа на второй, третьей и т. д. линиях уровня по следующему принципу: на 2-ю линию уровня поместим все те вершины  , у которых
, у которых 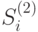 , на 3-ю линию - все те вершины, у которых
, на 3-ю линию - все те вершины, у которых  и т. д. Затем вершина
и т. д. Затем вершина 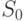 соединяется с каждой вершиной
соединяется с каждой вершиной 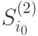 дугой с символом
дугой с символом 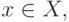 если
если  . В частности, если существует
. В частности, если существует  , такой, что
, такой, что 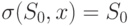 , то у вершины
, то у вершины 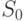 проводится петля с символом
проводится петля с символом  . Пусть
. Пусть 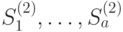 - все попарно различные вершины, появившиеся в графе на втором шаге. Определим теперь подмножества
- все попарно различные вершины, появившиеся в графе на втором шаге. Определим теперь подмножества  для всех
для всех  и для всех
и для всех  . Все полученные попарно различные подмножества, отличные от появившихся на втором шаге, также включим в число вершин графа. Затем упорядочиваем их по мощности, размещаем их на соответствующих линиях уровня, как это описано выше, и соединяем все вершины
. Все полученные попарно различные подмножества, отличные от появившихся на втором шаге, также включим в число вершин графа. Затем упорядочиваем их по мощности, размещаем их на соответствующих линиях уровня, как это описано выше, и соединяем все вершины 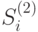 с вершинами
с вершинами 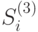 соответствующими дугами по ранее определенному правилу. В силу того что
соответствующими дугами по ранее определенному правилу. В силу того что  , все упомянутые дуги либо связывают между собой вершины, находящиеся на одной и той же линии уровня (в случае, когда
, все упомянутые дуги либо связывают между собой вершины, находящиеся на одной и той же линии уровня (в случае, когда  ), либо идут от вершин
), либо идут от вершин 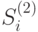 к вершинам
к вершинам 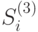 , находящимся на линиях уровня с большими номерами (в случае, когда
, находящимся на линиях уровня с большими номерами (в случае, когда  ).
).
Описанный процесс продолжается далее аналогичным образом до тех пор, пока на очередном шаге построения ГСА будут отсутствовать вершины, отличные от тех, что уже появились в графе на предшествующих шагах. Понятно, что построение ГСА обязательно завершится, поскольку число всевозможных подмножеств множества S состояний автомата конечно, причем число линий уровня ГСА не превосходит величины 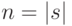 .
.
В полученном графе осуществим параллельный перенос всех линий уровня вправо так, чтобы 1-я из них оказалась между вершинами 1-го и 2-го уровней, 2-я - между вершинами 2-го и 3-го уровней и т. д. В результате такого переноса смещенные линии уровня будут пересекаться дугами, соединяющими между собой вершины  -го и
-го и  -го уровней
-го уровней 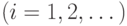 . Все упомянутые точки пересечения будем также считать вершинами графа промежуточными и каким-либо образом их перенумеруем. Именем каждой из появившихся промежуточных вершин будем считать присвоенный ей при упомянутой нумерации номер.
. Все упомянутые точки пересечения будем также считать вершинами графа промежуточными и каким-либо образом их перенумеруем. Именем каждой из появившихся промежуточных вершин будем считать присвоенный ей при упомянутой нумерации номер.
Удалим из этого графа все петли и поставим в соответствие каждой дуге графа число, трактуемое как длина дуги, равное весу помеченного ею входного символа. С каждой парой дуг графа  (здесь
(здесь 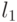 - номер некоторой промежуточной вершины), полученной из дуги
- номер некоторой промежуточной вершины), полученной из дуги 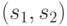 с пометкой
с пометкой 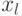 за счет переноса линий уровня, поступим следующим образом. Дугу
за счет переноса линий уровня, поступим следующим образом. Дугу 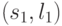 пометим пустым
пометим пустым  символом и поставим ей в соответствие число 0, а дуге
символом и поставим ей в соответствие число 0, а дуге 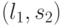 оставим пометку
оставим пометку  дуги
дуги 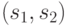 и поставим ей в соответствие число, равное весу символа
и поставим ей в соответствие число, равное весу символа 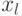 . Полученный в результате граф будем называть ГСА.
. Полученный в результате граф будем называть ГСА.
Из самого способа построения ГСА вытекает, что заданный автомат будет иметь СП тогда и только тогда, когда в соответствующем ему ГСА имеются вершины, помеченные символами одноэлементных подмножеств множества  состояний автомата. При этом последовательность входных символов, соответствующая пути по ГСА из вершины
состояний автомата. При этом последовательность входных символов, соответствующая пути по ГСА из вершины 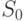 в одну из одноэлементных вершин, очевидно, будет являться СП.
в одну из одноэлементных вершин, очевидно, будет являться СП.
Для иллюстрации на рис.2.1 изображен граф синхронизации автомата, заданного табл. 1.1. Граф построен в предположении, что 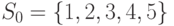 .
.
Далее покажем, что рассматриваемая нами задача синтеза СП может быть сведена к задаче выбора наискорейшего пути, решаемой методом динамического программирования [15] из теории оптимального управления. Последняя задача решается поэтапно с помощью процесса перемещения с одной опорной прямой на соседнюю. В нашем случае роль таких опорных прямых играют линии уровня, введенные нами при построении ГСА. Напомним, что из содержательного смысла задачи о выборе наискорейшего пути сетка дорог, ведущая из начального в конечный пункт, имеет некоторые особенности. Так, во-первых, в ней не должно быть петель, поскольку движение по ним не приближает нас к конечному пункту, а, во-вторых, все дуги, соответствующие участкам дорог от пунктов, расположенных на  -й опорной прямой, должны либо вести к пунктам на
-й опорной прямой, должны либо вести к пунктам на  -й опорной прямой, либо соединять между собой пункты на i-й опорной прямой, но не должно быть "обратных" дуг.
-й опорной прямой, либо соединять между собой пункты на i-й опорной прямой, но не должно быть "обратных" дуг.
Понятно, что если веса дуг в ГСА интерпретировать как время движения по ним, а сам ГСА как сеть дорог, то задача о синтезе СП минимального веса эквивалентна задаче о выборе наискорейшего пути из вершины 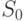 ГСА в одну из одноэлементных вершин того же графа. Действительно, ГСА удовлетворяет по построению всем требованиям, предъявляемым к сети дорог в упомянутой задаче. В качестве примера рассмотрим применение метода динамического программирования к построению минимальной по весу СП, переводящей автомат, заданный табл. 1.1, в конечное состояние 4, предполагая что
ГСА в одну из одноэлементных вершин того же графа. Действительно, ГСА удовлетворяет по построению всем требованиям, предъявляемым к сети дорог в упомянутой задаче. В качестве примера рассмотрим применение метода динамического программирования к построению минимальной по весу СП, переводящей автомат, заданный табл. 1.1, в конечное состояние 4, предполагая что 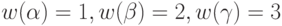 , а множество допустимых начальных состояний есть
, а множество допустимых начальных состояний есть 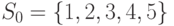 .
.
Вначале введем две дополнительные линии уровня: нулевую, на которой будет располагаться вершина 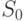 ГСА, и
ГСА, и  -ю, на которой будут располагаться вершины ГСА, лежащие правее линии уровня с номером
-ю, на которой будут располагаться вершины ГСА, лежащие правее линии уровня с номером 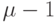 , где
, где 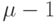 есть максимальный номер уровня, появившийся в процессе построения ГСА, описанном выше. В рассматриваемом примере максимальный номер уровня, появившийся при построении ГСА на рис.2.1, равен 4, поэтому на 5-й линии уровня будут расположены все одноэлементные вершины
есть максимальный номер уровня, появившийся в процессе построения ГСА, описанном выше. В рассматриваемом примере максимальный номер уровня, появившийся при построении ГСА на рис.2.1, равен 4, поэтому на 5-й линии уровня будут расположены все одноэлементные вершины  , а на нулевом - вершина
, а на нулевом - вершина 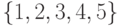 .
.
Напомним, что в методе динамического программирования каждый шаг представляет собой перемещение с одной из опорных прямых (линии уровня) на соседнюю, более близкую к конечному пункту (в нашем примере к вершине 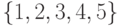 ). При этом, как обычно, предполагается, что движение от шага к шагу допускается только в положительном направлении (от вершины
). При этом, как обычно, предполагается, что движение от шага к шагу допускается только в положительном направлении (от вершины 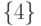 к вершине
к вершине 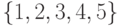 ). Иными словами, после того как некоторый шаг пройден, возвращение обратно, в ту же полосу между двумя линиями уровня, не допускается.
). Иными словами, после того как некоторый шаг пройден, возвращение обратно, в ту же полосу между двумя линиями уровня, не допускается.
В соответствии с числом линий уровня на рис.2.1 процесс перемещения из вершины 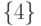 в вершину
в вершину 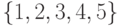 разделим на пять шагов и начнем построение оптимального пути с последнего пятого шага.
разделим на пять шагов и начнем построение оптимального пути с последнего пятого шага.
Наметим на четвертой линии уровня все возможные пункты (вершины) нашего движения в момент окончания предпоследнего четвертого шага. В нашем примере такими вершинами будут вершины 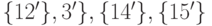 . Далее находим оптимальные по времени пути из этих вершин в вершину
. Далее находим оптимальные по времени пути из этих вершин в вершину 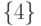 . Заметим, что для поиска таких путей можно применить, например, известные алгоритмы Флойда и Данцига поиска всех кратчайших путей в ориентированном графе [34].
. Заметим, что для поиска таких путей можно применить, например, известные алгоритмы Флойда и Данцига поиска всех кратчайших путей в ориентированном графе [34].
После завершения этого шага переходим к планированию четвертого шага. Для каждой из вершин 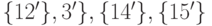 теперь необходимо найти оптимальное управление, т. е. такой путь с 3-й линии уровня на 4-ю, который совместно с уже оптимизированным последним шагом дает возможность достигнуть вершины
теперь необходимо найти оптимальное управление, т. е. такой путь с 3-й линии уровня на 4-ю, который совместно с уже оптимизированным последним шагом дает возможность достигнуть вершины 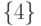 за минимальное время.
за минимальное время.
Чтобы найти это условное оптимальное управление, для каждой вершины на 3-й линии уровня необходимо перебрать всевозможные способы перехода на 4-ю линию уровня и время, которое требуется на этот переход, сложить с минимальным временем последнего шага. Из всех возможных путей выбирается тот, для которого это суммарное время минимально, и соответствующий путь отмечается. Понятно, что и на этом шаге для поиска кратчайших путей между соответствующими вершинами ГСА 3-й и 4-й линий уровня можно применить алгоритмы Флойда и Данцига.
В результате цепочки таких построений, перемещаясь шаг за шагом с одной линии уровня на другую, дойдем до исходной вершины 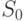 . Для нее определим оптимальный путь на первую линию уровня. Таким образом, теперь мы располагаем всеми данными для построения оптимального пути, так как для каждой из намеченных вершин на линиях уровня известно оптимальное продолжение пути. Для нашего примера в результате завершения процесса будет найден оптимальный путь
. Для нее определим оптимальный путь на первую линию уровня. Таким образом, теперь мы располагаем всеми данными для построения оптимального пути, так как для каждой из намеченных вершин на линиях уровня известно оптимальное продолжение пути. Для нашего примера в результате завершения процесса будет найден оптимальный путь

Ему соответствует последовательность входных сигналов 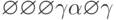 . Если исключить из нее пустые сигналы, то получится искомая минимальная по весу СП
. Если исключить из нее пустые сигналы, то получится искомая минимальная по весу СП 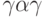 , переводящая заданный автомат из любого состояния в одно и то же конечное состояние 4.
, переводящая заданный автомат из любого состояния в одно и то же конечное состояние 4.
Выбирая далее в качестве конечной вершины пути все остальные одноэлементные вершины ГСА, находящиеся на 5-й линии уровня, найдем описанным выше образом минимальные по весу СП, переводящие автомат в эти конечные состояния. Заметим, что в общем случае не все такие пути могут существовать, что говорит о невозможности перевода автомата в соответствующее конечное состояние, если он стартует из любого состояния множества 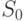 . Наконец, выбрав из всех построенных условно оптимальных по весу СП минимальную, получим искомую СП. Легко убедиться, что в нашем примере такой минимальной по весу СП будет
. Наконец, выбрав из всех построенных условно оптимальных по весу СП минимальную, получим искомую СП. Легко убедиться, что в нашем примере такой минимальной по весу СП будет 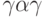 , построенная выше.
, построенная выше.

