|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Принятие решений на основе моделей обеспечения качества
Основы теории статистического контроля
Выборочный контроль, построенный на научной основе, т.е. исходящий из теории вероятностей и математической статистики, называют статистическим контролем. Предпринимателя и менеджера выборочный контроль может интересовать не только в связи с качеством продукции, но и в связи, например, с контролем экологической обстановки, поскольку зафиксированные государственными органами экологические нарушения влекут штрафы и иные "неприятные" последствия. Или в связи с выборочным контролем документации.
Обсудим основные подходы статистического контроля.
При статистическом контроле решение о генеральной совокупности - об экологической обстановке в данном регионе или о партии продукции - принимается по выборке, состоящей из некоторого количества единиц (единиц экологического контроля или единиц продукции). Следовательно, выборка должна представлять партию, т.е. быть репрезентативной (представительной). Как эти слова понимать, как проверить репрезентативность? Ответ может быть дан лишь в терминах вероятностных моделей выборки.
Наиболее распространенными являются две вероятностные модели - биномиальная и гипергеометрическая. В первой из них предполагается, что результаты контроля  единиц можно рассматривать как совокупность n независимых одинаково распределенных случайных величин
единиц можно рассматривать как совокупность n независимых одинаково распределенных случайных величин 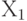 ,
, 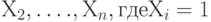 , если
, если  ое измерение показывает, что имеется нарушение, т.е. превышено ПДК (предельная норма концентрации) или
ое измерение показывает, что имеется нарушение, т.е. превышено ПДК (предельная норма концентрации) или  ое изделие дефектно, и
ое изделие дефектно, и  , если это не так. Тогда число
, если это не так. Тогда число  превышений ПДК (при другой интерпретации - дефектных единиц продукции в партии) равно
превышений ПДК (при другой интерпретации - дефектных единиц продукции в партии) равно
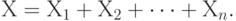 |
( 1) |
Известно, что распределение  имеет вид
имеет вид
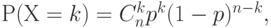 |
( 2) |
где 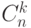 - число сочетаний из
- число сочетаний из  элементов по
элементов по  , а
, а  -уровень дефектности (в другой предметной области - в экологии - доля превышений ПДК в генеральной совокупности), т.е.
-уровень дефектности (в другой предметной области - в экологии - доля превышений ПДК в генеральной совокупности), т.е. 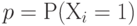 . Формула (2) задает так называемое биномиальное распределение.
. Формула (2) задает так называемое биномиальное распределение.
Из формулы (1) и Центральной Предельной Теоремы теории вероятностей вытекает, что при увеличении объема выборки n распределение  сближается с нормальным распределением.
сближается с нормальным распределением.
Вторая модель - гипергеометрическая - соответствует случайному отбору единиц в выборку. Пусть среди  единиц, составляющих генеральную совокупность, имеется
единиц, составляющих генеральную совокупность, имеется  дефектных. Случайность отбора означает, что каждая единица имеет одинаковые шансы попасть в выборку. Более того, ни одна пара единиц не имеет преимущества перед любой другой парой при отборе в выборку. То же самое - для троек, четверок и т.д. Итак, каждое из сочетаний по
дефектных. Случайность отбора означает, что каждая единица имеет одинаковые шансы попасть в выборку. Более того, ни одна пара единиц не имеет преимущества перед любой другой парой при отборе в выборку. То же самое - для троек, четверок и т.д. Итак, каждое из сочетаний по  единиц из
единиц из  имеет одинаковую вероятность быть отобранным в качестве выборки, равную, очевидно,
имеет одинаковую вероятность быть отобранным в качестве выборки, равную, очевидно,  .
.
Отбор случайной выборки согласно описанным правилам организуют при проведении различных лотерей. Пусть  -число дефектных единиц в такой выборке. Известно, что тогда
-число дефектных единиц в такой выборке. Известно, что тогда 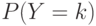 - гипергеометрическое распределение, т.е.
- гипергеометрическое распределение, т.е.
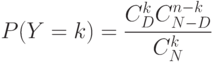
Замечательный математический результат состоит в том, что биномиальная и гипергеометрическая модели весьма близки, когда объем генеральной совокупности (партии) по крайней мере в 10 раз превышает объем выборки. Таким образом, можно констатировать, что
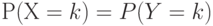 |
( 3) |
с достаточной для практики точностью, если объем выборки мал по сравнению с объемом партии. При этом в качестве p в формуле (2) берут 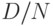 .
.
Близость результатов, получаемых с помощью биномиальной и гипергеометрической моделей, весьма важна с методологической точки зрения. Дело в том, что эти модели исходят из принципиально различных методологических предпосылок. В биномиальной модели случайность присуща каждой единице - она с какой-то вероятностью дефектна, а с какой-то - годна. В то же время в гипергеометрической модели качество определенной единицы детерминировано, задано, а случайность проявляется лишь в отборе, вносится инженером, экологом или экономистом при составлении выборки.
В науках о человеке противоречие между двумя рассматриваемыми моделями выборки еще более выражено. Биномиальная модель предполагает, что поведение человека, в частности, выбор им определенного варианта при ответе на вопрос, определяется с участием случайных причин. Например, человек может случайно сказать "да", случайно - "нет". Некоторые философы отрицают присущую поведению человека случайность. Они верят в причинность и считают поведение конкретного человека практически полностью определенным (детерминированным) его взглядами, жизненным опытом, окружающей средой. Поэтому они принимают гипергеометрическую модель и считают, что случайность отличия ответов в выборке от ответов во всей генеральной совокупности определяется всецело случайностью, вносимой при отборе единиц наблюдения в выборку.
Соотношение (3) показывают, что во многих случаях нет необходимости выбирать одну из моделей, поскольку обе дают близкие численные результаты. Отличия проявляются при обсуждении вопроса о том, какую выборку считать представительной. Является ли таковой выборка, составленная из 20 изделий, лежащих сверху в первом вскрытом ящике? В биномиальной модели вполне допустим ответ "да", в гипергеометрической - только "нет".
Биномиальная модель легче для теоретического изучения, поэтому будем её рассматривать в дальнейшем. Однако при реальном контроле лучше формировать выборку, исходя из гипергеометрической модели. Это делают, выбирая номера изделий (для включения в выборку) с помощью датчиков псевдослучайных чисел на ЭВМ или с помощью таблиц псевдослучайных чисел. Алгоритмы формирования выборки встраивают в современные программные продукты по статистическому контролю.
Планы статистического контроля и правила принятия решений. Под планом статистического контроля понимают алгоритм, т.е. правила действий при контроле качества. На "входе" при этом - генеральная совокупность (партия продукции), а на "выходе" - одно из двух решений: "принять партию" либо "забраковать партию". Рассмотрим несколько примеров.
Одноступенчатые планы контроля 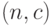 : отобрать выборку объема n; если число дефектных единиц в выборке
: отобрать выборку объема n; если число дефектных единиц в выборке  не превосходит
не превосходит  , то партию принять, в противном случае забраковать. Число с называется "приемочным числом".
, то партию принять, в противном случае забраковать. Число с называется "приемочным числом".
Частные случаи: план 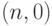 -партию принять тогда и только тогда, когда все единицы в выборке являются годными; план
-партию принять тогда и только тогда, когда все единицы в выборке являются годными; план 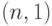 - партия принимается, если в выборке все единицы являются годными или ровно одно - дефектное, во всех остальных случаях партия бракуется.
- партия принимается, если в выборке все единицы являются годными или ровно одно - дефектное, во всех остальных случаях партия бракуется.
Двухступенчатый план контроля 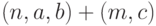 : отобрать первую выборку объема n; если число дефектных единиц в первой выборке
: отобрать первую выборку объема n; если число дефектных единиц в первой выборке  не превосходит
не превосходит  , то партию принять; если число дефектных единиц в первой выборке
, то партию принять; если число дефектных единиц в первой выборке  больше или равно
больше или равно  , то партию забраковать; во всех остальных случаях, т.е. когда
, то партию забраковать; во всех остальных случаях, т.е. когда  больше
больше  , но меньше
, но меньше  , следует взять вторую выборку объема
, следует взять вторую выборку объема  ; если число дефектных единиц во второй выборке
; если число дефектных единиц во второй выборке  не превосходит
не превосходит  , то партию принять, в противном случае забраковать.
, то партию принять, в противном случае забраковать.
Рассмотрим в качестве примера план 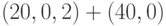 . Сначала берется первая выборка объема 20. Если все единицы в ней - годные, то партия принимается. Если две или больше - дефектные, партия бракуется. А если только одно - дефектное? В реальной ситуации в таких случаях начинаются споры между представителями предприятия и экологического контроля, или поставщика и потребителя. Говорят, например, что дефектная единица случайно попала в партию, что ее подсунули конкуренты или что при контроле случайно сделан неправильный вывод. Поэтому, чтобы споры пресечь, берут вторую выборку объема 40 (вдвое большего, чем в первый раз). Если все единицы во второй выборке - годные, то партию принимают, в противном случае - бракуют.
. Сначала берется первая выборка объема 20. Если все единицы в ней - годные, то партия принимается. Если две или больше - дефектные, партия бракуется. А если только одно - дефектное? В реальной ситуации в таких случаях начинаются споры между представителями предприятия и экологического контроля, или поставщика и потребителя. Говорят, например, что дефектная единица случайно попала в партию, что ее подсунули конкуренты или что при контроле случайно сделан неправильный вывод. Поэтому, чтобы споры пресечь, берут вторую выборку объема 40 (вдвое большего, чем в первый раз). Если все единицы во второй выборке - годные, то партию принимают, в противном случае - бракуют.
В реальной нормативно-технической документации - договорах на поставку, технических регламентах, стандартах, технических условиях, инструкциях по экологическому контролю и т.д. - не всегда четко сформулированы планы статистического контроля и правила принятия решений. Например, при описании двухступенчатого плана контроля вместо задания приемочного числа с может стоять загадочная фраза "результат контроля второй выборки считается окончательным". Остается гадать, как принимать решение по второй выборке. Менеджер, администратор (государственный служащий), инженер, эколог или экономист, занимающийся вопросами экологического контроля или контроля качества, должен первым делом добиваться кристальной ясности в формулировках правил принятия решений, иначе ошибочные и необоснованные решения, а потому и убытки неизбежны.
Оперативная характеристика плана статистического контроля. Каковы свойства плана статистического контроля? Они, как правило, определяются с помощью функции 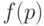 , связывающей вероятность
, связывающей вероятность  дефектности единицы контроля с вероятностью
дефектности единицы контроля с вероятностью 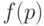 приемки партии, положительной оценки экологической обстановки или заключения о правильности ведения бухгалтерской документации по результатам контроля. При этом вероятность p того, что конкретная единица дефектна, называется входным уровнем дефектности, а указанная функция называется оперативной характеристикой плана контроля. Если дефектные единицы отсутствуют,
приемки партии, положительной оценки экологической обстановки или заключения о правильности ведения бухгалтерской документации по результатам контроля. При этом вероятность p того, что конкретная единица дефектна, называется входным уровнем дефектности, а указанная функция называется оперативной характеристикой плана контроля. Если дефектные единицы отсутствуют,  , то партия всегда принимается, т.е.
, то партия всегда принимается, т.е.  . Если все единицы дефектные,
. Если все единицы дефектные,  , то партия наверняка бракуется,
, то партия наверняка бракуется, 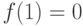 . Между этими крайними значениями
. Между этими крайними значениями 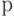 функция
функция 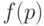 монотонно убывает. При изучении свойств плана входной уровень дефектности
монотонно убывает. При изучении свойств плана входной уровень дефектности 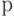 - свободный параметр, он
может принимать любые значения между 0 и 1.
- свободный параметр, он
может принимать любые значения между 0 и 1.
Вычислим оперативную характеристику плана 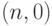 . Поскольку партия принимается тогда и только тогда, когда все единицы являются годными, а вероятность того, что конкретная единица - годная, равна
. Поскольку партия принимается тогда и только тогда, когда все единицы являются годными, а вероятность того, что конкретная единица - годная, равна 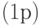 , то оперативная характеристика имеет вид
, то оперативная характеристика имеет вид
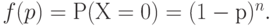 |
( 4) |
Для плана 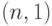 оперативная характеристика, как легко видеть, такова:
оперативная характеристика, как легко видеть, такова:
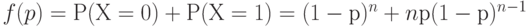 |
( 5) |
Оперативные характеристики для конкретных планов статистического контроля не всегда имеют такой простой вид, как в случае формул (4) и (5). Рассмотрим в качестве примера план (20, 0, 2) + (40, 0). Сначала найдем вероятность того, что партия будет принята по результатам контроля первой партии. Согласно формуле (4) имеем:

Вероятность того, что понадобится контроль второй выборки, равна

При этом вероятность того, что по результатам её контроля партия будет принята, равна
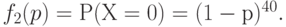
Следовательно, вероятность того, что партия будет принята со второй попытки, т.е. что при контроле первой выборки обнаружится ровно одна дефектная единица, а затем при контроле второй - ни одной, равна
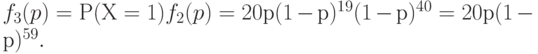
Следовательно, вероятность принятия партии с первой или со второй попытки равна
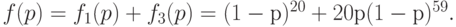
При практическом применении методов статистического приемочного контроля для нахождения оперативных характеристик планов контроля вместо формул, имеющих обозримый вид лишь для отдельных видов планов, применяют численные компьютерные алгоритмы или заранее составленные таблицы.
