Использование формального аппарата для оптимизации схем отношений
8.3. Декомпозиция схемы отношения
Последовательный переход от одной нормальной формы к другой при нормализации схем отношений реализуется через декомпозицию. Основной операцией, с помощью которой осуществляется декомпозиция, является проекция.
Декомпозицией схемы отношения R = {А1, А2, ...,Аn} называется замена ее совокупностью подмножеств R, таких, что их объединение дает R. При этом допускается, чтобы подмножества были пересекающимися.
Алгоритм декомпозиции основан на следующей теореме.
Теорема о декомпозиции. Пусть R(A, B, C) – отношение, A, B, C – атрибуты.
Если R удовлетворяет зависимости A->B, то R равно соединению его проекций A, B и A, C
R(A, B, C) = R(A, B), R(A, C)
При нормализации необходимо выбирать такие декомпозиции, которые обладают свойством соединения без потерь. В этом случае, декомпозиция должна обеспечить то, что запросы (выборка данных по условию) к исходному отношению и отношениям, получаемым в результате декомпозиции, дадут одинаковый результат. Соответствующее условие будет выполняться, если каждый кортеж отношения R может быть представлен как естественное соединение его проекций на каждое из подмножеств. Для проверки, обладает ли декомпозиция данным свойством, используется специальные алгоритмы, описанные в литературе (в данной книге не рассматриваются).
Вторым важнейшим желательным свойством декомпозиции является свойство сохранения функциональных зависимостей. Стремление к тому, чтобы декомпозиция сохраняла зависимости, естественно. Функциональные зависимости являются некоторыми ограничениями на данные. Если декомпозиция не обладает этим свойством, то для того чтобы проверить, не нарушаются ли при вводе данных условия целостности (функциональные зависимости), нам приходится соединять все проекции.
Таким образом, для правильно построенного проекта базы данных необходимо, чтобы декомпозиции обладали свойством соединения без потерь, и желательно, чтобы они обладали свойством сохранения функциональных зависимостей.
8.4 .Выбор рационального набора схем отношений путем нормализации
Вторая нормальная форма (2НФ)
Отношение находится в 2НФ, если оно находится в 1НФ и каждый неключевой атрибут зависит от всего первичного ключа (не зависит от части ключа).
Для перевода отношения в 2НФ необходимо, используя операцию проекции, разложить его на несколько отношений следующим образом:
- построить проекцию без атрибутов, находящихся в частичной функциональной зависимости от первичного ключа;
- построить проекции на части составного ключа и атрибуты, зависящие от этих частей.
Третья нормальная форма (3НФ)
Отношение находится в 3НФ, если оно находится в 2НФ и каждый ключевой атрибут нетранзитивно зависит от первичного ключа.
Отношение находится в 3НФ в том и только том случае, если все неключевые атрибуты отношения взаимно независимы и полностью зависят от первичного ключа.
Оказывается, что любая схема отношений может быть приведена к 3НФ декомпозицией, обладающей свойствами соединения без потерь и сохраняющей зависимости.
Мотивировка третьей нормальной формы
Третья нормальная форма исключает избыточность и аномалии включения и удаления.
К сожалению, 3НФ не предотвращает все возможные аномалии.
Нормальная форма Бойса-Кодда (НФБК)
Если в R для каждой зависимости X->A, где А не принадлежит X, X включает в себя некоторый ключ, то говорят, что данное отношение находится в нормальной форме Бойса-Кодда.
Детерминантом функциональной зависимости называется минимальная группа атрибутов, от которой зависит некоторый другой атрибут или группа атрибутов, причем эта зависимость нетривиальная.
Отношение находится в НФБК тогда и только тогда, когда каждый его детерминант является потенциальным ключом.
НФБК является более строгой версией 3НФ. Иными словами, любое отношение, находящееся в НФБК, находится в 3НФ. Обратное неверно.
Мотивировка нормальной формы Бойса-Кодда
В нормальной форме Бойса-Кодда не существует избыточности и аномалий включения, удаления и модификации. Оказывается, что любая схема отношения может быть приведена в нормальную форму Бойса-Кодда таким образом, чтобы декомпозиция обладала свойством соединения без потерь. Однако схема отношения может быть неприводимой в НФБК с сохранением зависимостей. В этом случае приходится довольствоваться третьей нормальной формой.
8.5. Пример нормализации до 3НФ
Для улучшения структуры реляционной базы данных (устранения возможных аномалий) необходимо привести все таблицы базы данных к третьей нормальной форме или в более высокой форме (если это возможно). Таким образом, задача сводится к проверке нормализации всех сущностей, отображающихся в таблицы базы данных. Если таблица, получающаяся из некоторой сущности, не является таблицей в третьей нормальной форме, то она должна быть заменена на несколько таблиц, находящихся в третьей нормальной форме.
Продолжим рассмотрение примера с отношением ЭКЗАМЕНАЦИОННАЯ ВЕДОМОСТЬ
В начале этой лекции мы привели отношение к первой нормальной форме.
| Код студента | Фамилия | Код экзамена | Предмет | Дата | Оценка |
|---|---|---|---|---|---|
| 1 | Сергеев | 1 | Математика | 5.08.03 | 4 |
| 2 | Иванов | 1 | Математика | 5.08.03 | 5 |
| 1 | Сергеев | 2 | Физика | 9.08.03 | 5 |
| 2 | Иванов | 2 | Физика | 9.08.03 | 5 |
Ключом данного отношения будет совокупность атрибутов – Код студента и Код экзамена.
Для более краткой записи процесса нормализации введем следующие обозначения:
КС – код студента, КЭ – код экзамена, Ф – фамилия, П – предмет, Д – дата, О - оценка.
Выпишем функциональные зависимости
КС, КЭ -> Ф, П, Д, О КС, КЭ -> Ф КС, КЭ -> П КС, КЭ -> Д КС, КЭ -> О КЭ -> П КЭ -> Д КС -> Ф
В соответствии с определением, отношение находится во второй нормальной форме (2НФ), если оно находясь в 1НФ и каждый неключевой атрибут зависит от первичного ключа и не зависит от части ключа. Здесь атрибуты П, Д, Ф зависят от части ключа. Чтобы избавиться от этих зависимостей необходимо произвести декомпозицию отношения. Для этого используем теорему о декомпозиции.
Имеем отношение R(КС, Ф, КЭ, П, Д, О). Возьмем зависимость КС -> Ф в соответствии с формулировкой теоремы исходное отношение равно соединению его проекций R1(КС, Ф) и R2(КС, КЭ, П, Д, О).
В отношении R1(КС, Ф) существует функциональная зависимость КС -> Ф, ключ КС – составной, не ключевой атрибут Ф не зависит от части ключа. Это отношение находится в 2НФ. Так как в этом отношении нет транзитивных зависимостей, отношение R(КС, Ф) находится в 3НФ, что и требовалось.
Рассмотрим отношение R2(КС, КЭ, П, Д, О) с составным ключом КС, КЭ. Здесь есть зависимость КЭ -> П, КЭ -> Д, КЭ -> П, Д. Атрибуты П,Д зависят от части ключа, следовательно отношение не находится в 2НФ. В соответствии с теоремой о декомпозиции исходное отношение (используем функциональную зависимость КЭ -> П, Д) равно соединению проекций R3(КЭ, П, Д), R4(КС, КЭ, О). В отношении R3( КЭ, П, Д) существуют функциональные зависимости КЭ -> П, КЭ -> Д, КЭ -> П, Д. Зависимости неключевых атрибутов от части ключа нет, следовательно отношение находится в 2НФ. Транзитивных зависимостей в этом отношении так же нет, следовательно отношение находится в 3НФ.
Таким образом, исходное отношение приведено в к трем отношениям, каждое из которых находится в третьей нормальной форме R1(КС, Ф), R3(КЭ, П, Д), R4(КС, КЭ, О).
Заметим, что в отношении R4 атрибуты КС, КЭ являются внешними ключами, используемыми для установления связей с другими отношениями. Представим полученную модель в виде диаграммы объектов-связей (ER-диаграммы). Для наглядности и возможности последующего программирования перейдем к английским названиям объектов (отношений) и атрибутов.
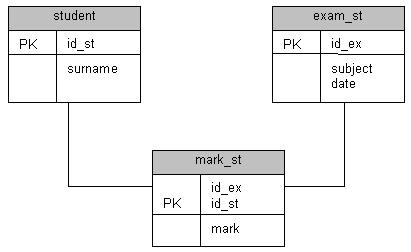
Отношение R1 представляет объект student с атрибутами id_st (первичный ключ), surname.
Отношение R3 представляет объект exam_st c атрибутами id_ex (первичный ключ), subject, date.
Отношение R4 представляет объект mark_st c атрибутами id_st (внешний ключ), id_ex (внешний ключ), mark. Первичный ключ здесь id_st, id_ex.
Соответствующая ER-диаграмма изображена на рис. 8.1.