Использование формального аппарата для оптимизации схем отношений
Цель лекции: показать возможность эффективного использования формальных методов построения оптимальной (по определенным показателям) структуры реляционной базы данных путем нормализации схем отношений.
8.1. Проблема выбора рациональных схем отношений
При представлении концептуальной схемы в виде реляционной модели возможны различные варианты выбора схем отношений. Одни варианты выбора рассматривались в предыдущих разделах (п. 6.2.3), другие получаются объединением (или разбиением) некоторых схем отношений. От правильного выбора схем отношений, представляющих концептуальную схему, в значительной степени будет зависеть эффективность функционирования базы данных.
Рассмотрим для примера конкретную схему отношений и проанализируем её недостатки. Предположим, что данные о студентах, факультетах, специальностях, включены в таблицу со следующей схемой отношения: СТУДЕНТ (Код студента, Фамилия, Название факультета, Название специальности).
Эта схема отношений обусловливает следующие недостатки соответствующей базы данных:
- Дублирование информации (избыточность). У студентов, обучающихся на одном факультете, будет повторяться название факультета. Для разных факультетов будут повторяться специальности.
- Потенциальная противоречивость ( аномалии обновления ). Если, например, изменится название специальности, то изменяя её в одном кортеже (у одного студента), необходимо изменять и во всех других кортежах, где она присутствует.
- Потенциальная возможность потери сведений ( аномалии удаления ). При удалении информации о всех студентах, поступающих на определенную специальность, мы теряем все сведения об этой специальности.
- Потенциальная возможность невключения информации в базу данных ( аномалии включения ). В базе данных будут отсутствовать сведения о специальности, если на ней нет обучающихся студентов.
В теории реляционных баз данных существуют формальные методы построения реляционной модели базы данных, в которой отсутствует избыточность и аномалии обновления, удаления и включения.
Нормализация. Первая нормальная форма.
Построение рационального варианта схем отношений (обладающего лучшими свойствами при операциях включения, модификации и удаления данных, чем все остальные наборы схем) осуществляется путем так называемой нормализации схем отношений. Нормализация производится в несколько этапов. На начальном этапе схема отношений должна находиться в первой нормальной форме (1НФ).
Отношение находится в первой нормальной форме, если все атрибуты отношения принимают простые значения (атомарные или неделимые), не являющиеся множеством или кортежем из более элементарных составляющих.
Рассмотрим следующий пример.
Таблица представляет сущность ЭКЗАМЕНАЦИОННАЯ ВЕДОМОСТЬ
| Код студента | Фамилия | Код экзамена | Предмет и дата | Оценка |
|---|---|---|---|---|
| 1 | Сергеев | 1 | Математика 5.06.08 | 4 |
| 2 | Иванов | 1 | Математика 5.06.08 | 5 |
| 1 | Сергеев | 2 | Физика 9.06.08 | 5 |
| 2 | Иванов | 2 | Физика 9.06.08 | 5 |
Теперь на пересечении любой строки и любого столбца находится одно значение и, следовательно, данная таблица находится в первой нормальной форме.
Далее отношение, представленное в первой нормальной форме, последовательно преобразуется во вторую и третью нормальные формы. Процесс построения второй и третьей нормальных форм будет описан в следующих подразделах. При некоторых предположениях о данных третья нормальная форма является искомым наилучшим вариантом.
Если эти предположения не выполняются, то процесс нормализации продолжается и отношение преобразуется в четвертую и пятую нормальные формы. Построение соответствующих форм описано в литературе и в данной книге не рассматривается.
Прежде чем перейти к построению второй нормальной формы, необходимо определить ряд формальных понятий.
8.2. Функциональные зависимости (зависимости между атрибутами отношения)
Пусть R(A1, A2, ..., An) – схема отношения, а X и Y – подмножества {A1, A2, ..., An}.
Функциональная зависимость на отношении R – это утверждение вида "Если два кортежа R совпадают по атрибутам множества  (т.е. эти кортежи имеют в соответствующих друг другу компонентах одни и те же значения для каждого атрибута множества X ), то они должны совпадать и по атрибутам множества
(т.е. эти кортежи имеют в соответствующих друг другу компонентах одни и те же значения для каждого атрибута множества X ), то они должны совпадать и по атрибутам множества 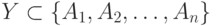 . Формально эта зависимость записывается выражением X -> Y, причем говорится, что X функционально определяет Y.
Часто используется другое утверждение: X функционально определяет Y или Y функционально зависит от X ( обозначается X -> Y ) тогда и только тогда, когда каждое значение множества X отношения R связано с одним значением множества Y отношения R. Иначе говоря, если два кортежа R совпадают по значению X, они совпадают и по значению Y.
. Формально эта зависимость записывается выражением X -> Y, причем говорится, что X функционально определяет Y.
Часто используется другое утверждение: X функционально определяет Y или Y функционально зависит от X ( обозначается X -> Y ) тогда и только тогда, когда каждое значение множества X отношения R связано с одним значением множества Y отношения R. Иначе говоря, если два кортежа R совпадают по значению X, они совпадают и по значению Y.
Замечание. Вообще говоря, под термином "отношение" могут подразумеваться два понятия:
- отношение как переменная, которая может принимать разные значения (таблица, в строки и столбцы которой могут быть вписаны разные значения);
- отношение, как набор конкретных значений (таблица с заполненными элементами).
Функциональные зависимости характеризуют все отношения, которые могут быть значениями схемы отношения R в принципе. Поэтому единственный способ определить функциональные зависимости – внимательно проанализировать семантику (смысл) атрибутов.
Функциональные зависимости являются, в частности, ограничениями целостности, поэтому целесообразно проверять их при каждом обновлении базы данных.
Пример функциональных зависимостей для отношения ЭКЗАМЕНАЦИОННАЯ ВЕДОМОСТЬ
Код студента -> Фамилия Код студента, Код экзамена -> Оценка
Пример функциональных зависимостей для отношения СТУДЕНТ, приведенного в начале настоящей лекции
Код студента -> Фамилия, Код студента -> Факультет
Заметим, что последняя зависимость существует при условии, что один студент не может обучаться на нескольких факультетах.
Полное множество функциональных зависимостей
Для каждого отношения существует вполне определенное множество функциональных зависимостей между атрибутами данного отношения. Причем из одной или более функциональных зависимостей, присущих рассматриваемому отношению, можно вывести другие функциональные зависимости, также присущие этому отношению.
Заданное множество функциональных зависимостей для отношения R обозначим F, полное множество функциональных зависимостей, которые логически можно получить из F, называется замыканием F и обозначается F+.
Если множество функциональных зависимостей совпадает с замыканием данного множества, то такое множество функциональных зависимостей называется полным.
Введенные понятия позволяют формально определить понятие ключа.
Пусть существует некоторая схема R с атрибутами A1A2...An, F – некоторое множество функциональных зависимостей и X – некоторое подмножество R. Тогда X называется ключом, если, во-первых, в F+ существует зависимость X -> A1A2...An и, во-вторых, ни для какого подмножества Y, входящего в X, зависимость Y -> A1A2...An не принадлежит F+.
Полной функциональной зависимостью называется зависимость неключевого атрибута от всего составного ключа.
Частичной функциональной зависимостью будем называть зависимость неключевого атрибута от части составного ключа.
Для вычисления замыкания множества функциональных зависимостей используются следующие правила вывода ( аксиомы Армстронга ):
Пусть известна некоторая схема отношения R{A1, A2, ..., An} с множеством атрибутов U={A1, A2, ..., An} и множество функциональных зависимостей F, заданных на множестве U.
Аксиома рефлексивности. Если Y входит в X, а X входит в 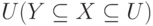 , то X->Y логически следует из F. Это правило дает тривиальные зависимости, так как в них правая часть содержится в левой части.
, то X->Y логически следует из F. Это правило дает тривиальные зависимости, так как в них правая часть содержится в левой части.
Аксиома пополнения. Если X->Y и Z есть подмножество U, то XZ->YZ. В данном случае функциональная зависимость X->Y либо содержалась в исходном множестве F, либо может быть выведена из F с использованием описываемых аксиом.
Аксиома транзитивности. Если X->Y и Y->Z, то X->Z.
Справедлива следующая теорема. Аксиомы Армстронга являются полными и надежными.
Это значит, что используя их мы выведем все возможные функциональные зависимости, логически следующие из F, и не выведем никаких лишних зависимостей.
Существует несколько других правил вывода, которые следуют из аксиом Армстронга.
Правило самоопределения. X->Х.
Правило объединения. Если X->Y и X->Z, то 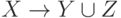 .
.
Правило псевдотранзитивности. Если X->Y и 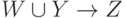 , то
, то 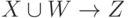 .
.
Правило композиции. Если X->Y и Z->W, то  .
.
Правило декомпозиции. Если X->Y и Z входит в Y, то X->Z.
Надо отметить, что вычисление замыкания множества функциональных зависимостей является трудоемкой задачей при достаточно большом количестве атрибутов (за счет выписывания большого количества тривиальных зависимостей).
