Процедурное программирование

11.2. Повторения и циклы

11.2.1. Оператор Do

Для описания оператора Do воспользуемся подходом Е. М. Воробьёва [1, с. 164–167].

Одним из основных операторов процедурного (равно как функционального и основанного на правилах преобразований) программирования является оператор присваивания Set. Преимуществом Mathematica перед другими языками программирования является то, что нет необходимости заранее определять тип выражения, которому осуществляется присваивание. Одному и тому же символу можно присвоить как символьные, так и численные значения, как комплексные, так и действительные величины.

Если в пределах одной ячейки мы несколько раз подряд осуществим операцию присваивания, разделяя следующие друг за другом выражения знаком " ; ", то записанные выражения в совокупности также будут являть собой некоторое выражение, которое называется составным выражением и имеет заголовок CompoundExpression.

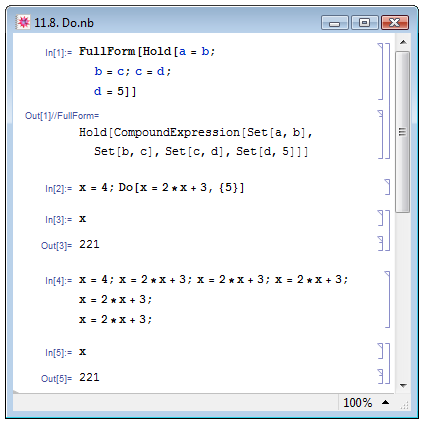
В примере In[1] на рис. 11.8 при помощи функции FullForm мы вывели на экран внутреннюю форму некоторого составного выражения a=b;b=c;c=d;d=5, при этом мы воспользовались функцией Hold для того, чтобы функция FullForm применялась непосредственно к заданному выражению, а не к результату его вычисления. Как мы видим в Out[1], дано выражение действительно имеет заголовок CompoundExpression.

Е. М. Воробьёв в [1, с. 165] отмечает следующее: "Оператором, в известном смысле имитирующим CompoundExpression, является оператор Do". По большому счёту, оператор Do организует цикл. Цикл — это разновидность управляющей конструкции в языках программирования высокого уровня, предназначенная для организации многократного исполнения набора инструкций.

Выражение Do[expr,{imax}], заданное в простейшей форме, imax раз вычисляет выражение expr. Очевидно, что это выражение полностью эквивалентно выражению expr;expr;...;expr;, при этом стоит отметить, что последнее выражение в данном составном выражении также завершается знаком " ; ". Таким образом, после вычисления выражения Do[expr,{imax}] ячейка Out не генерируется.

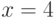В примерах In[2] и In[4] на рис. 11.8 мы пять раз вычислили выражение , задав перед вычислением значение : в In[2] мы воспользовались оператором Do, а в In[4] записали составное выражение; в In[3] и In[5] мы вывели на экран результаты соответствующих вычислений. Результаты в Out[3] и Out[5], как и ожидалось, совпадают.

Рис. 11.8. Многократное вычисление выражения при помощи оператора Do

Второй аргумент функции Do, отвечающий за число и характер повторений, может задаваться точно так же, как и для функции создания списков Table (см. лекцию 3 настоящего курса) и также называется итератором.

Так функция Do[expr,{i,imax}] вычисляет imax выражение expr, при этом expr может содержать символ i, который, в свою очередь, дискретно меняется от 1 до imax с шагом единица. При задании итератора в форме {i,imin,imax} значение символа i с шагом единица меняется от imin до imax. Добавленный в итератор {i,imin,imax,step} четвёртый аргумент step задаёт шаг изменения i. Выражение i может быть любым, но заголовок его не должен быть защищён от присвоения атрибутом Protected. Аргументы итератора imin, imax и step также необязательно должны быть числами, но выражение (imax-imin)/step должно быть числом. В случае, когда imax меньше imin, выражение step может принимать отрицательные значения.

Функция Do является по истине универсальной. На рис. 11.9 продемонстрированы несколько примеров, когда функция Do выполняет роли других встроенных функций Mathematica. В In[1] и In[2] приведён пример, аналогичный примеру в книге Е. М. Воробьёва [1, с. 167], демонстрирующий, что универсальная функция Do порой может заменить функцию суммирования Sum. Здесь же мы впервые задали итератор, содержащий два аргумента: некоторый символ i, входящий в вычисляемое выражение, и количество повторений. Примеры In[3] и In[4] иллюстрируют возможность заменить функцией Do функцию умножения Product. Заданный с тремя аргументами итератор теперь задаёт ещё и нижнюю границу изменения значений символа i. В примере In[5] мы многократно вызываем некоторую неопределённую функцию f, аргументами которой являются результат вычисления этой функции на предыдущем шаге и значение первого аргумента итератора i. При этом i меняется от 2 до 20 с заданным нами интервалом 5.

Подробней о функции Do см. книги Е. М. Воробьёва [1, с. 164–167] и П. Веллина и др. [14, с. 117–120].

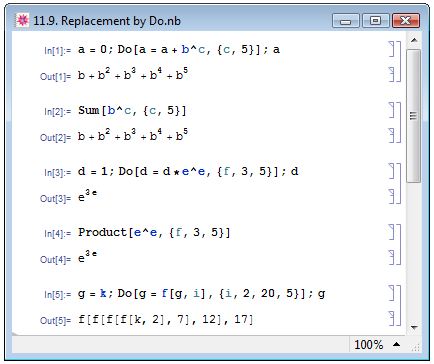
Рис. 11.9. Использование универсальной Do как альтернативы некоторым встроенным функциям Mathematica

11.2.2. Операторы While и NestWhile

Оператор Do[expr,imax] вычисляет выражение или набор выражений expr заранее заданное пользователем число раз imax. Однако может случиться, что заданного количества вычислений оказывается недостаточно для получения требуемого результата, либо заданное количество вычислений избыточно. В этом случае придётся либо вручную изменить количество повторений в исходном цикле, либо задавать ещё один (а то и несколько) цикл Do, выполняющий недостающее количество вычислений.

Ещё один выход из данной ситуации заключается в использовании встроенной функции While. При задании функции в виде While[cond,expr] вычисление начинается с проверки условия cond. Если проверка возвращает значение True, то вычисляется выражение expr. В процессе вычисления expr условие cond должно быть каким-либо образом изменено. На следующем шаге снова проверяется (уже изменённое) условие cond: если вновь возвращается True, то вычисляется и выражение expr. Цикл повторяется до тех пор, пока проверка cond не вернёт значения False (Е. М. Воробьёв [1, с. 171]).

Для иллюстрации эффективности использования функции While при решении некоторых задач воспользуемся изящным примером, приведённым в книге П. Веллина и др. [14, с. 117–119], а именно, зададим средствами Mathematica функцию, которая ищет нули заданной математической функции, используя метод Ньютона (также известный как метод касательных). Метод Ньютона есть итерационный численный метод. Поиск решения осуществляется путём построения последовательных приближений. Для нахождения корня какой-либо функции применяется следующий алгоритм:

1. задаётся начальное приближение x_0;
2. до тех пор, пока не будет достигнут требуемый результат, например, пока не достигнута заданная точность, вычисляется новое приближение по итерационной формуле .

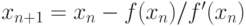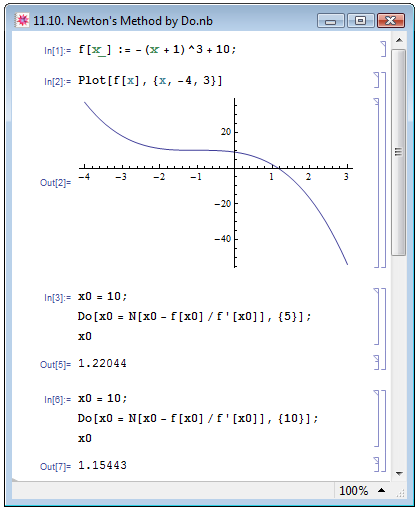
На рис. 11.10 мы по аналогии с примером в книге П. Веллина и др. [14, с.120], реализуем метод Ньютона при помощи оператора Do. Пусть нам необходимо найти нули параболы 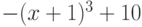. В примере In[1] мы задаём пользовательскую функцию, в теле которой содержатся заданная математическая функция, а аргументом является аргумент математической функции. В In[2] мы для наглядности строим график зависимости нашей математической функции от аргумента x. В In[3] мы последовательно задаём начальное приближение, x0=10, задаём цикл Do, который вычисляет итерационную формулу 5 раз, и выводим полученное после всех итераций значение приближения x0. Именно это значение и напечаталось в Out[5]. Количество итераций (а именно, 5) мы задали случайным образом. Достаточно ли точное значение мы получили в результате вычислений? Не превышает ли погрешность (отличие приближения от истинного значения) хотя бы одной тысячной? Для сравнения проведём вычисление итерационной формулы 10 раз при том же начальном приближении — пример In[6]. Результаты вычислений в Out[5] и Out[7] оказываются значительно отличающимися друг от друга.

Таким образом, при реализации метода Ньютона для нахождения нулей функции при помощи оператора Do мы можем задавать только количество итераций, но не допустимую точность нахождения приближения.

Рис. 11.10. Реализация метода Ньютона для нахождения нулей функции при помощи функции Do

На рис. 11.11 мы, как и П. Веллин и др. [14, с. 124–125], реализовали тот же алгоритм при помощи оператора While. В примере In[2] мы задали цикл While, который повторяет вычисление итерационной формулы до тех пор, пока полученное приближённое вычисление не будет совпадать с истинным с точностью до одной миллионной. Нам не пришлось наугад задавать количество итераций в надежде добиться требуемой точности, Mathematica сделала это самостоятельно.

Ещё более упростить задание алгоритма Ньютона нам позволит функция NestWhile[func,incond,test], которая на каждой итерации вычисляет выражение func при начальных условиях incond до тех пор, пока выполняется условие test.

Вновь воспользуемся примером из книги П. Веллина и др. [14, с. 127–128]. В In[4] на рис. 11.11 мы определяем пользовательскую функцию NMfindRoot, первый аргумент которой — функция, нули которой требуется найти, второй — начальное приближение, и третий — требуемая точность. В In[5] мы опробуем действие вновь определённой пользовательской функции NMfindRoot на всё том же выражении , задав NMfindRoot[f,10,0.000001].

Откроем маленький секрет: находя нули математической функции при помощи FindRoot, Mathematica пользуется именно методом Ньютона. В примере In[6] на рис. 11.11 мы для сравнения находим ноль нашей функции 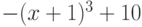при помощи FindRoot.

Подробней о функциях While и NestWhile см. книги Е. М. Воробьёва [1, с. 171–172] и П. Веллина и др. [14, с. 123–128].

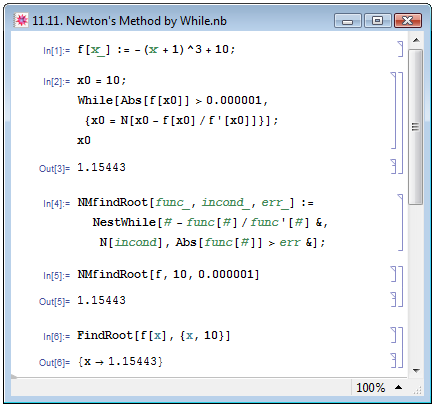
Рис. 11.11. Реализация метода Ньютона для нахождения нулей функции при помощи функций While и NestWhile

11.2.3. Оператор For

Ещё одним условным оператором Mathematica является оператор For. По функционалу он очень похож на оператор While. Заданный в виде For[istart,icond,ichange,expr] он инициирует некоторое начальное выражение istart, а затем многократно вычисляет выражения ichange и expr, пока условие icond возвращает True. Часто istart задаёт начальное значение некоторого счётчика i, icond — условие, которому значение i должно подчиняться, чтобы выражение expr было вычислено, а ichange — выражение, изменяющее значение счётчика i согласно некоторой закономерности.

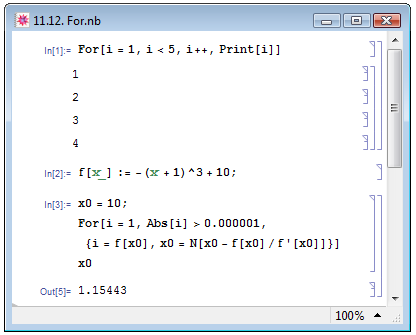
В In[1] на рис. 11.12 представлен простейший пример использования цикла For. Он выводит на экран при помощи выражения Print[i] значение счётчика i, которое меняется от стартового значения i=1 и должно удовлетворять условию i<5. На каждой итерации значение i увеличивается на единицу при помощи выражения i++. Вместо i++ можно задать i=i+1.

В примере In[3] на рис. 11.12 мы задаём алгоритм, реализующий так полюбившийся нам метод Ньютона. Решение этой задачи при помощи оператора For оказалось не менее простым и изящным, чем при помощи While и NestWhile. В этом примере мы немного изменили (упростили) порядок задания аргументов функции For: мы намеренно пропустили отвечающее за изменение значение счётчика выражение ichange, и включили выполняющее его роль выражение i=f[x0] в expr.

Подробней о функции For см. книгу Е. М. Воробьёва [1, с. 172–173].

Рис. 11.12. Задание условных циклов при помощи оператора For