Символьные вычисления
5.1.2. Преобразование рациональных выражений
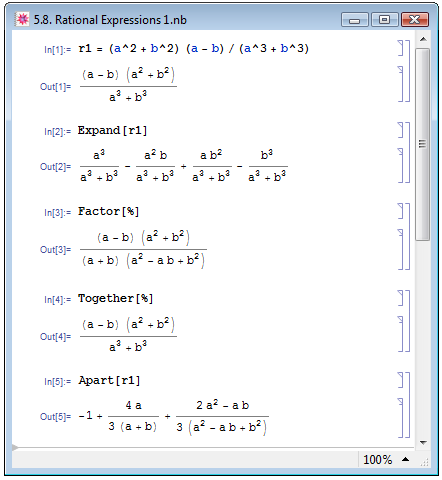
Е. М. Воробьёв [1, с. 40] определяет рациональные выражения следующим образом: "Дробь, числитель и знаменатель которой — полиномы, называется рациональным выражением". Функции Factor и Expand, с которыми мы познакомились выше, также можно применять и к рациональным выражениям. Функция Expand[rexpr] раскрывает числитель и представляет рациональное выражение rexpr в виде суммы дробей, знаменателями которых выступает знаменатель исходного выражения, а числители являются слагаемыми раскрытого числителя — пример In[2] на рис. 5.8. Функция Factor[rexpr] раскладывает на множители и числитель, и знаменатель. Если выражение rexpr является суммой рациональных выражений, то функция Factor[rexpr] приводит все выражения суммы к общему знаменателю и также раскладывает на множители и числитель, и знаменатель — пример In[3] на рис. 5.8.
Ещё одна функция, которая специфическим образом работает с суммой рациональных выражений — Together[rexpr]: она приводит выражения суммы к общему знаменателю и сокращает общие множители — пример In[4] на рис. 5.8.
Новая для нас функция Apart[rexpr] раскладывает рациональное выражение rexpr на сумму простых дробей — пример In[5] на рис. 5.8.
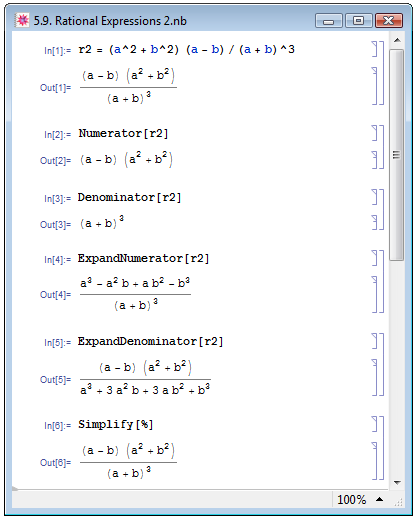
Зачастую может возникнуть необходимость провести преобразования только числителя или только знаменателя дроби. Выделить числитель и знаменатель рационального выражения rexpr позволяют функции Numerator[rexpr] и Denomenator[rexpr], соответственно — примеры In[2] и In[3] на рис. 5.9.
Mathematica позволяет, не извлекая числителя и знаменателя из рационального выражения rexpr, производить их раскрытие: для этого используются функции ExpandNumerator[rexpr] и ExpandDenominator[rexpr], соответственно — примеры In[4] и In[5] на рис. 5.9.
Упрощение выражений (и рациональных в том числе) осуществляется функцией Simplify. Результатом применения этой функции к выражению expr является простейшая с точки зрения Mathematica форма этого выражения — пример In[6] на рис. 5.9.
Подробней о функциях преобразования рациональных выражений см. книгу Е. М. Воробьёва [1, с. 40–42].
5.1.3. Преобразование выражений, содержащих тригонометрические и гиперболические функции
В предыдущих лекциях мы уже познакомились с некоторыми встроенными функциями, которые задают тригонометрические математические функции: это функции нахождения синуса Sin и косинуса Cos. Другие тригонометрические функции в Mathematica: тангенс Tan и котангенс Cot, секанс Sec и косеканс Csc. Обратные тригонометрические функции: арксинус ArcSin и арккосинус ArcCos, арктангенс ArcTan и арккотангенс ArcCot, арксеканс ArcSec и арккосеканс ArcCsc.
Гиперболические функции задаются в Mathematica следующим образом: гиперболические синус Sinh и косинус Cosh, тангенс Tanh и котангенс Coth, секанс Sech и косеканс Csch. Обратные гиперболические функции: гиперболические арксинус ArcSinh и арккосинус ArcCosh, арктангенс ArcTanh и арккотангенс ArcCoth, арксеканс ArcSech и арккосеканс ArcCsch.
По умолчанию в Mathematica углы задаются в радианах. Однако если пользователь хочет оперировать углами, заданными в градусах, программа даёт такую возможность. Чтобы аргумент тригонометрической функции воспринимался как заданный в градусах, к нему справа следует дописать выражение Degree. В In[1] рис. 5.10 аргументы первых двух функций мы задали в радианах, а двух последних — в градусах.
Для преобразования выражений, содержащих тригонометрические и гиперболические функции, в Mathematica имеется целый набор встроенных функций (А. Н. Прокопеня и А. В. Чичурин [5, с. 27–28].
Функция TrigExpand[texpr] избавляет выражение texpr от кратных углов, заменяя тригонометрические и гиперболические функции от них степенями и произведениями функций, а также раскрывает скобки.
Противоположное действие осуществляет функция TrigReduce[expr]: она заменяет произведения и степени тригонометрических и гиперболических функций в expr функциями кратных углов.
Функция TrigFactor[expr] преобразует выражение expr, используя соотношения между тригонометрическими (гиперболическими) функциями.
TrigToExp[expr] записывает тригонометрические и гиперболические функции через экспоненты, а функция ExpToTrig[expr] совершает обратное действие — записывает экспоненту от комплексного аргумента в expr через тригонометрические или гиперболические функции.
Примеры использования функций преобразования выражений, содержащих тригонометрические и гиперболические функции, см. на рис. 5.10.
увеличить изображение
Рис. 5.10. Преобразование выражений, содержащих тригонометрические и гиперболические функции