Работа со списками
Теперь разберёмся в терминологии. В предыдущих лекциях мы уже встречались понятием многоуровневости. Мы говорили о том, что любое выражение во внутреннем представлении являет собой многоуровневую структуру: на нулевом уровне содержится заголовок выражения, на первом — аргументы функции, определяемой заголовком, на втором — аргументы аргументов и так далее. Количество уровней внутренней формы соответствует максимальному номеру уровня в выражении плюс единица, то есть, в него входит и нулевой уровень.
Когда мы говорим о числе уровней списков, мы имеем в виду только те уровни, на которых содержатся элементы списков. Это значит, что ни о каком нулевом уровне списков речи не идёт, и, соответственно, количество уровней списка соответствует максимальному номеру уровня. Здесь также следует отметить, что заголовок списка List является нулевым элементом (но не уровнем!) списка, который он определяет.
Чтобы окончательно запутать читателей, отметим ещё следующее: список, как и всякое выражение, может быть представлен в полной форме. В этом случае следует заранее оговаривать, об уровнях списка или уровнях полной формы представления списка идёт речь.
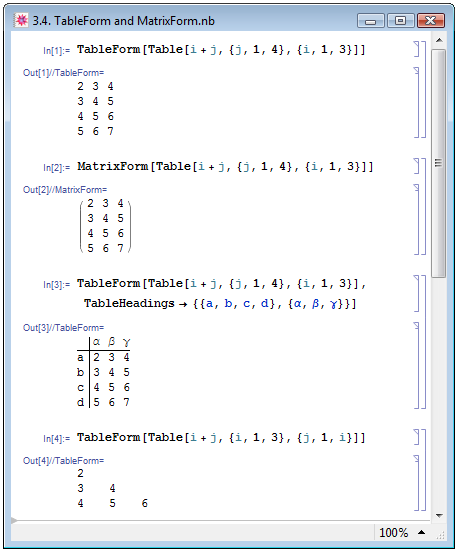
Вложенные списки можно представлять на экране различными способами. С простейшим, "одноэтажным" способом мы уже подробным образом познакомились. Однако такое представление не является достаточно наглядным. Гораздо удобней выводить списки на экран в виде таблицы — функцией TableForm, и матрицы — функцией MatrixForm — см. соответствующие примеры In[1] и In[2] на рис. 3.4. Дополнительная опция TableHeads функции TableForm добавляет заголовки столбцам и строкам таблицы (пример In[3]).
Внешний итератор может зависеть от значения внутреннего итератора (П. Веллин и др. [14, с. 57]), в результате чего могут создаваться непрямоугольные списки — см. пример In[4] на рис. 3.4, в котором количество столбцов в таблице меняется с изменением номера строки. Но внутренний итератор зависеть от внешнего не может, поскольку, как мы видели выше, при генерации списка внутренний итератор должен иметь фиксированное значение, пока изменяется внешний.
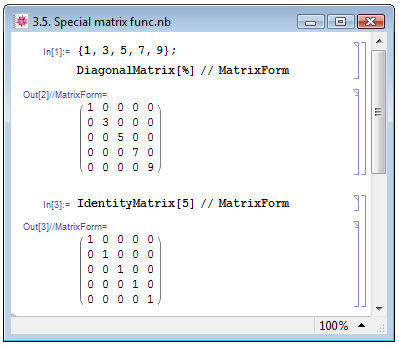
В Mathematica имеется функция DiagonalMatrix[list], позволяющая из заданного списка list порождать новый список, отвечающий диагональной матрице с элементами списка list на главной диагонали. Также имеется функция IdentityMatrix[n], порождающая единичную матрицу размерности n x n. Примеры задания таких матриц см. на рис. 3.5.
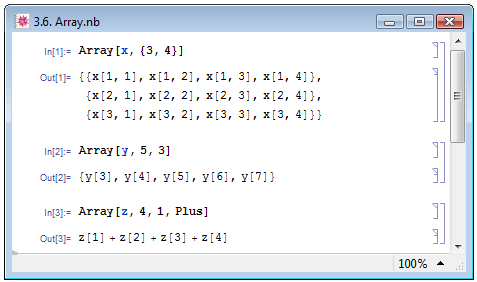
Последним способом задания списков, с которым мы познакомимся в рамках данного курса, является использование функции с заголовком Array. Функция Array[a,n] порождает список длины п с элементами а[i], где i=1,2,...,n. Итератор, заданный в виде {n1,n2,...}, приводит к созданию вложенного списка — см. пример In[1]. Функция Array[a,it,origin] дает список, в котором индексы итераторов it изменяются, начиная со значения origin, по умолчанию равного единице (пример In[2]). Если же функция задана в полной форме, Array[а,it,origin,h], то получается выражение, в котором заголовок List всюду заменен заголовком h — пример In[3] на рис. 3.6.
Подробней о функции Array см. книгу Е. М. Воробьёва [1, с. 103].