Al Simulation
Topics Covered In This Chapter:
"Computer vs. Computer" Games
The Reversi AI algorithm was very simple, but it beats me almost every time I play it. This is because the computer can process instructions very fast, so checking each possible position on the board and selecting the highest scoring move is easy for the computer. If I took the time to look at every space on the board and write down the score of each possible move, it would take a long time for me to find the best move.
Did you notice that our Reversi program in "Caesar Cipher" had two functions, getPlayerMove() and getComputerMove(), which both returned the move selected as a two-item list like [x, y] ? The both also had the same parameters, the game board data structure and which tile they were. getPlayerMove() decided which [x, y] move to return by letting the player type in the coordinates. getComputerMove() decided which [x, y] move to return by running the Reversi AI algorithm.
What happens when we replace the call to getPlayerMove() with a call to getComputerMove() ? Then the player never types in a move, it is decided for them! The computer is playing against itself!
We are going to make three new programs, each based on the Reversi program in the last chapter. We will make changes to reversi.py to create AISim1.py. Next we will make changes to AISim1.py to create AISim2.py. And finally, we will make changes to AISim2.py to for AISim3.py. You can either type these changes in yourself, or download them from the book's website at the URL http://inventwithpython.com/chapter16.
Making the Computer Play Against Itself
Save the old reversi.py file as AISim1.py by clicking on File and then Save As, and then entering AISim1.py for the file name and clicking Ok. This will create a copy of our Reversi source code as a new file that we can make changes to, while leaving the original Reversi game the same (we may want to play it again). Change the following code in AISim1.py:
266. move = getPlayerMove(mainBoard, playerTile)
To this (the change is in bold):
266. move = getComputerMove(mainBoard, playerTile)
And run the program. Notice that the game still asks you if you want to be X or O, but it will not ask you to enter in any moves. When we replaced getPlayerMove(), we no longer call any code that takes this input from the player. We still press Enter after the original computer's moves (because of the input('Press Enter to see the computer\'s move.') on line 285), but the game plays itself!
Let's make some other changes to AISim1.py. All of the functions we defined for Reversi can stay the same. But replace the entire main section of the program (line 246 and on) to look like the following code. Some of the code has remained, but most of it has been altered. But all of the lines before line 246 are the same as in Reversi in the last chapter. You can also avoid typing in the code by downloading the source from the URL http: //inventwithpython.com/chapter 16.
AISim1.py
This code can be downloaded from http://inventwithpython.com/AISim1.py
If you get errors after typing this code in, compare it to the book's code with the online
diff tool at http://inventwithpython.com/diff or email the author at
246. print('Welcome to Reversi!')
247 .
248. while True:
249. # Reset the board and game.
250. mainBoard = getNewBoard()
251. resetBoard(mainBoard)
252. if whoGoesFirst() == 'player':
253 . turn = 'X'
254. else:
255. turn = 'O'
256. print('The ' + turn + ' will go first.')
257 .
258. while True:
259. drawBoard(mainBoard)
260. scores = getScoreOfBoard(mainBoard)
261. print('X has %s points. O has %s points' % (scores['X'] , scores ['O']))
262. input('Press Enter to continue.')
263 .
264. if turn == 'X':
265. # X's turn.
266. otherTile = 'O'
267. x, y = getComputerMove(mainBoard, 'X')
268. makeMove(mainBoard, 'X', x, y)
269 . else:
270. # O's turn.
271. otherTile = 'X'
272. x, y = getComputerMove(mainBoard, 'O')
273. makeMove(mainBoard, 'O', x, y)
274 .
275. if getValidMoves(mainBoard, otherTile) == []:
276. break
277. else:
278. turn = otherTile
279 .
280. # Display the final score.
281. drawBoard(mainBoard)
282. scores = getScoreOfBoard(mainBoard)
283. print('X scored %s points. O scored %s points.' % (scores['X'] , scores ['O']))
284 .
285. if not playAgain() :
286. sys.exit()
How the AISim1 .py Code Works
The AISim1.py program is the same as the original Reversi program, except that the call to getPlayerMove() has been replaced with a call to getComputerMove(). There have been some other changes to the text that is printed to the screen to make the game easier to follow.
When you run the AISim1.py program, all you can do is press Enter for each turn until the game ends. Run through a few games and watch the computer play itself. Since both the X and O players are using the same algorithm, it really is just a matter of luck to see who wins. The X player will win half the time, and the O player will win half the time.
Making the Computer Play Itself Several Times
But what if we created a new algorithm? Then we could set this new AI against the one implemented in getComputerMove(), and see which one is better. Let's make some changes to our program. Click on File and then Save As, and save this file as AISim2.py so that we can make changes without affecting AISim1.py. At this point, AISim1.py and AISim2.py have the same code. We will make changes to AISim2.py and save that file so that AISim2.py has the new changes and AISim1.py has the original code.
Add the following code. The additions are in bold, and some lines have been removed. When you are done changing the file, save it as AISim2.py.
If this is confusing, you can always download the AISim2.py source code from the book's website at http://inventwithpython.com/chapter16.
AISim2.py
This code can be downloaded from http://inventwithpython.com/AISim2.py
If you get errors after typing this code in, compare it to the book's code with the online
diff tool at http://inventwithpython.com/diff or email the author at
246. print('Welcome to Reversi!')
247.
248. xwins = 0
249. owins = 0
250. ties = 0
251. numGames = int(input('Enter number of games to run: '))
252.
253. for game in range(numGames):
254. print('Game #%s:' % (game), end=' ')
255. # Reset the board and game.
256. mainBoard = getNewBoard()
257. resetBoard(mainBoard)
258. if whoGoesFirst() == 'player':
259. turn = 'X'
260. else:
261. turn = 'O' 262 .
263. while True:
264. if turn == 'X':
265. # X's turn.
266. otherTile = 'O'
267. x, y = getComputerMove(mainBoard, 'X')
268. makeMove(mainBoard, 'X', x, y)
269. else:
270. # O's turn.
271. otherTile = 'X'
272. x, y = getComputerMove(mainBoard, 'O')
273. makeMove(mainBoard, 'O', x, y)
274.
275. if getValidMoves(mainBoard, otherTile) == []:
276. break
277. else:
278. turn = otherTile
279.
280. # Display the final score.
281. scores = getScoreOfBoard(mainBoard)
282. print('X scored %s points. O scored %s points.' % (scores['X'], scores['O']))
283.
284. if scores['X'] > scores ['O'] :
285. xwins += 1
286. elif scores['X'] < scores ['O'] :
287. owins += 1
288. else:
289. ties += 1
290.
291. numGames = float(numGames)
292. xpercent = round(((xwins / numGames) * 100), 2)
293. opercent = round(((owins / numGames) * 100), 2)
294. tiepercent = round(((ties / numGames) * 100), 2)
295. print('X wins %s games (%s%%), O wins %s games (%s%%),
ties for %s games (%s%%) of %s games total.' % (xwins, xpercent,
owins, opercent, ties, tiepercent, numGames))
How the AISim2.py Code Works
We have added the variables xwins, owins, and ties to keep track of how many times X wins, O wins, and when they tie. Lines 284 to 289 increment these variables at the end of each game, before it loops back to start a brand new game.
We have removed most of the print() function calls from the program, and the calls to drawBoard() . When you run AISim2.py, it asks you how many games you wish to run. Now that we've taken out the call to drawBoard() and replace the while True: loop with a for game in range(numGames): loop, we can run a number of games without stopping for the user to type anything. Here is a sample run where we run ten games of computer vs. computer Reversi:
Welcome to Reversi! Enter number of games to run: 10 Game #0: X scored 40 points. O scored 23 points. Game #1: X scored 24 points. O scored 39 points. Game #2: X scored 31 points. O scored 30 points. Game #3: X scored 41 points. O scored 23 points. Game #4: X scored 30 points. O scored 34 points. Game #5: X scored 37 points. O scored 27 points. Game #6: X scored 29 points. O scored 33 points. Game #7: X scored 31 points. O scored 33 points. Game #8: X scored 32 points. O scored 32 points. Game #9: X scored 41 points. O scored 22 points. X wins 5 games (50.0%), O wins 4 games (40.0%), ties for 1 games (10.0%) of 10.0 games total.
Because the algorithm does have a random part, your run might not have the exact same numbers as above.
Printing things out to the screen slows the computer down, but now that we have removed that code, the computer can run an entire game of Reversi in about a second or two. Think about it. Each time our program printed out one of those lines, it ran through an entire game (which is about fifty or sixty moves, each move carefully checked to be the one that gets the most points).
Percentages
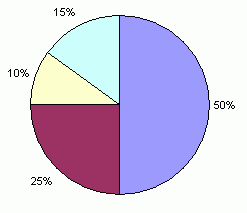
Percentages are a portion of a total amount, and range from 0% to 100%. If you had 100% of a pie, you would have the entire pie. If you had 0% of a pie, you wouldn't have any pie at all. 50% of the pie would be half of the pie. A pie is a common image to use for percentages. In fact, there is a kind of chart called a pie chart which shows how much of the full total a certain portion is. Here is a pie chart with 10%, 15%, 25%, and 50% portions below. Notice that 10% + 15% + 25% + 50% adds up to 100%.
We can calculate the percentage with division. To get a percentage, divide the part you have by the total, and then multiply by one hundred. For example, if X won 50 out of 100 games, you would calculate the expression 50 / 100, which would evaluate to 0.5. We multiply this by 100 to get a percentage (in this case, 50%). Notice that if X won 100 out of 200 games, we could calculate the percentage with 100 / 200, which would also evaluate to 0.5. When we multiply 0.5 by 100 to get the percentage, we get 50%. Winning 100 out of 200 games is the same percentage (that is, the same portion) as winning 50 out of 100 games.
Division Evaluates to Floating Point
It is important to note that when you use the / division operator, the expression will always evaluate to a floating point number. For example, the expression 10 / 2 will evaluate to the floating point value 5.0 and not to the integer value 5.
This is important to remember, because adding an integer to a floating point value with the + addition operator will also always evaluate to a floating point value. For example, 3 + 4.0 will evaluate to the floating point value 7.0 and not to the integer 7.
Try entering the following code into the interactive shell:
>>> spam = 100 / 4 >>> spam 25.0 >>> spam = spam + 20 >>> spam 45.0 >>>
Notice that in the above example, the data type of the value stored in spam is always a floating point value. You can pass the floating point value to the int() function, which will return an integer form of the floating point value. But this will always round the floating point value down. For example, the expressions int(4.0), int(4.2), and int(4.9) will all evaluate to 4, and never 5.