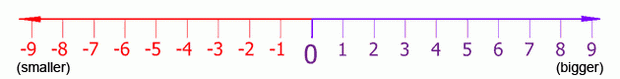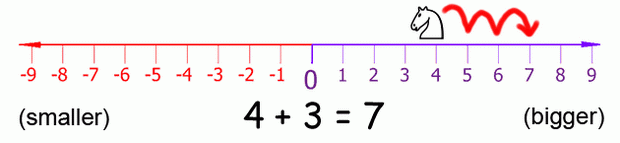Cartesian Coordinates
Topics Covered In This Chapter:
- Cartesian coordinate systems.
- The X-axis and Y-axis.
- The Commutative Property of Addition.
- Absolute values and the abs() function.
This chapter does not introduce a new game, but instead goes over some simple mathematical concepts that we will use in the rest of the games in this book.
When you look at 2D games (such as Tetris or old Super Nintendo or Sega Genesis games) you can see that most of the graphics on the screen can move left or right (the first dimension) and up or down (the second dimension, hence 2D). In order for us to create games that have objects moving around two dimensions (such as the two dimensional computer screen), we need a system that can translate a place on the screen to integers that our program can deal with.
This is where Cartesian coordinate systems come in. The coordinates can point to a very specific point on the screen so that our program can keep track of different areas on the screen.
Negative numbers are often used with Cartesian coordinate systems as well. The second half of this chapter will explain how we can do math with negative numbers.
You may already know about Cartesian coordinate systems and negative numbers from math class. In that case, you can just give this chapter a quick read anyway to refresh yourself.
Grids and Cartesian Coordinates
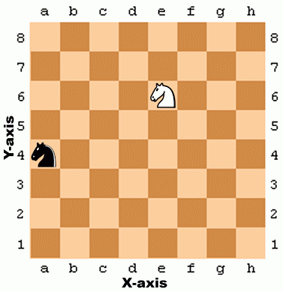
A problem in many games is how to talk about exact points on the board. A common way of solving this is by marking each individual row and column on a board with a letter and a number. Figure 12.1 is a chess board that has each row and each column marked.
In chess, the knight piece looks like a horse head. The white knight is located at the point e, 6 and the black knight is located at point a, 4. We can also see that every space on row 7 and every space in column c is empty.
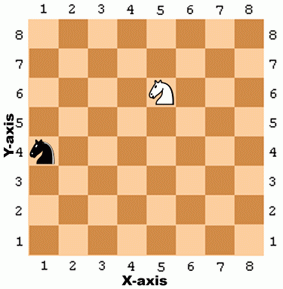
A grid with labeled rows and columns like the chess board is a Cartesian coordinate system. By using a row label and column label, we can give a coordinate that is for one and only one space on the board. This can really help us describe to a computer the exact location we want. If you have learned about Cartesian coordinate systems in math class, you may know that usually we have numbers for both the rows and columns. This is handy, because otherwise after the 26th column we would run out of letters. That board would look like Figure 12.2.
The numbers going left and right that describe the columns are part of the X-axis. The numbers going up and down that describe the rows are part of the Y-axis. When we describe coordinates, we always say the X-coordinate first, followed by the Y-coordinate. That means the white knight in the above picture is located at the coordinate 5, 6 (and not 6, 5). The black knight is located at the coordinate 1, 4 (not to be confused with 4, 1).
Notice that for the black knight to move to the white knight's position, the black knight must move up two spaces, and then to the right by four spaces. (Or move right four spaces and then move up two spaces.) But we don't need to look at the board to figure this out. If we know the white knight is located at 5, 6 and the black knight is located at 1, 4, then we can just use subtraction to figure out this information.
Subtract the black knight's X-coordinate and white knight's X-coordinate: 5 - 1 = 4. That means the black knight has to move along the X-axis by four spaces.
Subtract the black knight's Y-coordinate and white knight's Y-coordinate: 6 - 4 = 2. That means the black knight has to move along the Y-axis by two spaces.
Negative Numbers
Another concept that Cartesian coordinates use is negative numbers. Negative numbers are numbers that are smaller than zero. We put a minus sign in front of a number to show that it is a negative number. -1 is smaller than 0. And -2 is smaller than -1. And -3 is smaller than -2. If you think of regular numbers (called positive numbers) as starting from 1 and increasing, you can think of negative numbers as starting from -1 and decreasing. 0 itself is not positive or negative. In this picture, you can see the positive numbers increasing to the right and the negative numbers decreasing to the left:
The number line is really useful for doing subtraction and addition with negative numbers. The expression 4 + 3 can be thought of as the white knight starting at position 4 and moving 3 spaces over to the right (addition means increasing, which is in the right direction).
As you can see, the white knight ends up at position 7. This makes sense, because 4 + 3 is 7.
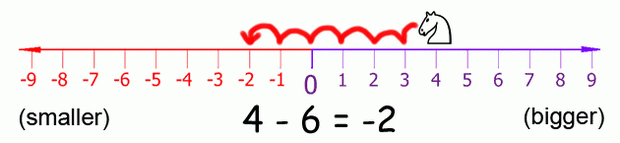
Subtraction can be done by moving the white knight to the left. Subtraction means decreasing, which is in the left direction. 4 - 6 would be the white knight starting at position 4 and moving 6 spaces to the left:
The white knight ends up at position -2. That means 4 - 6 equals -2.
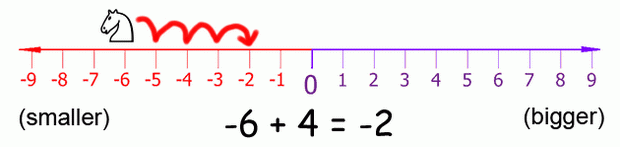
If we add or subtract a negative number, the white knight would move in the opposite direction. If you add a negative number, the knight moves to the left. If you subtract a negative number, the knight moves to the right. The expression -6 - -4 would be equal to -2. The knight starts at -6 and moves to the right by 4 spaces. Notice that -6 - -4 has the same answer as -6 + 4.
увеличить изображение
Рис. 12.6. Even if the white knight starts at a negative coordinate, moving right still adds to the coordinate.
The number line is the same as the X-axis. If we made the number line go up and down instead of left and right, it would model the Y-axis. Adding a positive number (or subtracting a negative number) would move the knight up the number line, and subtracting a positive number (or adding a negative number) would move the knight down. When we put these two number lines together, we have a Cartesian coordinate system like in Figure 12.7.