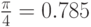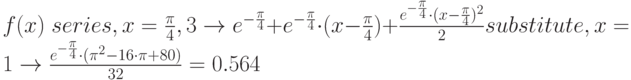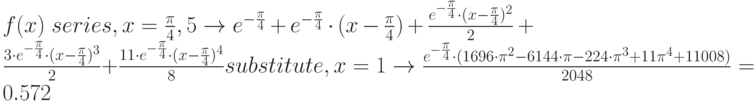Математические методы в моделировании экономики
Вычисление пределов
Для нахождения предела функции Mathcad используется панель Calculus. Ввести функцию под знак 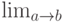 . Обязательно выделить его (клавиша "пробел"), щелкнуть оператор символьного вывода (панель Symbolic или Evaluation).
. Обязательно выделить его (клавиша "пробел"), щелкнуть оператор символьного вывода (панель Symbolic или Evaluation).
Предел функции в точке  – это число
– это число  , к которому сходится последовательность значений функции для любой сходящейся к значению а последовательности значений аргумента. При моделировании поведения экономического показателя определение предела функции при неограниченном росте задаваемого фактора или при его стремлении к определенному значению дает информацию, какое значение может иметь исследуемый показатель.
, к которому сходится последовательность значений функции для любой сходящейся к значению а последовательности значений аргумента. При моделировании поведения экономического показателя определение предела функции при неограниченном росте задаваемого фактора или при его стремлении к определенному значению дает информацию, какое значение может иметь исследуемый показатель.
Пример 1.6.
В теории потребления исследуется распределение доходов населения между разными видами расходов. Функции спроса описывают зависимость спроса на товары определенной категории от размера поучаемого дохода. Известны функции Торнквиста, которые описывают зависимость величины спроса на различные группы товаров в зависимости от их роли в процессе потребления. Пределы функций при неограниченном росте доходов показывают насыщение спроса в каждом случае. Пусть  –спрос,
–спрос,  – доход,
– доход, 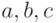 – фиксированные параметры. Функции Торнквиста:
– фиксированные параметры. Функции Торнквиста:
- спрос на малоценные товары:
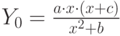
( 1.7) - спрос на товары первой необходимости:

( 1.8) - спрос на товары второй необходимости (более дорогие):
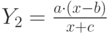
( 1.9) - спрос на товары роскоши:
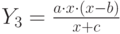
( 1.10)
Примеры вычислений пределов при исследовании спроса на различные виды товаров показаны на рисунке 1.4.
Функции Торнквиста
Спрос на различные виды товаров
 ,
, 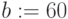 ,
, 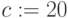
Малоценные товары:
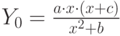
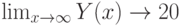
Товары первой необходимости
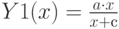
 - При увеличении дохода – насыщение
- При увеличении дохода – насыщение
Товары длительного пользования, спрос возникает лишь с некоторого высокого уровня дохода



Товары роскоши. Спрос растет неограниченно
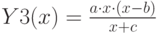
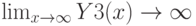
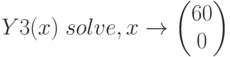
Разложение функции в ряд Тейлора
Разложение функций в степенной ряд Тейлора широко используется и имеет огромное значение при проведении моделирования и математических расчетов. При вычислении интегралов, решении уравнений, оценки значений в окрестности исследуемой точки непосредственное использование некоторых функций может быть сопряжено со значительными трудностями, замена функции степенным рядом позволяет значительно упростить задачу. Приближенная оценка значений исследуемых сложных функций в окрестности точки, представляющей интерес, может быть сведена к нахождению значений соответствующих им многочленов Тейлора.
В Mathcad задача разложения функции  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 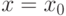 решается символьной операцией с использованием ключевого слова series панели Simbolic. После ключевого слова вводится значение точки разложения с логическим равенством и порядок остаточного члена минус единица.
решается символьной операцией с использованием ключевого слова series панели Simbolic. После ключевого слова вводится значение точки разложения с логическим равенством и порядок остаточного члена минус единица.
Если функция  имеет в точке
имеет в точке 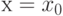 и некоторой ее окрестности производные порядка до
и некоторой ее окрестности производные порядка до 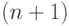 включительно, то функцию можно разложить в ряд Тейлора для любого значения
включительно, то функцию можно разложить в ряд Тейлора для любого значения  этой окрестности
этой окрестности
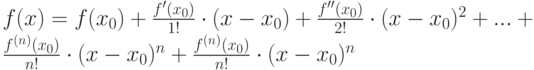 |
( 1.11) |
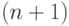 член разложения:
член разложения:
 |
( 1.12) |
Пример. 1.7.
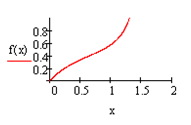
На рисунке 1.5 показан пример разложения функции 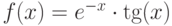 в ряд Тейлора в окрестности точки (
в ряд Тейлора в окрестности точки ( ) с остаточным членом 3, 4 и 5 порядка. Для сравнения рассчитаны значения функции в точке
) с остаточным членом 3, 4 и 5 порядка. Для сравнения рассчитаны значения функции в точке 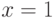 по степенным формулам с разным порядком разложения. Точность до второго знака позволяет ограничиться 4 членами разложения.
по степенным формулам с разным порядком разложения. Точность до второго знака позволяет ограничиться 4 членами разложения.
Следует отметить, запись символьной операции с ключевыми словами 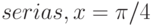 (разложить в точке (
(разложить в точке ( ) и
) и  (подставить
(подставить 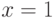 ) идет в одну строку и не переносится. Рисунок листинга является демонстрационным.
) идет в одну строку и не переносится. Рисунок листинга является демонстрационным.
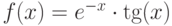
 ,
,