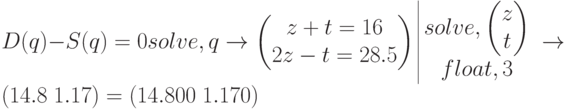Математические методы в моделировании экономики
Интегрирование
Аналитический способ нахождения интеграла - нахождение первообразной для подынтегральной функции, процедура, обратная дифференцированию. В Mathcad интегрирование производится символьным вычислением. Для проведения операции надо под знак 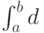 ,(панель Calculus), ввести функцию, пределы интегрирования, переменную, щелкнуть оператор символьного вывода (панель Symbolic или Evaluation). Можно решать: неопределённые и определенные, двойные и тройные интегралы.
,(панель Calculus), ввести функцию, пределы интегрирования, переменную, щелкнуть оператор символьного вывода (панель Symbolic или Evaluation). Можно решать: неопределённые и определенные, двойные и тройные интегралы.
В процессе решения экономических задач приходится производить вычисление накопительного итога: определение суммарного расходования материалов, энергии, прибыли, затрат и т.д. В статистических задачах операция интегрирования требуется при построении интегральных функций распределения по плотности распределения вероятности, при расчете математического ожидания, дисперсии.
Пример 1.2.
Случайная величина задана плотностью распределения 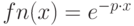 . Определить математическое ожидание и вероятность для случайной величины принять значение от 0,5 до 1.
. Определить математическое ожидание и вероятность для случайной величины принять значение от 0,5 до 1.
Математическое ожидание  выражается соотношением:
выражается соотношением:
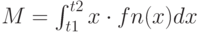 |
( 1.2) |
вероятность  для случайной величины принять значение от
для случайной величины принять значение от  до
до  имеет вид
имеет вид
 |
( 1.3) |
Расчет математического ожидания и вероятности приведен ниже:
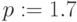
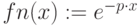 - плотность распределения
- плотность распределения
 - математическое ожидание
- математическое ожидание
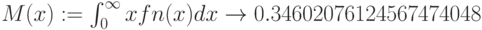
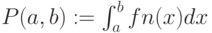 - вероятность принять значение от
- вероятность принять значение от  до
до 
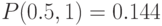 - вероятность принять значение от 0.5 до 1
- вероятность принять значение от 0.5 до 1
Пример 1.3.
Производительность труда от времени  характеризуется функцией
характеризуется функцией
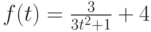 |
( 1.4) |
Определить объем продукции  , произведенной рабочим за первый час и за третий час рабочего дня.
, произведенной рабочим за первый час и за третий час рабочего дня.
Для 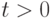 функция
функция  непрерывна. Тогда объем продукции
непрерывна. Тогда объем продукции  , произведенной рабочим за промежуток времени от
, произведенной рабочим за промежуток времени от 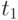 до
до 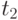 будет иметь вид
будет иметь вид
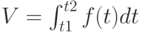 |
( 1.5) |
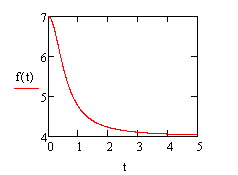
На рисунке 1.2 представлено решение в Mathcad.
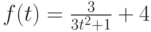
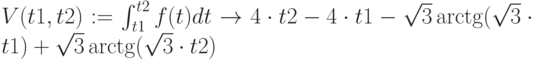 |
( 1.5) |
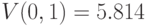 - объем произведенной продукции за первый рабочий час
- объем произведенной продукции за первый рабочий час
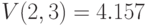 - объем произведенной продукции за третий рабочий час
- объем произведенной продукции за третий рабочий час
Решение уравнений
Техника символьных вычислений позволяет решать уравнения аналитически (в символьном виде). Применяя ключевое слово Solve панели Simbolyc, можно решать уравнения и системы линейных и нелинейных уравнений. Для этого надо ввести уравнения, с использованием логического равенства  с панели Boolean, ключевое слово Solve, переменные, относительно которых решается уравнение.
с панели Boolean, ключевое слово Solve, переменные, относительно которых решается уравнение.
Решение уравнений – ключевой момент математического моделирования. Особенно ценна возможность аналитического решения, это позволяет выразить одни показатели через другие. Рассмотрим примеры.
Пример 1.4.
Обратимся к финансовым вычислениям, которые подробно будут рассмотрены во 2 лекции. По схеме сложных процентов для элементарного денежного потока выражение для будущей стоимости 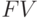 от ставки
от ставки  , текущей стоимости
, текущей стоимости 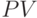 , количества лет
, количества лет  и количества начислений процентов
и количества начислений процентов  в течение года имеет вид:
в течение года имеет вид:
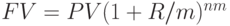 |
( 1.6) |
Для вывода выражений для финансовых параметров 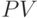 ,
,  ,
,  надо это уравнение решить относительно соответствующего параметра . Решение показано ниже:
надо это уравнение решить относительно соответствующего параметра . Решение показано ниже:
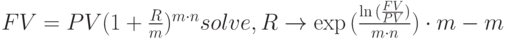
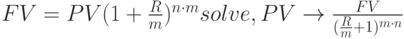

Пример 1.5.
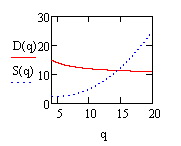
Рассмотрим экономическую задачу изучения спроса и предложения товара на рынке. Спрос на товар  (demand) – сложившаяся на данный момент времени зависимость между ценой спроса товара
(demand) – сложившаяся на данный момент времени зависимость между ценой спроса товара  (price) и количеством товара
(price) и количеством товара  (объемом его покупки). Пусть
(объемом его покупки). Пусть 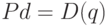 – функция спроса,
– функция спроса,  -цена товара, по которой покупается количество товара
-цена товара, по которой покупается количество товара  . Чем меньше цена, тем больше спрос при постоянной покупательной способности, функция .
. Чем меньше цена, тем больше спрос при постоянной покупательной способности, функция . 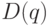 – функция убывающая. Предложение
– функция убывающая. Предложение  (supply) определяется ценой, по которой количество товара
(supply) определяется ценой, по которой количество товара  предлагается на рынке.
предлагается на рынке.  - функция предложения,
- функция предложения, 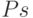 - цена товара, по которой предлагается на продажу количество товара
- цена товара, по которой предлагается на продажу количество товара  , предложение растет с увеличением цены на товар,
, предложение растет с увеличением цены на товар, 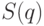 – функция возрастающая. Для экономики представляет интерес условие равновесия, когда спрос равен предложению; это условие дается уравнением
– функция возрастающая. Для экономики представляет интерес условие равновесия, когда спрос равен предложению; это условие дается уравнением 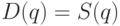 .
.
Пусть функции имеют вид: 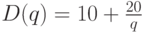
На рисунке 1.3 представлено решение.
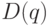 – цена, по которой приобретается количество товара
– цена, по которой приобретается количество товара 
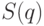 – цена, по которой предлагается количество товара
– цена, по которой предлагается количество товара 
 - количество товара, приобретенного по цене
- количество товара, приобретенного по цене
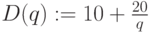
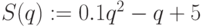

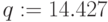
 ,
,  – равновесная цена
– равновесная цена
Следует заметить, Mathcad 14 дат решение уравнения для всей области значений (действительные и комплексные), ключевое слово assume (ограничение для переменной) не работает.
Если имеем систему уравнений, уравнения следует вводить как элементы матрицы.