НОУ ИНТУИТ | Введение в Octave. Лекция 12: Обработка результатов эксперимента. Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 576 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

12.1.3 Полином Лагранжа

Ещё одно представление интерполяционного полинома степени предложил Лагранж:

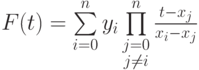$F(t)=\sum \limits_{i=0}^ny_i\prod\limits_{\substack{j=0\\j\not=i}}^n\frac{t-x_j}{x_i-x_j}$

( 12.6)

Напомним читателю, что рассмотренные три способа построения полинома — это три различных формы записи одной и той же функции.

Совет. Полином Лагранжа лучше использовать, если необходимо вычислить значение в небольшом количестве точек. Для расчёта во многих точках рационально использовать полином Ньютона, в котором, можно один раз вычислить значения коэффициентов A_i , после чего можно рассчитать ожидаемое значение в точках по формуле (12.5). При использовании канонического полинома приходится решать систему линейных алгебраических уравнений (12.4), поэтому он используется значительно реже.

12.1.4 Реализация интерполяционного полинома n-й степени

Построить интерполяционный полином -й степени в Octave можно одним из следующих способов:

Средствами языка программирования реализовать один из рассмотренных алгоритмов построения полинома: канонический (см. листинг 12.1), полином Ньютона (см. листинг 12.2), полином Лагранжа (см. листинг 12.3), после чего посчитать значения в нужных точках.
Воспользоваться функцией (в этом случае k = length(x) -1) для вычисления коэффициентов полинома, после чего с помощью функции вычислить значение полинома в необходимых точках.

	
% x — массив абсцисс экспериментальных точек, y — массив ординат
% экспериментальных точек, t — точка в которой требуется найти значение.
function s=kanon(x, y, t)
	n=length(x); % Вычисление количества точек в массивах x и y
% Формирование коэффициентов системы уравнений (12.4)
	for i =1:n
		for j =1:n
			A(i, j)=x(i).^(j-1);
		end
	end
	a=A^(-1)-y’; % Решение системы уравнений (12.4)
	% Вычисление значения полинома в точке t по формуле (12.3)
	s =0;
	for i =1:n
		s=s+a(i)-t^(i-1);
	end
end

Листинг 12.1. Функция kanon для вычисления канонического полинома в точке t по экспериментальным значениям (xi,yi)

	
% x — массив абсцисс экспериментальных точек, y — массив ординат
% экспериментальных точек, t — точка в которой требуется найти значение.
function s=newton(x, y, t)
	n=length(x); % Вычисление количества точек в массивах x и y
	% Запись в первый столбец матрицы разделённых разностей вектора y
	for i =1:n
		C(i, 1)=y(i);
	end
	for i =2:n % Формирование матрицы разделённых разностей
		for j =2:n
			if(i<j)
				C(i, j)=0;
			else
				C(i, j)=(C(i, j-1)-C(j-1, j-1))/(x(i)-x(j-1));
			end
		end
	end
	for i =1:n % Формирование массива коэффициентов полинома Ньютона
		A(i)=C(i, i);
	end
	s =0; % Расчёт значения полинома в точке t по формуле (12.5)
	for i =1:n
		p=1;
		for j =1: i-1
			p=p-(t-x(j));
		end
		s=s+A(i)-p;
	end
end

Листинг 12.2. Функция newton для вычисления полинома Ньютона в точке t по экспериментальным значениям (xi, yi)

Таблица 12.2. Данные к примеру 12.1
x	0.43	0.48	0.55	0.62	0.7	0.75
y	1.63597	1.73234	1.87686	2.03345	2.22846	2.35973

	
% x — массив абсцисс экспериментальных точек, y — массив ординат
% экспериментальных точек, t — точка в которой требуется найти значение.
function s=lagrang(x, y, t)
	n=length(x); % Вычисление количества точек в массивах x и y
	% Расчёт суммы произведений по формуле (12.6)
	% для вычисления значения полинома Лагранжа в точке t
	s =0;
	for i =1:n
		p=1;
			for j =1:n
			if(j~=i)
				p=p-(t-x(j))/(x(i)-x(j));
			end
		end
		s=s+y(i)-p;
	end
end

Листинг 12.3. Функция lagrang для вычисления полинома Лагранжа в точке t по экспериментальным значениям (xi, yi)

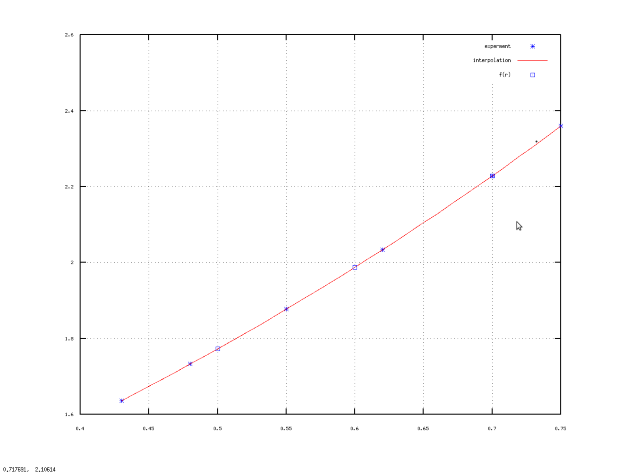
Пример 12.1. В результате эксперимента получена табличная зависимость y(x) (см. табл. 12.2). Построить интерполяционный полином. Вычислить ожидаемое значение в точках 0.5, 0.6 и 0.7, построить график зависимости.

Решение с подробными комментариями представлено в листинге 12.4 Как и следовало ожидать, все четыре используемых метода построения интерполяционного полинома пятой степени дали одни и те же значения.

На рис. 12.1 представлено графическое решение примера 12.1. Подобным образом можно подбирать коэффициенты интерполяционного полинома и для других задач.

	
function s=kanon(x, y, t)
	n=length(x); % Вычисление количества точек в массивах x и y
	for i =1:n % Формирование коэффициентов системы уравнений (12.4)
		for j =1:n
			A(i, j)=x(i).^(j-1);
		end
	end
	a=A^(-1)-y’; % Решение системы уравнений (12.4)
	s =0; % Вычисление значения полинома в точке t по формуле (12.3)
	for i =1:n
		s=s+a(i)-t^(i-1);
	end
end
function s=newton(x, y, t)
	n=length(x); % Вычисление количества точек в массивах x и y
	for i=1:n % Запись в первый столбец C разделённых разностей y
		C(i, 1)=y(i);
	end
	for i =2:n % Формирование матрицы разделённых разностей
		for j =2:n
			if(i<j)
				C(i, j)=0;
			else
				C(i, j)=(C(i, j-1)-C(j-1, j-1))/(x(i)-x(j-1));
			end
		end
	end
	for i =1:n % Формирование массива коэффициентов полинома Ньютона
		A(i)=C(i, i);
	end
	s =0; % Расчёт значения полинома в точке t по формуле (12.5)
	for i =1:n
		p=1;
		for j =1:i-1
			p=p-(t-x(j));
		end
		s=s+A(i)-p;
	end
end
function s=lagrang(x, y, t)
	n=length(x); % Вычисление количества точек в массивах x и y
	s =0; % Расчёт значения полинома Лагранжа в точке t по формуле (12.6)
	for i=1:n
		p=1;
		for j=1:n
			if(j~=i)
				p=p-(t-x(j))/(x(i)-x(j));
			end
		end
		s=s+y(i)-p;
	end
end
% x и y — массивы абсцисс и ординат экспериментальных точек примера 12.1.
x =[0.43 0.48 0.55 0.62 0.7 0.75];
y =[1.63597 1.73234 1.87686 2.03345 2.22846 2.35973];
r = [0.5 0.6 0.7] % точки для которых надо вычислить ожидаемые значения
for i=1:3
% Вычисление i-го ожидаемого значения интерполяционного полинома Ньютона
	rsn(i)=newton(x, y, r(i));
% Вычисление i-го значения канонического интерполяционного полинома
	rsk(i)=kanon(x, y, r(i));
% Вычисление i-го значения интерполяционного полинома Лагранжа
	rsl(i)=lagrang(x, y, r(i));
end
rsn
rsk
rsl
% Вычисление ожидаемых значений интерполяционного полинома в
% точках r = [0.5 0.6 0.7] с помощью функции polyfit
A=polyfit(x, y, length(x)-1)
rsp=polyval(A, r)
% Вычисление точек для построения графика интерполяционного полинома.
x1=0.43:0.01:0.75; y1=polyval(A, x1);
% Построение графика.
plot(x, y, ’*b;experment;’, x1, y1, ’-r;interpolation;’, r, rsp, ’pb;f
	(r);’);
grid();
% Результаты вычислений
r = 0.50000 0.60000 0.70000
rsn = 1.7725 1.9874 2.2285
rsk = 1.7725 1.9874 2.2285
rsl = 1.7725 1.9874 2.2285
A = 0.44180 -1.17180 1.70415 -0.18866 1.38721 0.97243
rsp = 1.7725 1.9874 2.2285

Листинг 12.4. Решение примера 12.1

увеличить изображение
Рис. 12.1. Полиномиальная интерполяция (пример 12.1)

Полиномиальная интерполяция не всегда даёт удовлетворительные результаты при аппроксимации зависимостей. При представлении полиномами возможна большая погрешность на концах этих кривых. Несмотря на выполнение условий в узлах, интерполяционная функция может иметь значительное отклонение от аппроксимируемой кривой между узлами. При этом повышение степени интерполяционного полинома приводит не к уменьшению, а к увеличению погрешности. Решение этой проблемы предложено теорией сплайнинтерполяции (от английского слова spline — рейка, линейка).

Дальше >>

Авторизоваться

Введение в Octave

Обработка результатов эксперимента. Интерполяция функций

12.1.3 Полином Лагранжа

12.1.4 Реализация интерполяционного полинома n-й степени

Вопросы и ответы