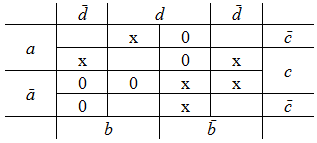Минимизация логических функций
Пример 3.8. Получить методом диаграмм Вейча минимальную дизъюнктивную нормальную форму неполностью определенной ФАЛ, заданной в следующем виде:
f(a,b,c,d) = ?(0,5,8,12,15), Х(1,2,3,10.13,14),
где под знаком X перечислены номера наборов, на которых значение функции не определено.
Решение
Прежде всего, отметим, что при решении данной задачи, так же, как и ранее, необходимо покрыть все 1 клетки минимальным числом прямоугольников максимальной площади. Если клетки с неопределенными значениями способствуют достижению этой цели, то они трактуются как 1-клетки, в противном случае – как 0-клетки.
Для получения минимальной ДНФ вначале на диаграмме Вейча отметим на все 1 клетки и клетки с неопределенными значениями логической функции:
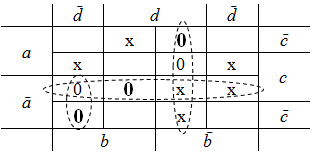
Отметим существенные имликанты для данной функции, принимая клетки с неопределенными значениями за 1-клетки, если это способствует построению покрытия меньшего ранга:
Импликанты в столбце  нельзя в полной мере считать существенными, так как для каждой из них можно подобрать два равнозначных покрытия, но именно приставленное на диаграмме выше позволяет покрыть их обе сразу. Здесь мы сталкиваемся с ситуацией некоторого эвристического перебора, о котором говорилось выше и который во многом зависит от опыта разработчика.
нельзя в полной мере считать существенными, так как для каждой из них можно подобрать два равнозначных покрытия, но именно приставленное на диаграмме выше позволяет покрыть их обе сразу. Здесь мы сталкиваемся с ситуацией некоторого эвристического перебора, о котором говорилось выше и который во многом зависит от опыта разработчика.
Оставшаяся непокрытой одна 1-клетка может быть включена в два равноценных покрытия:
Это даст тупиковую (она же и минимальная) нормальную форму:

Другой вариант покрытия этой 1-клетки даст следующую минимальную дизъюнктивную нормальную форму:
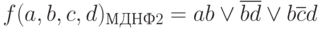
Теперь получим МКНФ этой же функции. Для этого удобнее сначала представить сокращенную запись ее совершенной конъюнктивной нормальной формы:
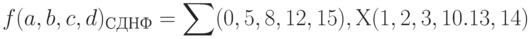
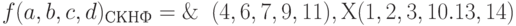
Отметим на диаграмме Вейча все 0-клетки и клетки с неопределенными значениями функции:
Выделим на диаграмме существенные имлиценты:
Так как все покрытия, использованные для покрытия существенных имплицент, покрыли и все остальные имплиценты данной функции, то эта ФАЛ будет иметь единственную минимальную КНФ:
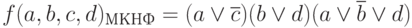
Отметим, что значения функции в неопределенных клетках при получении минимальной дизъюнктивной и минимальной конъюнктивной нормальной форм не связаны между собой. Так, например, значение Х-клетки с координатами  было принято равным единице при получении минимальной дизъюнктивной нормальной формы и, в то же время, равной нулю при получении минимальной конъюнктивной нормальной формы.
было принято равным единице при получении минимальной дизъюнктивной нормальной формы и, в то же время, равной нулю при получении минимальной конъюнктивной нормальной формы.
Х-клетки, которые не способствовали получению наилучшего покрытия 1-клеток при получении МДНФ, принимаем за 0-клетки. Аналогично, Х-клетки, которые не способствовали получению наилучшего покрытия 0-клеток при получении МКНФ, принимаем за 1 клетки.Так для рассматриваемой функции при получении МДНФ Х-клетку с координатами  при получении МДНФ мы рассматриваем как 1-клетку, а при получении МКНФ – как 0-клетку.
при получении МДНФ мы рассматриваем как 1-клетку, а при получении МКНФ – как 0-клетку.
Краткие итоги
В лекции рассмотрены различные методы минимизации логических функций: на основе теоремы Квайна, метода Квайна – Мак-Класки, диаграмм Вейча, не полностью определенных логических функций, которые могут быть использованы как для небольшого (три-четыре) числа переменных непосредственно разработчиками несложных вычислительных устройств, так и для минимизации ФАЛ от произвольного числа аргументов с использованием разнообразных компьютерных алгоритмов.
Вопросы и задания
- Перечислите и охарактеризуйте методы минимизации логических функций.
- Укажите преимущества и недостатки различных методов минимизации логических функций.
- Дайте формулировку теоремы Квайна. Позволяет ли теорема Квайна минимальную форму записи логической функции?
- По какому критерию определяется минимальная логическая функция? Возможны ли другие критерии определения минимальной ФАЛ? Если да, то сформулируйте их.
- Можно ли утверждать, что для того, чтобы получить минимальную конъюнктивную нормальную форму какой-либо логической функции, достаточно получить инверсию от ее минимальной дизъюнктивной нормальной формы?
- Какие из видов функции имеют единственное представление: совершенная форма, сокращенная, тупиковая, минимальная?
- Что представляют собой импликантные и имплицентные матрицы? Для каких целей они используются?
- Какие усовершенствования внес Мак-Класки в минимизацию логических функций?
- С какой целью в методе Квайна – Мак-Класки двоичные наборы разбиваются на группы по количеству единиц в наборе? Какую роль играют "пустые" группы в этом методе?
- Каковы области применения при минимизации диаграмм Вейча и метода Квайна – Мак-Класки? Почему?
- Почему машинные алгоритмы минимизации логических функций обычно базируются на методе Квайна – Мак-Класки?
- Приведите примеры ситуаций, при которых образуются не полнолностью определенные логические функции?
- Как выполнить минимизацию не полностью определенной ФАЛ методом Квайна – Мак-Класки?