Анализ функционирования систем
8.2. Примеры анализа функционирования систем.
Функционирование естественных неживых систем (Солнечная система, атом) — это воспроизводство внутренних отношений. Функционирование естественных живых систем (организм) — это поддержание некоторого уровня внутренних отношений (гомеостазис). Приведем примеры анализа функционирования искусственных систем.
* ПРИМЕР 1. Анализ функционирования автоматической системы управления [120, 204].
Автоматические системы управления (САУ) являются предметом исследования частно-научной теории автоматического управления (ТАУ).
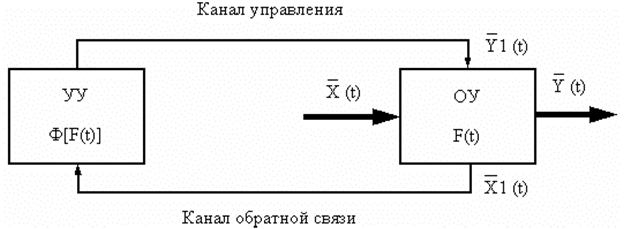
По определению, САУ охватывает объект управления (ОУ) и управляющего устройства (УУ). Системообразующие свойства САУ — информационные, среди которых объект управления со своими технологическими свойствами отображается производственной функцией F(t). Назначение САУ — управлять производственной функцией F(t), функция САУ Ф(t) — это функционал от F(t) — Ф[F(t)]. Таким образом, применение САУ позволяет понизить сложность функционала технологической системы до уровня функции системы управления (рис. 28).
Отличие от АСУ в этом примере заключается в следующем: объект-носитель — это ОУ и УУ; системообразующие свойства — это информационные свойства не только УУ, но и ОУ; в базе системы обычно отсутствует организационное обеспечение (персонал); все отношения в САУ, как правило, могут быть отображены в аналоговой форме. "Безлюдность" САУ позволяет использовать для ее анализа высокоразвитые и эффективные формальные методы ТАУ.
Обозначения: X(t), Y(t) — входной и выходной вектор технологических процессов объекта управления; X1(t), Y1(t) — входной и выходной вектор информационных процессов системы управления.
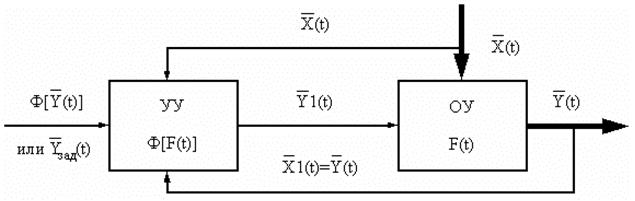
Управление осуществляется на основании контроля выходного и входного векторов функции ОУ по заранее заданному заданию (или по другому закону):
![\black\text{Ф}[\overline{Y}(t)]=\overline{Y}_{\text{зад}}(t)](/sites/default/files/tex_cache/7dce0c25105642d81132fef51b7da442.png) (см. рис. 29).
(см. рис. 29).
Внешняя среда здесь учитывается векторами 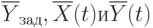 , а также факторами, учтенными при синтезе САУ.
, а также факторами, учтенными при синтезе САУ.
Вектор управления  определяется разницей векторов
определяется разницей векторов 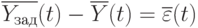
, где  — вектор рассогласования, и вектором возмущений X(t):
— вектор рассогласования, и вектором возмущений X(t):
![\black\overline{Y1}(t)=A_{\text{зад}}[\overline{\varepsilon}}(t)]-A_{\text{возм}}[\overline{X}(t)]](/sites/default/files/tex_cache/a5f8dfad3330070bfe19fee33854d51b.png) (1).
(1).
Определяются типовые элементы (звенья) САУ: безынерционные, инерционные, интегрирующие, дифференцирующие, запаздывающие и др. Состав САУ рассматривается как набор типовых звеньев.
![\black \text{Ф}[F(t)]\vdots((\overline{Y_{\text{зад}}}(t)\pm\overline{X1}(t)\pm\overline{X}(t))\rightarrow \overline{Y}(t))](/sites/default/files/tex_cache/4dd24521d4d1adf890d999e0758dec72.png)
Если САУ удовлетворяет условиям динамической системы, то ее функция преобразования одного входного сигнала x(t) в один выходной y(t) может иметь в общем случае форму обыкновенного дифференциального уравнения:
Ф[y(t), y'(t), ..., y(n)(t); x(t), x'(t), ..., x(n)(t), t]=0 (2),
или в упрощенном случае в форме линейного дифференциального уравнения вида:
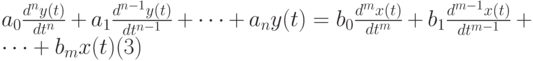
где ai, bi — коэффициенты уравнения.
Преобразованием Лапласа заменяют дифференциальное уравнение (3) на алгебраическое:
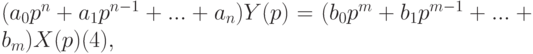
или D(p)Y(p)=K(p)X(p), где D(p) — собственный оператор, K(p) — входной оператор. Тогда функцию САУ, равную y(t)/x(t) можно заменить на передаточную функцию:
W(p)=Y(p)/X(p)=K(p)/D(p) (5).
Функция (5) и функциональная структура (4) САУ стационарны. Их устойчивость определяется дополнительными методами теории устойчивости, в результате чего на систему накладываются дополнительные условия.
Таким образом, прежде чем начать анализ функционирования САУ, мы вынуждены были провести ее общий системный анализ в соответствии с общим алгоритмом и теорией автоматического управления. При этом на САУ наложен ряд ограничений: 1) замена взаимных внешних отношений системы на однонаправленные входные и выходные сигналы; 2) выделение в САУ объекта управления и управляющего устройства: 3) использование заданной извне уставки функционала по отношению к управляемой величине; 4) ограничение внешних возмущающих воздействий; 5) линейность внешних (задающего и возмущающего) воздействий; 6) разделение САУ по типам на беспоисковые, поисковые, экстремальные, адаптивные; 7) направленность передачи воздействий; 8) применимость обыкновенных дифференциальных уравнений; 9) сосредоточенность параметров; 10) разбиение системы на цепи элементов однонаправленного преобразования входного сигнала в выходной; 11) применимость линейных дифференциальных уравнений; 12) применимость преобразований Лапласа.
III этап. Функционирование САУ.
В простейшем случае функционирование САУ описывается выражением
Y(p)=W(p)X(p) (6).
Однако, даже это простое выражение теория не рассматривает в общем случае, путем решения уравнений (4) и (3), а сводит задачу к рассмотрению совокупности типовых X(p) и W(p).
Типовые воздействия на САУ во времени t:
а) единичное ступенчатое воздействие
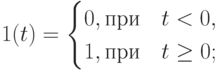
б) единичное импульсное воздействие или дельта-функция
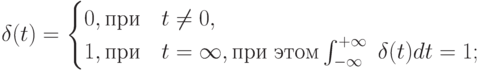
в) гармоническое воздействие
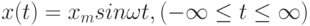
где xm — амплитуда сигнала, 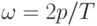 — круговая частота, рад/с, T — период сигнала, с;
— круговая частота, рад/с, T — период сигнала, с;
г) линейное воздействие

Все четыре типовых воздействия носят регулярный (детерминированный) характер, т. е. описываются математической функцией во времени. Однако, сигналы могут быть и нерегулярными (случайными), тогда для их описания используются средства математической статистики.
Любая САУ может находится в статическом режиме, когда y(t)=const, и в динамическом режиме, когда y(t)=var. Динамический режим может быть неустановившимся (переходным), сразу после изменения характера x(t), и установившимся, когда y(t) изменяется по тому же закону, что и x(t).
Обычно входные воздействия сводятся к типовым, в частности, к гармоническим, путем разложения любой периодической функции с периодом T
x(t)=x(t+iT), (i=0, 1, 2, ...),
удовлетворяющей условиям Дирихле (конечное число разрывов на интервале периода T), в бесконечный сходящийся тригонометрический ряд Фурье
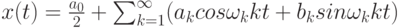
где 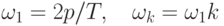 — круговые частоты, соответственно, основной и k-ой гармоник, рад/с; а0, аk, bk — независимые от t коэффициенты Фурье.
— круговые частоты, соответственно, основной и k-ой гармоник, рад/с; а0, аk, bk — независимые от t коэффициенты Фурье.
Непериодический сигнал может быть в предельном переходе 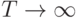 заменен интегралом Фурье.
заменен интегралом Фурье.
IY этап. Отображение САУ в системном пространстве.
В системном пространстве САУ отображается, прежде всего, передаточной функцией W(p), применение которой облегчается использованием математического аппарата, описывающего x(t) и y(t). Передаточная функция системы формируется по определенным правилам из передаточных функций отдельных звеньев. Для удобства, параллельно с W(p), вводится еще ряд типовых временных и частотных характеристик САУ:
а) передаточная характеристика h(t), как изменение выходной величины y(t) во времени, возникающее после подачи на вход единичного ступенчатого воздействия, при нулевых начальных условиях;
б) импульсная переходная характеристика 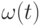 , как изменение выходной величины y(t), возникающее после подачи на вход
, как изменение выходной величины y(t), возникающее после подачи на вход 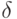 -функции, при нулевых начальных условиях;
-функции, при нулевых начальных условиях;
в) амплитудно-частотная характеристика  , как зависимость отношения амплитуд выходного и входного сигналов от частоты;
, как зависимость отношения амплитуд выходного и входного сигналов от частоты;
г) фазо-частотная характеристика 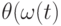 , как зависимость фазового сдвига между входным и выходным сигналами от частоты;
, как зависимость фазового сдвига между входным и выходным сигналами от частоты;
д) амплитудно-фазо-частотная характеристика 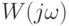 , модуль которой равен
, модуль которой равен  , а аргумент —
, а аргумент — 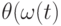 .
.
Таким образом, анализ функционирования САУ сводится к описанию x(t) в типовых формах, к описанию САУ передаточной функцией и типовыми характеристиками и к вычислению y(t) по выражению (6) и другим типовым зависимостям.
* ПРИМЕР 2. Анализ финансово-хозяйственной деятельности государственного предприятия [10, 72, 176].
Определим финансово-хозяйственную деятельность предприятия как производственный процесс, направленный на производство товарной продукции. Носитель системы — предприятие. Системообразующие свойства: 1) технологические, направленные на производство потребительской стоимости; 2) финансовые, позволяющие оценивать производимую потребительскую стоимость. Производственная система — это совокупность технологических и финансовых свойств предприятия, реализующих (в форме производственного процесса) функцию по производству товарной продукции. База системы: основные фонды предприятия, трудовые ресурсы, оборотные средства, система управления. Внешняя среда: покупатели, поставщики, финансовая система государства, руководящее министерство, прочие (рис. 30).
Уточним границы производственной системы: множество покупателей, формирующих цену спроса и потребляющих продукцию; множество поставщиков, формирующих цену предложения и поставляющих сырье; множество аналогичных систем, формирующих уровень рентабельности; государственная финансовая система, охватывающая как рыночные отношения (спроса, предложения, рентабельности), так и государственные регуляторы (эмиссия денег, золотой запас, учетная ставка, процент банковского кредита, антимонопольные законы, льготы, государственные программы, государственный сектор, государственный бюджет, законы по труду, пенсионному обеспечению и т. д.); руководящее министерство.
С учетом уточнения можно отметить, что в современных условиях ни в одном государстве ни одна производственная система не может производить стоимость по условиям "чистого рынка": спрос — предложение — рентабельность. Однако, в условиях централизованного управления всей экономикой (уровнем рентабельности) и обществом (спросом и предложением) понятие производственной системы предприятия теряет смысл. Сильным приближением является отнесение системы к экономике в целом и достаточно точным является отнесение системы к совокупности экономика — общество. Из приведенного уточнения понятий, однако, не следует, что эффективней работает множество производственных систем, чем одна система экономика — общество, или наоборот. Оптимизация любой из этих систем — многокритериальная, многопараметрическая задача, имеющая свои экстремумы, локальные оптимумы и глобальный оптимум, но по заданному критерию. В системе "экономика — общество СССР" выбранные критерии и их оптимизация оказались недостаточно эффективными и не оправдали основы самой системы.
II этап. Предпосылки анализа функционирования.
Проведенная на I этапе идентификация позволяет получить статическое описание производственной системы. Для описания ее функционирования необходимо все параметры системы представить в функции времени. Однако, теория микроэкономики требуемые временные зависимости заменяет набором их дискретных значений (планируемых и текущих). Планируемые значения могут фиксироваться на сутки, неделю, месяц, год и т. п., а текущая — как в плановые, так и в другие моменты времени.
При проведении анализа функционирования основными источниками информации служат стандартные формы отчетности: 1 — баланс; 2 — прибыли (доходы) и убытки; 3 — движение уставного (неделимого) фонда; 4 — недостача, хищения и порча товарно-материальных и других ценностей; 1-П — отчет о выполнении плана по продукции; 1-С — приложение к отчету о выполнении плана по себестоимости товарной продукции; 2-Т — отчет о выполнении плана по труду; 2-НТ — отчет о выполнении плана по основным показателям технического прогресса; 10-НТ — отчет о затратах на проведение научно-технических мероприятий и их экономической эффективности; 11 — наличие и движение основных средств (фондов) и амортизационного фонда; 13 — отчет о распределении прибыли; 22 — сводная таблица основных показателей, комплексно характеризующих хозяйственную деятельность предприятия; 24 — электробаланс, состав энергетического оборудования и отчет о работе электростанций (электрогенераторных установок); 31 — реализация промышленной продукции; формы квартальной отчетности.
III этап. Анализ функционирования.
Задача 3.1. Анализ производства и реализации продукции, в том числе:
- выполнения плана производства товарной продукции;
- выполнения плана по номенклатуре, ассортименту и структуре выпущенной продукции;
- качества продукции;
- реализации продукции;
- резервов увеличения выпусков и реализации товарной продукции.
Задача 3.2. Анализ труда и заработной платы, в том числе:
- численности работающих;
- использования рабочего времени;
- производительности труда;
- использования фонда заработной платы;
- резервов роста производительности труда и экономии фонда заработной платы.
Задача 3.3. Анализ основных промышленно-производственных фондов, в том числе:
- наличия и структуры основных фондов;
- состояния и движения основных фондов;
- вооруженности труда основными фондами;
- использования производственных основных фондов.
Задача 3.4. Анализ технического уровня производства, в том числе:
- коэффициента износа основных фондов;
- коэффициента обновления основных производственных фондов, в том числе их активной части;
- фондо- и технической вооруженности труда;
- обеспеченности средствами вычислительной техники;
- машиноемкости, трудоемкости и материалоемкости производства.
Задача 3.5. Анализ себестоимости продукции, в том числе:
- себестоимости товарной продукции;
- выполнения сметы затрат на производство;
- выполнения плана себестоимости товарной продукции по статьям калькуляции;
- затрат на рубль товарной продукции;
- себестоимости важнейших видов изделий;
- резервов снижения себестоимости продукции.
Задача 3.6. Анализ состояния и использования оборотных фондов, в том числе:
- обеспеченности предприятия собственными оборотными и приравненными к ним средствами;
- состояния оборотных средств;
- эффективности использования оборотных средств;
- общая оценка финансового состояния предприятия (сопоставление внеплановых активов по балансу с внеплановыми источниками средств);
- резервов улучшения использования оборотных средств.
Задача 3.7. Анализ прибыли и рентабельности, в том числе:
- балансовой прибыли;
- уровня общей рентабельности.
Рассмотренный пример анализа функционирования государственного предприятия, также как и пример синтеза частного предприятия, может решаться как экстремальная задача методами математического программирования (см. табл. 9, [2, 36, 53, 90, 196]).

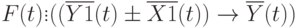 , а функционал
, а функционал