НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 2: Основы Maxima

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 556 / 141 | Длительность: 19:00:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

2.7.6 Преобразование рациональных выражений

Для выделения числителя и знаменателя дробных выражений используются функции num и denom :

(%i1)	expr:(x^2+1)/(x^3-1);

$\frac{{x}^{2}+1}{{x}^{3}-1}\leqno{(\%o1) }$

(%i2)	num(expr);

${x}^{2}+1\leqno{(\%o2) }$

(%i3)	denom(expr);

${x}^{3}-1\leqno{(\%o3) }$

Функция rat приводит выражение к каноническому представлению. Она упрощает любое выражение, рассматривая его как дробнорациональную функцию, т.е. работает с операциями "+", "-", "*", "/" и с возведением в целую степень.

Синтаксис вызова:

Переменные упорядочиваются в соответствии со списком 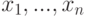x_1,... ,x_n . При этом вид ответа зависит от способа упорядочивания переменных Изначально переменные упорядочены в алфавитном порядке.

Пример использования rat :

(%i1)	((x - 2*y)^4/(x^2 - 4*y^2)^2 + 1)*(y + a)*(2*y + x) / (4*y^2 + x^2);

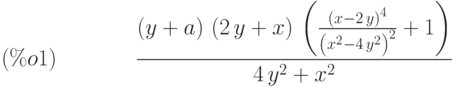
$\frac{\left( y+a\right) \,\left( 2\,y+x\right) \,\left( \frac{{\left( x-2\,y\right) }^{4}}{{\left( {x}^{2}-4\,{y}^{2}\right) }^{2}}+1\right) }{4\,{y}^{2}+{x}^{2}}\leqno{(\%o1) }$

(%i2)	rat(%);

$\frac{2\,y+2\,a}{2\,y+x}\leqno{(\%o2) }$

После указания порядка использования переменных получаем следующее выражение:

(%i3)	rat(%o1,y,a,x);

$\frac{2\,a+2\,y}{x+2\,y}\leqno{(\%o3) }$

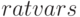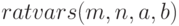Функция ratvars позволяет изменить алфавитный порядок предпочтения переменных, принятый по умолчанию. Вызов ratvars(z, y, x, w, v, u, t, s, r, q, p, o, n, m, l, k, j, i, h, g, f, e, d, c, b, a) меняет порядок предпочтения в точности на обратный, а вызов ratvars(m, n,a,b) упорядочивает переменные 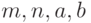m,n,a,b в порядке возрастания приоритета.

Флаг 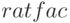ratfac включает или выключает частичную факторизацию выражений при сведении их к стандартной форме (CRE). Изначально установлено значение 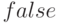false . Если установить значение 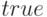true , то будет производиться частичная факторизация.

Функция ratsimp приводит все части (в том числе аргументы функций) выражения, которое не является дробно-рациональной функцией, к каноническому представлению, производя упрощения, которые не выполняет функция rat . Повторный вызов функции в общем случае может изменить результат, т.е. не обязательно упрощение проводится до конца. 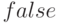Применением упрощения к экспоненциальным выражениям управляет флаг ratsimexpons , по умолчанию равный false , если его установить в 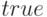true , упрощение применяется и к показателям степени или экспоненты.

(%i1)	sin (x/(x^2 + x)) = exp ((log(x) + 1)^2 - log(x)^2);

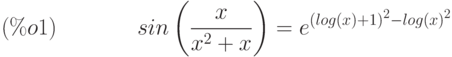
$sin\left( \frac{x}{{x}^{2}+x}\right) ={e}^{{\left( log\left( x\right) +1\right) }^{2}-{log\left( x\right) }^{2}}\leqno{(\%o1) }$

(%i2)	ratsimp(%);

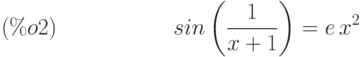
$sin\left( \frac{1}{x+1}\right) =e\,{x}^{2}\leqno{(\%o2) }$

(%i3)	((x - 1)^(3/2) - (x + 1)*sqrt(x - 1))/sqrt((x - 1)*(x + 1));

$\frac{{\left( x-1\right) }^{\frac{3}{2}}-\sqrt{x-1}\,\left( x+1\right) }{\sqrt{\left( x-1\right) \,\left( x+1\right) }}\leqno{(\%o3) }$

(%i4)	ratsimp(%);

$-\frac{2\,\sqrt{x-1}}{\sqrt{{x}^{2}-1}}\leqno{(\%o4) }$

(%i5)	x^(a + 1/a), ratsimpexpons: true;

${x}^{\frac{{a}^{2}+1}{a}}\leqno{(\%o5) }$

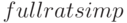Функция fullratsimp вызывает функцию ratsimp до тех пор, пока выражение не перестанет меняться.

Пример:

(%i1)	expr: (x^(a/2) + 1)^2*(x^(a/2) - 1)^2/(x^a - 1);

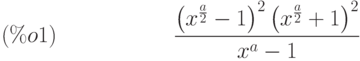
$\frac{{\left( {x}^{\frac{a}{2}}-1\right) }^{2}\,{\left( {x}^{\frac{a}{2}}+1\right) }^{2}}{{x}^{a}-1}\leqno{(\%o1) }$

(%i2)	ratsimp(expr);

$\frac{{x}^{2\,a}-2\,{x}^{a}+1}{{x}^{a}-1}\leqno{(\%o2) }$

(%i3)	fullratsimp(expr);

${x}^{a}-1\leqno{(\%o3) }$

(%i4)	rat(expr);

$\frac{{\left( {x}^{\frac{a}{2}}\right) }^{4}-2\,{\left( {x}^{\frac{a}{2}}\right) }^{2}+1}{{x}^{a}-1}\leqno{(\%o4) }$

Пример влияния флага ratsimpexponds на результат вычислений:

(%i1)	fullratsimp( exp((x^(a/2)-1)^2 *(x^(a/2)+1)^2 / (x^a-1) ) );

${e}^{\frac{{x}^{2\,a}}{{x}^{a}-1}-\frac{2\,{x}^{a}}{{x}^{a}-1}+\frac{1}{{x}^{a}-1}}\leqno{(\%o1) }$

(%i2)	ratsimpexpons:true;

$true\leqno{(\%o2) }$

(%i3)	fullratsimp( exp((x^(a/2)-1)^2 *(x^(a/2)+1)^2 / (x^a-1) ) );

${e}^{{x}^{a}-1}\leqno{(\%o3) }$

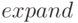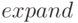Функция ratexpand раскрывает скобки в выражении. Отличается от функции expand тем, что приводит выражение к канонической форме, поэтому ответ может отличаться от результата применения функции expand :

(%i1)	ratexpand ((2*x - 3*y)^3);

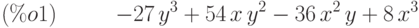
$-27\,{y}^{3}+54\,x\,{y}^{2}-36\,{x}^{2}\,y+8\,{x}^{3}\leqno{(\%o1) }$

(%i2)	expr: (x - 1)/(x + 1)^2 + 1/(x - 1);

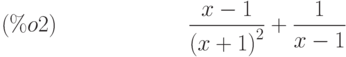
$\frac{x-1}{{\left( x+1\right) }^{2}}+\frac{1}{x-1}\leqno{(\%o2) }$

(%i3)	expand(expr);

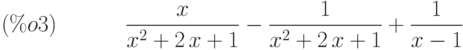
$\frac{x}{{x}^{2}+2\,x+1}-\frac{1}{{x}^{2}+2\,x+1}+\frac{1}{x-1}\leqno{(\%o3) }$

(%i4)	ratexpand(expr);

$\frac{2\,{x}^{2}}{{x}^{3}+{x}^{2}-x-1}+\frac{2}{{x}^{3}+{x}^{2}-x-1}\leqno{(\%o4) }$

Подстановка в рациональных выражениях осуществляется функцией ratsubst . Синтаксис вызова: ratsubst(a,b,c) Выражение подставляется вместо выражения в выражении ( может быть суммой, произведением, степенью и т.п.).

Пример использования ratsubst :

(%i1)	ratsubst (a, x*y^2, x^4*y^3 + x^4*y^8);

$a\,{x}^{3}\,y+{a}^{4}\leqno{(\%o1) }$

(%i2)	cos(x)^4 + cos(x)^3 + cos(x)^2 + cos(x) + 1;

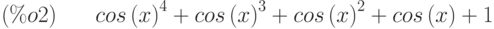
${cos\left( x\right) }^{4}+{cos\left( x\right) }^{3}+{cos\left( x\right) }^{2}+cos\left( x\right) +1\leqno{(\%o2) }$

(%i3)	ratsubst (1 –- sin(x)^2, cos(x)^2, %);

${sin\left( x\right) }^{4}-3\,{sin\left( x\right) }^{2}+cos\left( x\right) \,\left( 2-{sin\left( x\right) }^{2}\right) +3\leqno{(\%o3) }$

Дальше >>

Авторизоваться

Компьютерная математика с Maxima

Основы Maxima

2.7.6 Преобразование рациональных выражений

Вопросы и ответы