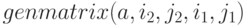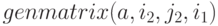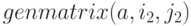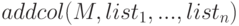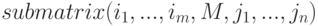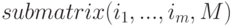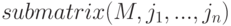Основы Maxima
2.7.2 Массивы
Массивы в Maxima — совокупности однотипных объектов с индексами. Число индексов не должно превышать пяти. В Maxima существуют и функции с индексами (функции массива).
Возможно создание и использование переменных с индексами до объявления соответствующего массива. Такие переменные рассматриваются как элементы массивов с неопределёнными размерностями (так называемые хэш-массивы). Размеры неопределённых массивов растут динамически по мере присваивания значений элементам. Интересно, что индексы массивов с неопределёнными границами не обязательно должны быть числами. Для повышения эффективности вычислений рекомендуется преобразовывать массивы с неопределёнными границами в обычные массивы (для этого используется функция  ).
).
Создание массива производится функцией array. Синтаксис обращения к функции:  — создание массива с именем name и размерностями
— создание массива с именем name и размерностями 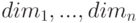 ; array(name,type,dim_1,... ,dim_n) — создание массива с именем name и элементами типа
; array(name,type,dim_1,... ,dim_n) — создание массива с именем name и элементами типа 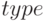 ;
; ![array([name_1,... ,name_m],dim_1,... ,dim_n)](/sites/default/files/tex_cache/a4742edccd55e6babc00fa7ea74f648c.png) — создание нескольких массивов одинаковой размерноcти.
— создание нескольких массивов одинаковой размерноcти.
Индексы обычного массива — целые числа, изменяющиеся от 0 до
 .
.
Пример:
(%i1) array(a,1,1);

(%i2) a[0,0]:0; a[0,1]:1; a[1,0]:2; a[1,1]:3;

(%i6) listarray(a);
![[0,1,2,3]\leqno{(\%o6) }](/sites/default/files/tex_cache/8c9b7ecf060eac982e5f6113d175a192.png)
Функция 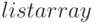 , использованная в примере, преобразует массив в список. Синтаксис вызова:
, использованная в примере, преобразует массив в список. Синтаксис вызова: 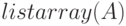 .
.
Аргумент  может быть определённым или неопределённым массивом, функцией массива или функцией с индексами. Порядок включения элементов массива в список — по строкам.
может быть определённым или неопределённым массивом, функцией массива или функцией с индексами. Порядок включения элементов массива в список — по строкам.
Функция 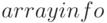 выводит информацию о массиве
выводит информацию о массиве  . Синтаксис вызова:
. Синтаксис вызова: 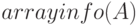 Аргумент
Аргумент  , как и в случае
, как и в случае 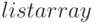 , может быть определённым или неопределённым массивом, функцией массива или функцией с индексами.
, может быть определённым или неопределённым массивом, функцией массива или функцией с индексами.
Пример использования:
(%i1) array (aa, 2, 3);

(%i2) aa [2, 3] : %pi;

(%i3) aa [1, 2] : %e;

(%i4) arrayinfo (aa);
![[declared,2,[2,3]]\leqno{(\%o4) }](/sites/default/files/tex_cache/51d87e1a6e4b02403fe10656c4a614e2.png)
(%i5) bb [FOO] : (a + b)^2;

(%i6) bb [BAR] : (c - d)^3;

(%i7) arrayinfo (bb);
![[hashed,1,[BAR],[FOO]]\leqno{(\%o7) }](/sites/default/files/tex_cache/c4845d223235091174d405ac4c3d053c.png)
(%i8) listarray (bb);
![[{\left( c-d\right) }^{3},{\left( b+a\right) }^{2}]\leqno{(\%o8) }](/sites/default/files/tex_cache/10826d7159586dd87971ab1135af4a86.png)
Функции 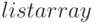 и
и 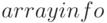 применимы и к функциям массива:
применимы и к функциям массива:
(%i9) cc [x, y] := y / x;

(%i10) cc[1,2];

(%i11) cc[2,1];

(%i12) arrayinfo(cc);
![[hashed,2,[1,2],[2,1]]\leqno{(\%o12) }](/sites/default/files/tex_cache/c39652e9d89d876a1a7eef2ab8fdafdf.png)
(%i13) listarray(cc);
![[2,\frac{1}{2}]\leqno{(\%o13) }](/sites/default/files/tex_cache/2dc913a2c3eb2b506dbbfe95af00563a.png)
Ещё один пример — создание и вывод информации о функциях с индексами:
(%i1) dd [x] (y) := y ^ x;

(%i2) dd[1](4);

(%i3) dd[a+b];
![lambda\left( [y],{y}^{b+a}\right) \leqno{(\%o3) }](/sites/default/files/tex_cache/5876f1c4ecccf02783019f05d6477495.png)
(%i4) arrayinfo(dd);
![[hashed,1,[1],[b+a]]\leqno{(\%o4) }](/sites/default/files/tex_cache/85fdcab68d98136137e6b5e2c7c881ce.png)
(%i5) listarray(dd);
![[lambda\left( [y],y\right) ,lambda\left( [y],{y}^{b+a}\right) ]\leqno{(\%o5) }](/sites/default/files/tex_cache/97140a9d67d43114bbeac3094b03d593.png)
Функция 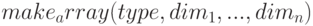 создаёт и возвращает массив Lisp. Тип массива может быть
создаёт и возвращает массив Lisp. Тип массива может быть 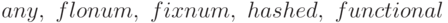 . Индекс
. Индекс  может изменяться в пределах от 0 до
может изменяться в пределах от 0 до 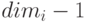 .
.
Достоинство 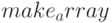 по сравнению с
по сравнению с  — возможность динамически управлять распределением памяти для массивов. Присваивание
— возможность динамически управлять распределением памяти для массивов. Присваивание 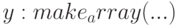 создаёт ссылку на массив. Когда массив больше не нужен, ссылка уничтожается присваиванием
создаёт ссылку на массив. Когда массив больше не нужен, ссылка уничтожается присваиванием  , память освобождается затем сборщиком мусора.
, память освобождается затем сборщиком мусора.
Примеры:
(%i1) A1 : make_array (fixnum, 8);
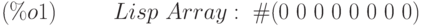
(%i2) A1[1]:8;

(%i3) A3 : make_array (any, 8);
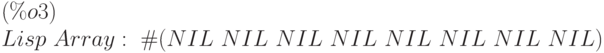
(%i4) arrayinfo(A3);
![[declared,1,[7]]\leqno{(\%o4) }](/sites/default/files/tex_cache/4f892d6f473af67602ba2d327bae83d9.png)
Переменная  содержит список имён массивов первого и второго видов, определённых на данный момент.
содержит список имён массивов первого и второго видов, определённых на данный момент.
Пример:
(%i1) array(a,1,1);

(%i2) array(b,2,3);

(%i3) arrays;
![[a,b]\leqno{(\%o3) }](/sites/default/files/tex_cache/23b2986d9f61adb60094e95442bb64ef.png)
Функция 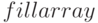 позволяет заполнять массивы значениями из другого массива или списка. Заполнения производится по строкам.
позволяет заполнять массивы значениями из другого массива или списка. Заполнения производится по строкам.
Примеры:
(%i1) array(a,1,1);

(%i2) fillarray(a,[1,2,3,4]);

(%i3) a[1,1];

(%i4) a2 : make_array (fixnum, 8);
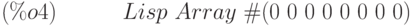
(%i5) fillarray (a2, [1, 2, 3, 4, 5]);
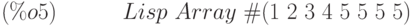
Как видно из рассмотренных примеров, длина списка может и не совпадать с размерностью массива. Если указан тип массива, он должен заполняться элементами того же типа. Удаление массивов из памяти осуществляется функцией 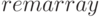 .
.
Кроме того, для изменения размерности массива имеется функция 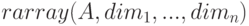 . Новый массив заполняется элементами старого по строкам. Если размер старого массива меньше, чем нового, остаток нового заполняется нулями или
. Новый массив заполняется элементами старого по строкам. Если размер старого массива меньше, чем нового, остаток нового заполняется нулями или 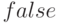 (в зависимости от типа массива).
(в зависимости от типа массива).
2.7.3 Матрицы и простейшие операции с ними
В Maxima определены прямоугольные матрицы.
Основной способ создания матриц — использования функции matrix. Синтаксис вызова: 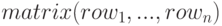 . Каждая строка — список выражений, все строки одинаковой длины. На множестве матриц определены операции сложения, вычитания, умножения и деления. Эти операции выполняются поэлементно, если операнды — две матрицы, скаляр и матрица или матрица и скаляр. Возведение в степень возможно, если один из операндов — скаляр. Перемножение матриц (в общем случае некоммутативная операция) обозначается символом ". ". Операция умножения матрицы самой на себя может рассматриваться как возведение в степень. Возведение в степень -1 — как обращение (если это возможно).
. Каждая строка — список выражений, все строки одинаковой длины. На множестве матриц определены операции сложения, вычитания, умножения и деления. Эти операции выполняются поэлементно, если операнды — две матрицы, скаляр и матрица или матрица и скаляр. Возведение в степень возможно, если один из операндов — скаляр. Перемножение матриц (в общем случае некоммутативная операция) обозначается символом ". ". Операция умножения матрицы самой на себя может рассматриваться как возведение в степень. Возведение в степень -1 — как обращение (если это возможно).
Пример создания двух матриц:
(%i1) x: matrix ([17, 3], [-8, 11]);
![\leqno{(\%o1)}\left[\begin{array}{ll}
17 & 3 \\
-8 & 11
\end{array}\right]](/sites/default/files/tex_cache/453fc957de964d475ff4709a84ade470.png)
(%i2) y: matrix ([%pi, %e], [a, b]);
![\leqno{(\%o2)}\left[\begin{array}{ll}
\pi & e \\
a & b
\end{array}\right]](/sites/default/files/tex_cache/1649af0d119e99fe585050634d20c9d9.png)
Выполнение арифметических операций с матрицами:
(%i3) x+y;
![\leqno{(\%o3)}\left[\begin{array}{ll}
\pi +17 & e+3\\
a-8 & b+11
\end{array}\right]](/sites/default/files/tex_cache/e4aefdd45657faa8d22df1cbea126cda.png)
(%i4) x-y;
![\leqno{(\%o4)}\left[\begin{array}{ll}
17 -\pi & 3-e \\
-a-8 & 11-b
\end{array}\right]](/sites/default/files/tex_cache/2e01cc61c27a2717858322b7bba7bf4e.png)
(%i5) x*y;
![\leqno{(\%o5)}\left[\begin{array}{ll}
17 \,\pi & 3 \,e \\
-a\,8 & 11\,b
\end{array}\right]](/sites/default/files/tex_cache/282e0037f94824b0b28c2d856c4b9e79.png)
(%i6) x/y;
![\leqno{(\%o6)}\left[\begin{array}{ll}
\frac{17}{\pi } & 3\,{e}^{-1} \\
-\frac{8}{a} & \frac{11}{b}
\end{array}\right]](/sites/default/files/tex_cache/aca271948e49cb02b2446befc888bfac.png)
Обратите внимание — операции выполняются поэлементно. При попытке выполнять арифметические операции, как представлено выше, над матрицами различных размеров, выдаётся ошибка.
Пример операций с матрицами и скалярами:
(%i9) x^3;
![\leqno{(\%o9)}\left[\begin{array}{ll}
4913 & 27 \\
-512 & 1331
\end{array}\right]](/sites/default/files/tex_cache/e7ee0a3af5b1828f9df9acc3baec3162.png)
(%i10) 3^x;
![\leqno{(\%o10)}\left[\begin{array}{ll}
129140163 & 27 \\
\frac{1}{6561} & 177147
\end{array}\right]](/sites/default/files/tex_cache/002f2af1dec919cc1714322407c41456.png)
Умножение матрицы на матрицу:
(%i11) x.y;
![\leqno{(\%o11)}\left[\begin{array}{ll}
3\,a+17\,\pi & 3\,b+17\,e \\
11\,a-8\,\pi & 11\,b-8\,e
\end{array}\right]](/sites/default/files/tex_cache/267c6bf3d78b54bb20195dd03565d595.png)
(%i12) y.x;
![\leqno{(\%o12)}\left[\begin{array}{ll}
17\,\pi -8\,e & 3\,\pi +11\,e \\
17\,a-8\,b & 11\,b+3\,a
\end{array}\right]](/sites/default/files/tex_cache/2bda8502cb873f437986cf39a1af868e.png)
Очевидно, что для успешного перемножения матрицы должны быть согласованы по размерам. Возведение в степень -1 даёт обратную матрицу:
(%i13) x^^-1;
![\leqno{(\%o13)}\left[\begin{array}{ll}
\frac{11}{211} & -\frac{3}{211} \\
\frac{8}{211} & \frac{17}{211}
\end{array}\right]](/sites/default/files/tex_cache/c9595ef7dd16fcd24ee5b3afd50e90e8.png)
(%i14) x.(x^^-1);
![\leqno{(\%o14)}\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]](/sites/default/files/tex_cache/18c6d80276f8a9cff0b42660ccaa364c.png)
Стоит обратить внимание, что операции x^^-1 и x^-1 дают разный результат!
Пример:
(%i2) x^-1;
![\leqno{(\%o2)}\left[\begin{array}{ll}
\frac{1}{17} & \frac{1}{3}\\
-\frac{1}{8} & \frac{1}{11}
\end{array}\right]](/sites/default/files/tex_cache/35c0d99ea2aa6c28573fc8efd9db7d50.png)
(%i3) x^^-1;
![\leqno{(\%o3)}\left[\begin{array}{ll}
\frac{11}{211} & -\frac{3}{211}\\
\frac{8}{211}& \frac{17}{211}
\end{array}\right]](/sites/default/files/tex_cache/e47eb2512cae09e9a758b1100ce08d97.png)
Функция  возвращает матрицу заданной размерности, составленную из элементов двухиндексного массива. Синтаксис вызова:
возвращает матрицу заданной размерности, составленную из элементов двухиндексного массива. Синтаксис вызова:
Индексы 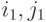 и
и 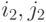 указывают левый и правый нижний элементы матрицы в исходном массиве.
указывают левый и правый нижний элементы матрицы в исходном массиве.
Пример:
(%i1) h [i, j] := 1 / (i + j - 1);
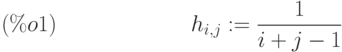
(%i2) genmatrix(h,3,3);
![\leqno{(\%o2)}\left[\begin{array}{lll}
1 & \frac{1}{2} & \frac{1}{3}\\
\frac{1}{2} & \frac{1}{3} & \frac{1}{4}\\
\frac{1}{3} & \frac{1}{4} & \frac{1}{5}
\end{array}\right]](/sites/default/files/tex_cache/4473b89cc0dc4ffb161d787f72c946fb.png)
(%i3) array (a, fixnum, 2, 2);

(%i4) a [1, 1] : %e;

(%i5) a [2, 2] : %pi;

(%i6) genmatrix (a, 2, 2);
![\leqno{(\%o6)}\left[\begin{array}{ll}
e & 0\\
0 & \pi
\end{array}\right]](/sites/default/files/tex_cache/16038d9bc91540655b82dd18b5e73fae.png)
Функция  возвращает матрицу заданной размерности, составленную из нулей (синтаксис вызова
возвращает матрицу заданной размерности, составленную из нулей (синтаксис вызова 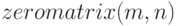 ).
).
(%i7) zeromatrix(2,2);
![\leqno{(\%o7)}\left[\begin{array}{ll}
0 & 0\\
0 & 0
\end{array}\right]](/sites/default/files/tex_cache/58a1c02962711372fc71aedd544a4840.png)
Функция  возвращает единичную матрицу заданной размерности (синтаксис
возвращает единичную матрицу заданной размерности (синтаксис 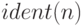 )
)
(%i9) ident(2);
![\leqno{(\%o9)}\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]](/sites/default/files/tex_cache/db5b5f42c64e2b2c550a27ea3cd5e716.png)
Функция  создаёт копию матрицы
создаёт копию матрицы  . Обратите внимание, что присваивание не создаёт копии матрицы (как и присваивание не создаёт копии списка).
. Обратите внимание, что присваивание не создаёт копии матрицы (как и присваивание не создаёт копии списка).
Пример:
(%i1) a:matrix([1,2],[3,4]);
![\leqno{(\%o1)}\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]](/sites/default/files/tex_cache/afb19ff5afd8684c67bfa40f186876fb.png)
(%i2) b:a;
![\leqno{(\%o2)}\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]](/sites/default/files/tex_cache/521dedef1345f6353998ede5c6d5a6ab.png)
(%i3) b[2,2]:10;

(%i4) a;
![\leqno{(\%o4)}\left[\begin{array}{ll}
1 & 2 \\
3 & 10
\end{array}\right]](/sites/default/files/tex_cache/576094914c3d6c31a1b732d872c96185.png)
Присваивание нового значения элементу матрицы  изменяет и значение соответствующего элемента матрицы
изменяет и значение соответствующего элемента матрицы  . Использование
. Использование  позволяет избежать этого эффекта.
позволяет избежать этого эффекта.
Функции 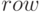 и
и 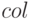 позволят извлечь соответственно строку и столбец заданной матрицы, получая список. Синтаксис вызова:
позволят извлечь соответственно строку и столбец заданной матрицы, получая список. Синтаксис вызова:
-
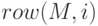 — возвращает
— возвращает  -ю строку;
-ю строку; -
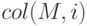 — возвращает
— возвращает  -й столбец.
-й столбец.
Функции 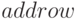 и
и 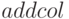 добавляют к матрице строку или столбец соответственно. Синтаксис вызова:
добавляют к матрице строку или столбец соответственно. Синтаксис вызова:
Здесь 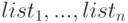 — добавляемые строки или столбцы.
— добавляемые строки или столбцы.
Пример:
(%i1) a:matrix([1,2],[3,4]);
![\leqno{(\%o1)}\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]](/sites/default/files/tex_cache/afb19ff5afd8684c67bfa40f186876fb.png)
(%i2) b:addrow(a,[10,20]);
![\leqno{(\%o2)}\left[\begin{array}{ll}
1 & 2\\
3 & 4\\
10 & 20
\end{array}\right]](/sites/default/files/tex_cache/7b2f7dcf36823b6e0fd8cb012a2274b0.png)
(%i3) addcol(b,[x,y,z]);
![\leqno{(\%o3)}\left[\begin{array}{lll}
1 & 2 & x\\
3 & 4 & y\\
10 & 20 & z
\end{array}\right]](/sites/default/files/tex_cache/9ba6b49811229909be4281bbfe19e4ff.png)
Функция 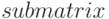 возвращает новую матрицу, состоящую из подматрицы заданной. Синтаксис вызова:
возвращает новую матрицу, состоящую из подматрицы заданной. Синтаксис вызова:
Подматрица строится следующим образом: из матрицы  удаляются строки
удаляются строки 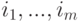 и
и 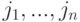 .
.
Пример (используем последний результат из предыдущего примера, удаляем третью строку и третий столбец):
(%i6) submatrix(3,%,3);
![\leqno{(\%o6)}\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]](/sites/default/files/tex_cache/2f5fd909fda634720aaf892602fc96cb.png)
Для заполнения матрицы значениями некоторой функции используется функция 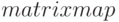 (аналог
(аналог 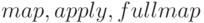 ). Синтаксис вызова: matrixmap(f,M). Функция matrixmap возвращает матрицу с элементами
). Синтаксис вызова: matrixmap(f,M). Функция matrixmap возвращает матрицу с элементами 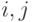 , равными
, равными ![f(M[i,j])](/sites/default/files/tex_cache/919292b3a890ae9e02fd1afdcdd56fec.png) .
.
Пример:
(%i1) a:matrix([1,2],[3,4]);
![\leqno{(\%o1)}\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]](/sites/default/files/tex_cache/afb19ff5afd8684c67bfa40f186876fb.png)
(%i2) f(x):=x^2;

(%i3) matrixmap(f,a);
![\leqno{(\%o3)}\left[\begin{array}{ll}
1 & 4 \\
9 & 16
\end{array}\right]](/sites/default/files/tex_cache/42522fdc92459cdd5dba1101f294ecfd.png)
Для работы с матрицами существует ещё много функций, но они относятся к решению различных задач линейной алгебры, поэтому обсуждаются ниже, в главе 3.2.