НОУ ИНТУИТ | Программирование на языке С++ в среде Qt Creator. Лекция 5: Массивы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 07.03.2015 | Доступ: свободный | Студентов: 2136 / 487 | Длительность: 24:14:00

Тема: Программирование

Специальности: Программист, Архитектор программного обеспечения

|

Вам нравится? Нравится 74 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

5.5 Указатели на функции

При решении некоторых задач возникает необходимость передавать имя функции как параметр. В этом случае формальным параметром является указатель на передаваемую функцию. В общем виде прототип указателя на функцию можно записать так.

type (*name_f ) ( type1, type2, type3,...)

Здесь

name_f — имя функции
type — тип, возвращаемый функцией,
type1, type2, type3,... — типы формальных параметров функции.

В качестве примера рассмотрим решение широко известной математической задачи.

Задача 5.13. Вычислить 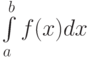$\int\limits_a^b f(x)dx$ методами Гаусса и Чебышёва.

Кратко напомним читателю методы численного интегрирования.

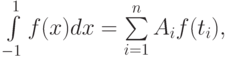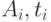Метод Гаусса состоит в следующем. Определённый интеграл непрерывной функции на интервале от -1 до 1 можно заменить суммой и вычислить по формуле $\int\limits_{-1}^1 f(x)dx=\sum\limits_{i=1}^n A_if(t_i),\t_i$ — точки из интервала [-1, 1], A_i — рассчитываемые коэффициенты. Методика определения A_i, t_i представлена в [3]. Для практического использования значения коэффициентов при 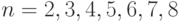n = 2, 3, 4, 5, 6, 7, 8 представлены в табл. 5.5.

Таблица 5.5. : Значения коэффициентов в квадратурной формуле Гаусса
n	Массив t	Массив A
2	-0.57735027, 0.57735027	1,1
3	-0.77459667, 0, 0.77459667	5/9, 8/9, 5/9
4	-0.86113631, -0.33998104, 0.33998104,0.86113631	0.34785484, 0.65214516, 0.65214516, 0.34785484
5	-0.90617985, -0.53846931, 0, 0.53846931,0.90617985	0.23692688, 0.47862868, 0.568888889,0.47862868, 0.23692688
6	-0.93246951, -0.66120939, -0.23861919, 0.23861919, 0.66120939, 0.93246951	0.17132450, 0.36076158, 0.46791394, 0.46791394, 0.36076158, 0.17132450
7	-0.94910791, -0.74153119, -0.40584515, 0, 0.40584515, 0.74153119, 0.94910791	0.12948496, 0.27970540, 0.38183006, 0.41795918, 0.38183006, 0.27970540, 0.12948496
8	-0.96028986, -0.79666648, -0.52553242, -0.18343464, 0.18343464, 0.52553242, 0.79666648, 0.96028986	0.10122854, 0.22238104, 0.31370664, 0.36268378, 0.36268378, 0.31370664, 0.22238104, 0.10122854

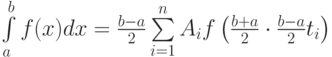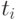Для вычисления интеграла непрерывной функции на интервале от до квадратурная формула Гаусса может быть записана следующим образом $\int\limits_a^bf(x)dx=\frac{b-a}{2}\sum\limits_{i=1}^nA_if\left(\frac{b+a}{2}\cdot {\frac{b-a}{2}}t_i\right)$ , значения коэффициентов A_i и t_i приведены в табл. 5.5

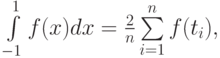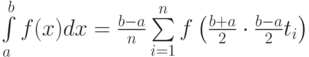При использовании квадратурной формулы Чебышёва, определённый интеграл непрерывной функции на интервале от -1 до 1 записывается в виде следующей формулы $\int\limits_{-1}^1f(x)dx=\frac{2}{n}\sum\limits_{i=1}^nf(t_{i}),\t_{i}$ — точки из интервала [-1, 1]. Формула Чебышёва для вычисления интеграла на интервале от до может быть записана так $\int\limits_{a}^{b}f(x)dx=\frac{b-a}{n}\sum\limits_{i=1}^{n}f\left(\frac{b+a}{2}\cdot {\frac{b-a}{2}}t_{i}\right)$ Методика определения 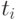t_i представлена в [3]. Рассмотренные формулы имеют смысл при 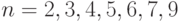n = 2, 3, 4, 5, 6, 7, 9 , коэффициенты 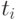t_i представлены в табл. 5.6.

Таблица 5.6. Значения коэффициентов в квадратурной формуле Чебышёва
n	Массив t
2	-0.577350, 0.577350
3	-0.707107, 0, -0.707107
4	-0.794654, -0.187592, 0.187592, 0.794654
5	-0.832498, -0.374541, 0, 0.374541, 0.832498
6	-0.866247, -0.422519, -0.266635, 0.266635, 0.422519, 0.866247
7	-0.883862, -0.529657, -0.323912, 0, 0.323912, 0.529657, 0.883862
9	-0.911589, -0.601019, -0.528762, -0.167906, 0, 0.167906, 0.528762, 0.601019, 0.911589

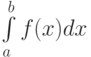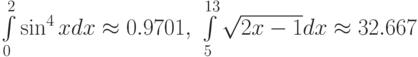Осталось написать функции вычисления определённого интеграла $\int\limits_{a}^{b}f(x)dx$ методами Гаусса и Чебышёва. Далее приведены тексты функций и функция main(). В качестве тестовых использовались интегралы $\int\limits_{0}^{2}\sin ^{4}xdx\approx 0.9701,\ \int\limits_{5}^{13}\sqrt{2x-1}dx\approx 32.667$ .

#include <iostream>
#include <math.h>
using namespace std;
//Функция вычисления определённого интеграла методом Чебышёва.
//(a, b) — интервал интегрирования, *fn — указатель на функцию типа double f (double).
double int_chebishev ( double a, double b,
double (*fn ) ( double ) )
{
	int i, n=9;
	double s,
	t [ 9 ]= {-0.911589, -0.601019, -0.528762, -0.167906, 0, 0.167906, 0.528762,
		0.601019, 0.911589 };
	for ( s= i =0; i<n; i++)
		s+=fn ( ( b+a ) /2+(b-a ) /2*t [ i ] );
	s *=(b-a ) /n;
	return s;
}
//Функция вычисления определённого интеграла методом Гаусса.
//(a, b) — интервал интегрирования, *fn — указатель на функцию типа double f (double)
double int_gauss ( double a, double b, double (*fn ) ( double ) )
{
	int i, n=8;
	double s,
	t [8]= { -0.96028986, -0.79666648, -0.52553242, -0.18343464, 0.18343464,
		0.52553242, 0.79666648, 0.96028986 },
	A[8]= { 0.10122854, 0.22238104, 0.31370664, 0.36268378, 0.36268378,
		0.31370664, 0.22238104, 0.10122854 };
	for ( s= i =0; i<n; i++)
		s+=A [ i ] *fn ( ( b+a ) /2+(b-a ) /2* t [ i ] );
	s *=(b-a ) / 2;
	reurn s;
}
//Функции f1 и f2 типа double f(double), указатели на которые будут передаваться
//в int_gauss и int_chebishev.
double f1 ( double y )
{
	return sin(y) *sin(y) *sin(y) *sin( );
}
double f2 ( double y )
{
	return pow ( 2*y -1, 0.5 );
}
int main ( int argc, char **argv )
{
	double a, b;
	cout<<"Интеграл sin(x)^4 = \n ";
	cout<<"Введите интервал интегрирования\n ";
	cin>>a>>b;
	//Вызов функции int_gauss(a, b, f1), f1 — имя функции, интеграл от которой надо посчитать.
	cout<<"Метод Гаусса:"<<int_gauss ( a, b, f1 )<<endl;
	//Вызов функции int_chebishev(a, b, f1),
	//f1 — имя функции, интеграл от которой надо посчитать.
	cout<<"Метод Чебышёва:"<<int_chebishev( a, b, f1 )<<endl;
	cout<<"Интеграл sqrt ( 2*x-1 ) =\n ";
	cout<<"Введите интервалы интегрирования\n ";
	cin>>a>>b;
	//Вызов функции int_gauss(a, b, f2), f2 — имя функции, интеграл от которой надо посчитать.
	cout<<"Метод Гаусса:"<<int_gauss ( a, b, f2 )<<endl;
	//Вызов функции int_chebishev(a, b, f2),
	//f2 — имя функции, интеграл от которой надо посчитать.
	cout<<"Метод Чебышёва:"<<int_chebishev ( a, b, f2 )<<endl;
	return 0;
}

Результаты работы программы приведены ниже

Интеграл sin(x)^4=
Введите интервалы интегрирования
0 2
Метод Гаусса:0.970118
Метод Чебышёва:0.970082
Интеграл sqrt(2*x-1)=
Введите интервалы интегрирования
5 13
Метод Гаусса:32.6667
Метод Чебышёва:32.6667

Дальше >>

Авторизоваться

Программирование на языке С++ в среде Qt Creator

Массивы

5.5 Указатели на функции

Вопросы и ответы