|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Массивы
Задача 5.9. Удалить из массива все отрицательные элементы, расположенные между максимальным и минимальным элементами массива X[n].
Решение этой задачи можно разделить на следующие этапы:
- Ввод массива.
- Поиск номеров максимального (nmax) и минимального (nmin) элементов массива.
- Определение меньшего (a) и большего (b) из чисел nmax и nmin.
- Далее, необходимо перебрать все элементы массива, расположенные между числами с номерами a и b. Если число окажется отрицательным, то его необходимо удалить. Однако на этом этапе нужно учитывать тонкий момент. Если просто организовать цикл от a+1 до b-1, то при удалении элемента изменяется количество элементов, расположенных между a и b, и номер последнего удаляемого элемента. Это может привести к тому, что не всегда корректно будут удаляться отрицательные элементы, расположенные между a и b. Поэтому этот цикл для удаления организован несколько иначе.
Текст программы:
#include <iostream>
#include <math.h>
using namespace std;
int main ( int argc, char **argv )
{
int i, j, k, n, nmax, nmin, *x, a, b;
cout<<" n = "; cin>>n; //Ввод количества элементов в массиве.
x=new int [ n ]; //Выделяем память для динамического массива x.
cout<<"Введите элементы массива X \n "; //Ввод элементов массива.
for ( i =0; i<n; i++)
cin>>x [ i ];
//Поиск номеров максимального и минимального элементов в массиве.
for (nmax=nmin= i =0; i<n; i++)
{
if ( x [ i ]<x [ nmin ] ) nmin= i;
if ( x [ i ]>x [ nmax ] ) nmax= i;
}
//Проверяем, что раньше расположено, минимум или максимум
if ( nmin<nmax )
{
a=nmin;
b=nmax;
}
else
{
a=nmax;
b=nmin;
}
//Перебираем все элементы, расположенные между максимумом и минимумом
for ( i=a+1,k=1;k<=b-a-1;k++)
if ( x [ i ] <0) //Проверяем, является ли очередной элемент массива отрицательным.
{//Если текущий элемент массива является отрицательным числом, удаляем его
for ( j= i; j<n-1; j++)
x [ j ]=x [ j + 1 ];
n--;
}
else i ++; //Если x[i]>=0, переходим к следующему элементу.
cout<<"Преобразованный массив X\n ";
for ( i =0; i<n; i++)
cout<<x [ i ]<<" \t ";
cout<<endl;
return 0;
}
В качестве тестового можно использовать следующий массив: 34, 4, -7, -8, -10, 7, -100, -200, -300, 1. Здесь приведённая выше программа работает корректно, а вариант
for ( i=a+1; i<b; )
if ( x [ i ] <0)
{
for ( j= i; j<n-1; j++)
x [ j ]=x [ j + 1 ];
n--;
}
else i ++;
приводит к неправильным результатам. Рекомендуем читателю самостоятельно разобраться в особенностях подобных алгоритмов удаления.
Задача 5.10. В массиве X[n] найти группу наибольшей длины, которая состоит из знакочередующихся чисел.
Если будут вычислены следующие значения:
- nach — номер первого элемента в группе;
- kon — номер последнего элемента в группе;
- k — количество элементов в группе.
то, зная любые два из них, можно однозначно определить группу внутри массива.
Вначале количество элементов в знакочередующейся группе равно 1. Дело в том, что если мы встретим первую пару знакочередующихся элементов, то количество их в группе сразу станет равным 2. Однако все последующие пары элементов будут увеличивать k на 1. И чтобы не решать проблему построения последовательности значений k 0,2,3,4,5,..., первоначальное значение k примем равным 1. Когда будем встречать очередную пару подряд идущих соседних элементов, то k необходимо будет увеличить на 1.
Алгоритм поиска очередной группы состоит в следующем: попарно (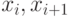 ) перебираем все элементы массива (параметр цикла
) перебираем все элементы массива (параметр цикла  изменяется от 0 до n - 2).
изменяется от 0 до n - 2).
Если произведение соседних элементов отрицательно ( ), то это означает, что они имеют разные знаки и являются элементами группы. В этом случае количество (
), то это означает, что они имеют разные знаки и являются элементами группы. В этом случае количество ( ) элементов в группе увеличиваем на 1 (k++). Если же произведение соседних элементов положительно (
) элементов в группе увеличиваем на 1 (k++). Если же произведение соседних элементов положительно (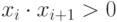 ), то эти элементы не являются членами группы. В этом случае возможны два варианта:
), то эти элементы не являются членами группы. В этом случае возможны два варианта:
- Если
 , то только что закончилась группа, в этом случае kon=i -номер последнего элемента в группе,
, то только что закончилась группа, в этом случае kon=i -номер последнего элемента в группе,  — количество элементов в только что закончившейся группе.
— количество элементов в только что закончившейся группе. - Если
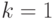 , то это просто очередная пара незнакочередующихся элементов.
, то это просто очередная пара незнакочередующихся элементов.
После того, как закончилась очередная группа знакочередующихся элементов, необходимо количество групп (kgr) увеличить на 1 (kgr++). Если это первая группа (kgr=1) знакочередующихся элементов, то в переменную max записываем длину этой группы (max=k)3В переменной, а в переменную kon_max номер последнего элемента группы (kon_max=i). Если это не первая группа (kgr=1), то сравниваем max и длину текущей группы (k). Если k>max, то в переменную max записываем длину этой группы (max=k), а в переменную kon_max номер последнего элемента группы (kon_max=i).
После этого в переменную k опять записываем 1 для формирования новой группы элементов.
По окончанию цикла значение k может быть больше 1. Это означает, что в самом конце массива встретилась ещё одна группа. Для неё надо будет провести все те же действия, что и для любой другой группы. Далее приведён текст программы.
#include <iostream>
using namespace std;
int main ( int argc, char **argv )
{ float *x;
int i, k, n, max, kgr, kon_max;
cout<<" n = "; cin>>n; //Ввод размера массива.
x=new float [ n ]; //Выделение памяти для массива.
cout<<"Введите массив x\n "; //Ввод элементов массива.
for ( i =0; i<n; i++)
cin>>x [ i ];
//Попарно перебираем элементы массива. Количество знакочередующихся
//групп в массиве kgr=0, количество элементов в текущей группе — 1.
for ( kgr= i =0,k=1; i<n-1; i++)
//Если соседние элементы имеют разные знаки, то количество (k)
//элементов в группе увеличиваем на 1.
if ( x [ i ] * x [ i +1]<0) k++;
else
if ( k>1) //Если k>1, то только что закончилась группа, i — номер последнего элемента
{//в группе, k — количество элементов в группе. Увеличиваем kgr на 1.
kgr++;
if ( kgr==1) //Если это первая группа (kgr=1) знакочередующихся элементов,
{
max=k; //то max — длина группы (max=k),
kon_max= i; //kon_max — номер последнего элемента группы.
}
else //это не первая группа (kgr 6= 1), сравниваем max и длину текущей группы.
if ( k>max) //Если k>max,
{
max=k; //max — длина группы,
kon_max= i; //kon_max — номер последнего элемента группы.
}
k=1; //В переменную k записываем 1 для формирования новой группы элементов.
}
if ( k>1) //Если в конце массива была группа.
{
kgr++; //Количество групп увеличиваем на 1.
if ( kgr==1) //Если это первая группа,
{
max=k; //то max — длина группы,
kon_max=n-1; //группа закончилась на последнем элементе массива.
}
else
if ( k>max) //Если длина очередной группы больше max.
{
max=k; //то в max записываем длину последней группы,
kon_max=n-1; //группа закончилась на последнем элементе массива.
}
}
if ( kgr >0) //Если знакочередующиеся группы были,
{ //то выводим информацию о группе наибольшей длины,
cout<<"В массиве "<<kgr<<" групп знакочередующихся элементов\n ";
cout<<"Группа максимальной длины начинается с элемента Номер
"<<kon_max-max+1<<", её длина "<<max<<",номер последнего элемента группы
" <<kon_max<<endl;
for ( i=kon_max-max+1; i<=kon_max; i++) //а также саму группу.
cout<<x [ i ]<<" ";
cout<<endl;
}
else //Если знакочередующихся групп не было, то выводим сообщение об этом.
cout<<"В массиве нет групп знакочередующихся элементов\n ";
return 0;
}
