Операторы управления

Задача 3.4. Написать программу решения квадратного уравнения .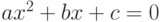

Исходные данные: вещественные числа 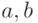и — коэффициенты квадратного уравнения.

Результаты работы программы: вещественные числа 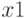и — корни квадратного уравнения либо сообщение о том, что корней нет.

Вспомогательные переменные: вещественная переменная , в которой будет храниться дискриминант квадратного уравнения.

Составим словесный алгоритм решения этой задачи.

1. Начало алгоритма.
2. Ввод числовых значений переменных 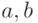и .
3. Вычисление значения дискриминанта по формуле .
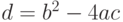4. Если 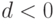, то переход к п.5, иначе переход к п.6.
5. Вывод сообщения "Действительных корней нет" и переход к п.8.
6. Вычисление корней 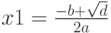и .
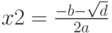7. Вывод значени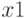й и на экран.
8. Конец алгоритма.

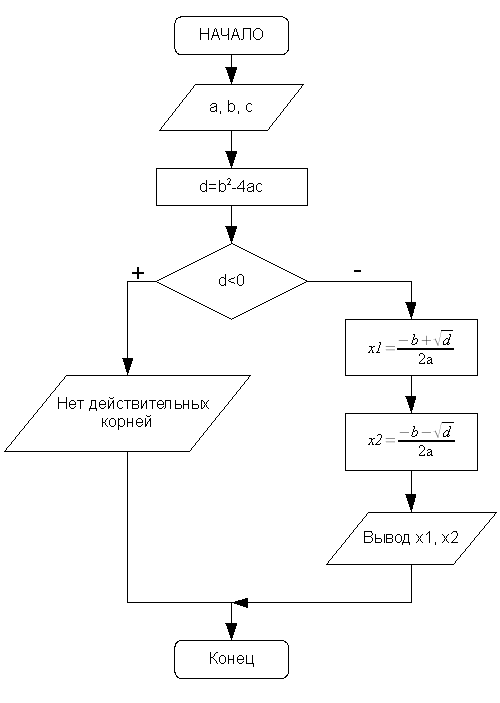
Блок-схема, соответствующая этому описанию, представлена на рис. 3.15.

Текст программы, которая реализует решение квадратного уравнения:

#include <iostream>
#include <math.h>
using namespace std;
int main ( )
{
	float a, b, c, d, x1, x2;
	//Ввод значений коэффициентов квадратного уравнения.
	cout<<" a = "; cin >>a;
	cout<<" b = "; cin >>b;
	cout<<" c = "; cin >>c;
	d=b*b-4*a*c; //Вычисление дискриминанта.
	if (d<0)
		//Если дискриминант отрицательный, то вывод сообщения, о том что действительных корней нет,
		cout<<"Нет действительных корней";
	else
	{
		//иначе вычисление действительных корней
		x1=( -b+sqrt (d) ) /2/a;
		x2=( -b-sqrt (d) ) /(2 * a);
		//и вывод их значений.
		cout<<" X1 = "<<x1<<" \t X2 = "<<x2<<" \n ";
	}
	return 0;
}
			

Рис. 3.15. Алгоритм решения квадратного уравнения

Задача 3.5. Составить программу нахождения действительных и комплексных корней квадратного уравнения .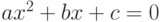

Исходные данные: вещественные числа a, b и c — коэффициенты квадратного уравнения.

Результаты работы программы: вещественные числа 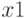и — действительные корни квадратного уравнения либо 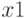и — действительная и мнимая части комплексных корней квадратного уравнения.

Вспомогательные переменные: вещественная переменная , в которой будет храниться дискриминант квадратного уравнения.

Можно выделить следующие этапы решения задачи:

1. Ввод коэффициентов квадратного уравнения 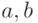и .
2. Вычисление дискриминанта по формуле .
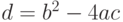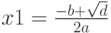3. Проверка знака дискриминанта. Если , то вычисление действительных корней: и 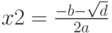и вывод их на экран. При отрицательном дискриминанте выводится сообщение о том, что действительных корней нет, и вычисляются комплексные корни^{2Комплексные числа записываются в ви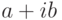де , где — действительная часть комплекс-ного числа, — мнимая часть комплексного числа, — мнимая единица 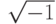. Подробно о комплексных числах можно прочитать в главе 9.} .

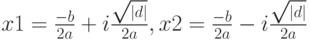У обоих комплексных корней действительные части одинаковые, а мнимые отличаются знаком. Поэтому можно в переменной 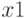хранить действительную часть числа 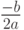, в переменной — модуль мнимой части 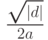, а в качестве корней вывест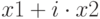и и .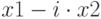

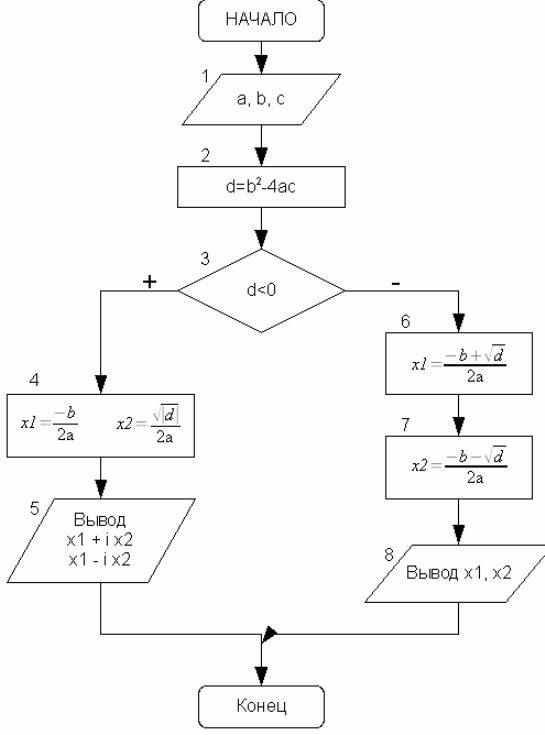
На рис. 3.16 изображена блок-схема решения задачи. Блок 1 предназначен для ввода коэффициентов квадратного уравнения. В блоке 2 осуществляется вычисление дискриминанта. Блок 3 осуществляет проверку знака дискриминанта, если дискриминант отрицателен, то корни комплексные, их расчёт происходит в блоке 4 (действительная часть корня записывается в переменную 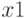, модуль мнимой — в переменную ), а вывод — в блоке 5 (первый корень 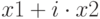, второй — 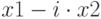). Если дискриминант положителен, то вычисляются действительные корни уравнения (блок 6) и выводятся на экран (блок 7).

Текст программы, реализующей поставленную задачу:

#include <iostream>
#include <math.h>
using namespace std;
int main ( )
{
	float a, b, c, d, x1, x2;
	cout<<" a = "; cin>>a;
	cout<<" b = "; cin>>b;
	cout<<" c = "; cin>>c;
	d=b*b-4*a*c;
	if (d<0)
	{ //Если дискриминант отрицательный, то вывод соответствующего сообщения.
		cout<<"Нет вещественных корней \n ";
		x1=-b/(2 * a ); //Вычисление действительной части комплексных корней.
		x2=sqrt ( fabs (d) ) /(2 * a ); //Вычисление модуля мнимой части комплексных корней
		//Сообщение о комплексных корнях уравнения вида ax2 + bx + c = 0.
		cout<<"Комплексные корни уравнения \n ";
		cout<<a<<" x ^2+ "<<b<<" x + "<<c<<" =0 \n ";
		//Вывод значений комплексных корней в виде x1 + ix2, x1 - ix2 
		if ( x2>=0)
		{
			cout<<x1<<" + "<<x2<<" i \t ";
			cout<<x1<<" -"<<x2<<" i \n ";
		}
		else
		{
			cout<<x1<<" -"<<abs ( x2 )<<" i \t ";
			cout<<x1<<" + "<<abs ( x2 )<<" i \n ";
		}
	}
	else
	{
		//Если дискриминант положительный, вычисление действительных корней и вывод их на экран.
		x1=( -b+sqrt (d) ) /2/a;
		x2=( -b- sqrt (d) ) /(2 * a );
		cout<<"Вещественные корни уравнения \n ";
		cout<<a<<" x ^2+ "<<b<<" x + "<<c<<" =0 \n ";
		cout<< X1 = "<<x1<<" \t X2 = "<<x2<<" \n ";
	}
	return 0;
}
			

Рис. 3.16. Алгоритм решения задачи 3.5

Результаты работы программы к задаче 3.5 показаны ниже.

a=-5
b=-3
c=-4
Нет вещественных корней
Комплексные корни уравнения
-5x^2+-3x+-4=0
-0.3-0.842615i -0.3+0.842615i
==============================
a=2
b=-3
c=1
Вещественные корни уравнения
2x^2+-3x+1=0
X1=1 X2=0.5