Объектно-ориентированное программирование в C#
Дополнительные материалы к занятию можно скачать ![]() здесь.
здесь.
Упражнение 7.1. Создание простого класса
Создаем новое консольное приложение C#. Называем проект practice_3_1.
Наберите в окне кода следующую программу:
using System;
class goods
{
public string ProductName;
public DateTime ExpireDate;
public double Price;
}
class Example
{
static void Main()
{
goods Product = new goods();
Product.ProductName = "Хлеб Изобилие";
Product.ExpireDate = new DateTime(2011, 5, 1, 8, 30, 52);
Product.Price = 43.54;
string str;
str = "Товар: " + Product.ProductName + "\nСрок годности: " + Product.ExpireDate + "\nЦена: " + Product.Price + " рубля";
Console.WriteLine(str);
Console.WriteLine("Нажмите любую кнопку!");
Console.ReadKey();
}
}
Получаем следующий результат:
Упражнение 7.2. Создание двух экземпляров одного класса
Создаем новое консольное приложение C#. Называем проект practice_3_2.
Наберите в окне кода следующую программу:
using System;
class goods
{
public string ProductName;
public DateTime ExpireDate;
public double Price;
}
class Example
{
static void Main()
{
goods Bread = new goods();
Bread.ProductName = "Хлеб Изобилие";
Bread.ExpireDate = new DateTime(2011, 5, 1, 8, 30, 52);
Bread.Price = 43.54;
goods Milk = new goods();
Milk.ProductName = "Молоко";
Milk.ExpireDate = new DateTime(2011, 5, 5, 6, 30, 52);
Milk.Price = 35.6;
string str;
str = "Товар: " + Bread.ProductName + "\nСрок годности: " + Bread.ExpireDate + "\nЦена: " + Bread.Price + " рубля";
str += "\nТовар: " + Milk.ProductName + "\nСрок годности: " + Milk.ExpireDate + "\nЦена: " + Milk.Price + " рубля";
Console.WriteLine(str);
Console.WriteLine("Нажмите любую кнопку!");
Console.ReadKey();
}
}
Получаем следующий результат:
Упражнение 7.3. Знакомство с методами класса
Создаем новое консольное приложение C#. Называем проект practice_3_3.
Наберите в окне кода следующую программу:
using System;
class shape
{
public double Length(double r)
{
double l;
l = 2 * Math.PI * r;
return l;
}
public double Area(double r)
{
double s;
s = Math.PI * Math.Pow(r, 2);
return s;
}
}
class Example
{
static void Main()
{
shape figure = new shape();
double a;
a = 10;
double l, s;
l = figure.Length(a);
s = figure.Area(a);
string str;
str = "Радиус равен " + a;
str += "\nДлина окружности равна " + l;
str += "\nПлощадь круга равна " + s;
Console.WriteLine(str);
Console.WriteLine("Нажмите любую кнопку!");
Console.ReadKey();
}
}
Листинг
.
Получаем следующий результат:
Упражнение 7.4. Знакомство с методами класса (продолжение)
Создаем новое консольное приложение C#. Называем проект practice_3_4.
Наберите в окне кода следующую программу:
using System;
class shape
{
public double r;
public double SphereArea()
{
double s;
s = 4 * Math.PI * Math.Pow(r, 2);
return s;
}
public double SphereVolume()
{
double v;
v = 4 * Math.PI * Math.Pow(r, 3) / 3;
return v;
}
}
class Example
{
static void Main()
{
shape figure = new shape();
double a;
a = 10;
figure.r = a;
double v, s;
s = figure.SphereArea();
v = figure.SphereVolume();
string str;
str = "Радиус равен " + a;
str += "\nПлощадь сферы равна " + s;
str += "\nОбъем шара равен " + v;
Console.WriteLine(str);
Console.WriteLine("Нажмите любую кнопку!");
Console.ReadKey();
}
}
Листинг
.
Получаем следующий результат:
Упражнение 7.5. Нахождение широты, долготы и высоты спутника ГЛОНАСС исходя из его геоцентрических координат
Даны следующие геоцентрические координаты спутника:


Геоцентрические координаты связаны с широтой и долготой следующими соотношениями:

Найдем радиус-вектор  , соединяющий объект с центром масс Земли:
, соединяющий объект с центром масс Земли:

Широта 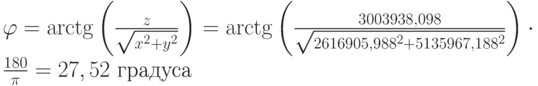
Долгота 
Для нахождения высоты над уровнем моря  мы вычтем радиус Земли
мы вычтем радиус Земли 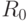 из радиус-вектора
из радиус-вектора  :
:
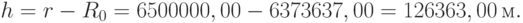
Создаем новое консольное приложение C#. Называем проект practice_3_5.
Наберите в окне кода следующую программу:
using System;
class Satellite
{
public double x;
public double y;
public double z;
double R0 = 6373637.00; //Радиус Земли
public double Height()
{
double h;
h = Math.Sqrt(Math.Pow(x, 2) + Math.Pow(y, 2) + Math.Pow(z, 2)) - R0;
return h;
}
public double Latitude()
{
double phi;
phi = Math.Atan(z / Math.Sqrt(Math.Pow(x, 2) + Math.Pow(y, 2))) * 180 / Math.PI;
return phi;
}
public double Longitude()
{
double lambda;
lambda = Math.Atan(y / x) * 180 / Math.PI;
return lambda;
}
}
class Example
{
static void Main()
{
double x, y, z;
x = 2616905.988;
y = 5135967.188;
z = 3003938.098;
Satellite GLONASS = new Satellite();
GLONASS.x = x;
GLONASS.y = y;
GLONASS.z = z;
double h, phi, lambda;
h = GLONASS.Height();
phi = GLONASS.Latitude();
lambda = GLONASS.Longitude();
string str;
str = "Высота над уровнем моря: " + h + " метра" + "\nГеографическая широта: " + phi + " градуса"
+ "\nГеографическая долгота " + lambda + " градуса";
Console.WriteLine(str);
Console.WriteLine("Нажмите любую кнопку!");
Console.ReadKey();
}
}
Листинг
.
Получаем следующий результат:
Задание: Преобразование декартовых координат {x,y,z} в геодезические {H,L,B}
Связь между геодезическими параметрами 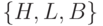 точки пространства и декартовыми координатами
точки пространства и декартовыми координатами 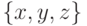 можно определить следующим образом:
можно определить следующим образом:
![x=(N+H)\cos B\cos L,\;y=(N+H)\cos B\sin L,\;z=[(1-e^2)N+H]\sin B,](/sites/default/files/tex_cache/61184509f7bd135101a3117c278ccc7a.png)
где:
-
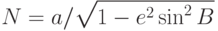 - радиус кривизны в точке местной вертикали
- радиус кривизны в точке местной вертикали  ,
, -
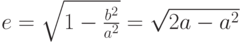 эксцентриситет эллипсоида,
эксцентриситет эллипсоида, -
 - параметр сжатия эллипсоида.
- параметр сжатия эллипсоида.
Для преобразования координат мы воспользуемся алгоритмом, описанном в ГОСТ Р 51794-2001 (…Методы преобразований координат определяемых точек), внеся в него небольшие изменения.
Алгоритм предполагает следующую последовательность действий:
- Вычислить вспомогательную величину
 по формуле
по формуле 
- Проанализировать значение
 следующим образом:
следующим образом:
- а) если
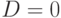 , то
, то 
- б) если
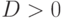 , то
, то 
при этом

- а) если
- Проанализировать значение
 :
:
- а) если
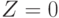 , то
, то 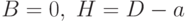
- б) во всех других случаях вычисления выполняют следующим образом:
Найти вспомогательную величину
 по следующей формуле:Геодезическая широта B находится следующим образом:
по следующей формуле:Геодезическая широта B находится следующим образом: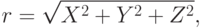

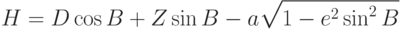
- а) если
Итак, мы имеем следующие исходные данные:

- Вычислим вспомогательную величину
 :
:
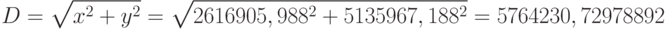
- Так, как
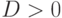 , то пункт 2a пропускаем. Переходим к пункту 2б.
Найдем геодезическую долготу
, то пункт 2a пропускаем. Переходим к пункту 2б.
Найдем геодезическую долготу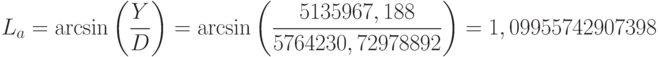
 :
:
Так как
Найдем значение геодезической долготы в градусах: и
и  , то
, то  .
.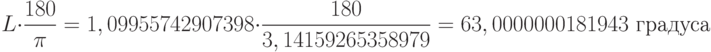
- Проанализируем значение
 . Так как
. Так как 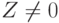 , то пункт 3а пропускаем и переходим к пункту 3б. Найдем вспомогательную величину
, то пункт 3а пропускаем и переходим к пункту 3б. Найдем вспомогательную величину  :
Найдем геодезическую широту
:
Найдем геодезическую широту
 :
Переведем радианы в градусы:
:
Переведем радианы в градусы: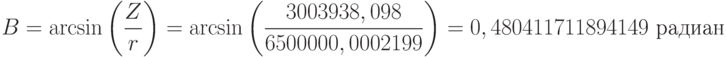 Найдем геодезическую высоту
Найдем геодезическую высоту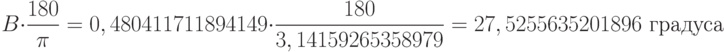
 :
:
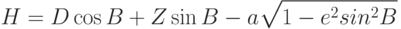
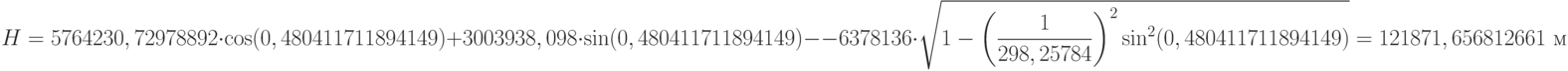
Разработать соответствующую программу