|
Уточните пожалуйста, какие документы для этого необходимо предоставить с моей стороны. Курс "Объектно-ориентированное программирование и программная инженения". |
Введение в лямбда исчисление
Лямбда-исчисление
Мы уже познакомились с основами агентов и даже некоторыми деталями. Надеюсь, вы ощутили мощь этого механизма и возможные области его применения.
Фактически возможен следующий уровень гибкости. Прежде чем его освоить, следует рассмотреть математические идеи, лежащие в основе. Лямбда-исчисление даст нам более глубокое понимание агентов, в частности, концепции открытых и закрытых операндов.
Эта замечательная теория разработана в 1930 году еще до появления компьютеров. Через 30 лет обнаружилось, что она дает ясную и прочную основу многих концепций языков программирования. Это оживило интерес к лямбда-исчислению, и оно стало плодотворной областью исследований.
Лямбда-исчисление дает нам теорию понятия функции. Оно занимается основами понятия, не изучая специальные виды функций, таких как функции тригонометрии или функции вещественных переменных. Здесь изучается сама идея функции как механизма, принимающего аргументы и вырабатывающего результат. Это математическое понятие, но оно весьма схоже с понятием программы в компьютерных науках. Теория позволяет нам лучше понять, что является областью определения переменной, какова роль аргументов, а также возможность рассматривать программу как объект, отвечая целям этой лекции — преобразовать программы в агенты.
Операции над функциями
Основная идея проста: нотация и правила трансформации позволяют нам обращаться с функциями так же, как и с другими математическим объектами.
Для заданных двух чисел a и b можно образовывать различные комбинации, например: a + b или sin(a) + cos(b), используя функции с хорошо определенной сигнатурой.
sin: REAL ? REAL - Смысл: Для любого аргумента типа REAL функция sin
- вырабатывает результат типа REAL
"+": [REAL х REAL] ? REAL
- х декартово произведение, квадратные скобки
- применяются для группировки аргументов
Можно ли "играть" в подобные игры не с числами, а с функциями? Даже в элементарной операции мы встречаемся с операциями над функциями. Если f и g — это функции с подходящими сигнатурами, то можно задать их композицию, записываемую как g o f или f ; g (нотация, которую мы будем использовать, поскольку она явно указывает порядок выполнения). Результатом композиции является функция h(x ), такая, что h(x) = g(f (x)) для любого применимого аргумента x. Композиция является такой же операцией над функциями, как "+" над числами.
Лямбда-исчисление позволит нам определить над функциями много операций.
Мы можем продолжить восхождение по лестнице абстракций. Композиция функций является функцией, поэтому и к ней применима композиция. Пусть X, Y, Z — некоторые множества и заданы сигнатуры функций f и g:
f: X ? Y g: Y ? Z
Композиция этих функций, названная выше функцией h, имеет сигнатуру X ? Z. Определим теперь композицию "; " как функцию, которой передаются два аргумента f и g и которая вырабатывает результат h. Эта функция имеет сигнатуру:
";":[[X ? Y ] х [Y ? Z ]] х [X ? Z]Листинг 6.1.
Мы можем продолжить определение функций, которые оперируют функциями, которые, в свою очередь, оперируют функциями, и так далее. Лямбда-исчисление дает нам словарь и правила — теорию — для работы с такими функциями на произвольном уровне.
Лямбда-выражения
Прежде всего, нам необходима простая нотация для определения функций. Будем предполагать, что у нас есть базис
из функций, таких как "+", над целыми и вещественными. Это предположение делается для простоты, так как
лямбда-исчисление может быть определено без ссылок на существующие математические теории. Символ
 будет, как обычно, означать "по определению". Определим функцию square с сигнатурой
будет, как обычно, означать "по определению". Определим функцию square с сигнатурой
square : REAL ? REAL
Функция в качестве результата возвращает квадрат числа. Ее определение можно задать соответствующим лямбда-выражением:
 |
( 6.2) |
Правая часть определения является лямбда-выражением, запись которого однозначно позволяет установить, что для любого x типа REAL результатом функции будет x * x.
Символ ? (лямбда) - дело соглашения, но он дал имя всему подходу. В математической литературе сигнатуру от определения функции отделяет символ точки, но в ОО-программировании точка играет другую важную роль, поэтому вместо точки применяется символ " | " вертикальной черты.
Лямбда-определение функции напоминает ее определение в программировании
square (x: REAL): REAL - x в квадрате. do Result := x * x endЛистинг 6.3.
Как правило, математическая нотация всегда компактнее программистской. В этой нотации переменная, следующая за ?, называется связанной переменной лямбда-выражения, она подобна формальному аргументу метода.
Подобно имени формального аргумента, имя связанной переменной не влияет на смысл выражения и может быть любым. Так что следующее определение задает ту же самую функцию, вычисляющую квадрат числа:
? y: REAL | y * y
Это наблюдение будет формализовано ниже, используя понятие альфа-преобразования. Лямбда-выражение может иметь более одной связанной переменной, требуется лишь, чтобы у них были разные имена:
? x, y: INTEGER | x + y — Функция сложения ? x: NATURAL, z : REAL | zx — Нотация для случая разных типов
Чем хорошо лямбда-выражение? На первый взгляд, вместо него можно было бы использовать уже знакомую запись, например, для функции square:
? x : REAL | square (x) = x * xЛистинг 6.4.
Разница в том, что [6.4] определяет свойства функции, в то время как [6.2] определяет функцию — математический объект со всеми правами, аналогично тому, как можно определить константу ?, задав ее значение.
Одним из непосредственных преимуществ является возможность определения функций высших порядков, таких как композиция, сигнатура которой задана в [6.1]:
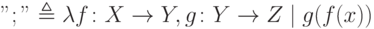
Предполагается, что множества X, Y, Z известны. Так как они произвольны, мы можем ввести механизм универсальности в лямбда-выражение, как для классов, превращая имена множеств в формальные родовые параметры. В нашем кратком обзоре нет необходимости в такой нотации.
В этом примере исходное множество в сигнатуре является декартовым произведением [X ? Y * [Y ? Z] ; соответственно, лямбда-выражение имеет две связанные переменные — f и g.
До сих пор каждому определению функции лямбда-выражением предшествовало задание сигнатуры функции, а каждая связанная переменная сопровождалась указанием ее типа. В принципе, возможно нетипизированное лямбда-выражение, но мы будем продолжать использовать только типизированные, аналогично тому, как мы используем в программировании типизированные языки, такие как Eiffel, повышая читабельность и избегая ошибок.
Почувствуй методологию
Объявление сигнатуры
Объявление сигнатуры функции должно предшествовать определению функции лямбда-выражением.
Если сигнатура появляется непосредственно перед определением, то в определении можно опускать связанные переменные, как в этом примере:
![";":[[X \to Y] * [Y \to Z]] * [X \to Z]
\\";" \triangleq \lambda f,g \colon g (f (x)) \text { - Нет необходимости в объявлении f и g}](/sites/default/files/tex_cache/fa543a13ca90720233ab0eb3879bc7df.png)
