|
Уточните пожалуйста, какие документы для этого необходимо предоставить с моей стороны. Курс "Объектно-ориентированное программирование и программная инженения". |
Введение в лямбда исчисление
Карринг
В качестве примера функции высшего порядка, которую можно описать лямбда-выражением, рассмотрим карринг.
Карринг назван в честь американского математика Карри Брукса Хаскелла — одного из основателей теории, известной как комбинаторная логика, частью которой является лямбда-исчисление. Карринг, без потери общности, позволяет рассматривать функции, имеющие только один аргумент. Вначале соглашение, связанное с нотацией:
Почувствуй нотацию
Квадратные и круглые скобки
В обычной математической нотации круглые скобки служат как для группирования, так и для записи функций. В примере f(a * (b + с)) внутренние скобки используются для группирования, внешние - для записи функции. Это приводило бы к непониманию при обсуждении операций над функциями. При обсуждении лямбда-исчисления круглые скобки будут применяться только при задании функции, а для группировки используются квадратные скобки. Так, запись:
[f ; g](a * [b + с])
означает применение композиции функций f и g к аргументу, заданному выражением - произведением a и суммы b+с.
Часто приходится иметь дело с бинарными функциями, имеющими два аргумента, такими как композиция ";" " или сложение "+". Рассмотрим такую функцию:
f : [ X х Y ] ? Z
для заданных X, Y, Z. Зная f, определим функцию f' с сигнатурой:
f' : X ? [ Y ? Z]
как
![f' \triangleq \lambda x \colon X [\lambda y \colon Y \mid f (x,y)]](/sites/default/files/tex_cache/545d39e5aeff387bc0deb57c96350e14.png) |
( 6.5) |
Что это означает? В отличие от f функция f' принимает только один аргумент типа X, а также в отличие от f не возвращает результат типа Z. Вместо этого она для любого x в качестве результата возвращает функцию, заданную в [2.22]. Давайте назовем эту функцию g. Эта функция от одного аргумента y типа Y возвращает результат типа Z. Результат g(x) — тот же, что и f(x, y), как если бы сразу применили пару аргументов к функции f.
Функцию f' называют карризованной версией функции f. Карринг двухаргументной функции означает преобразование ее в одноаргументную функцию, связанную с оригиналом соотношением [6.5]. Говорят также, что карринг означает специализацию функции по первому аргументу. Специализация, связывая первый аргумент, оставляет свободным только второй аргумент, что и преобразует функцию в одноаргументную.
Если функция add — сложение целых, определение которой можно задать лямбда-выражением
 , то curry(add) является функцией:
, то curry(add) является функцией:
![add' \triangleq \lambda x:INTEGER \mid [\lambda y : INTEGER | x + y]](/sites/default/files/tex_cache/9b53a1ddc7022e24972d31b236e113ad.png)
Так что add' (1) - ?y: INTEGER | 1 + y — это функция " плюс 1", добавляющая 1 к заданному числу.
Соответствие между двухаргументной функцией f и ее карризованной версией f' взаимно однозначно. Неформально при проведении карринга никакая информация не теряется, так как эффект второго аргумента остается встроенным в аргумент результирующей функции f'.
Будет интересно — и послужит примером выразительной силы лямбда-нотации — явно установить соответствие между f и f ', рассматривая карринг как функцию curry, определяемую лямбда-выражением. Для заданных X, Y, Z ее сигнатура:
curry: [[X х Y ] ? Z ] ? [X ? [Y ? Z ]]
Ее значение
![curry \triangleq \lambda f:[X х Y ] \to Z \mid [\lambda x : X \mid [\lambda y:Y \mid f(x,y)]]](/sites/default/files/tex_cache/91fa7ee1f78e92f50ee35e54319a7393.png)
Аналогично определите обратное соответствие, создающее f по функции f'.
Обобщение карринга
Во всех примерах карринг применялся к двухаргументной функции по первому аргументу. Достаточно просто обобщить концепцию: карринг можно применять к любой функции из n (n ? 1) аргументов для любого выбора m аргументов (1 ? m ? n), задав значения для выбранного набора аргументов. Это превращает исходную функцию в функцию с n - m аргументами, представляя специализированную версию исходной функции, также известной как частичное вычисление. Если m = n, то получаем константную функцию.
Карринг на практике
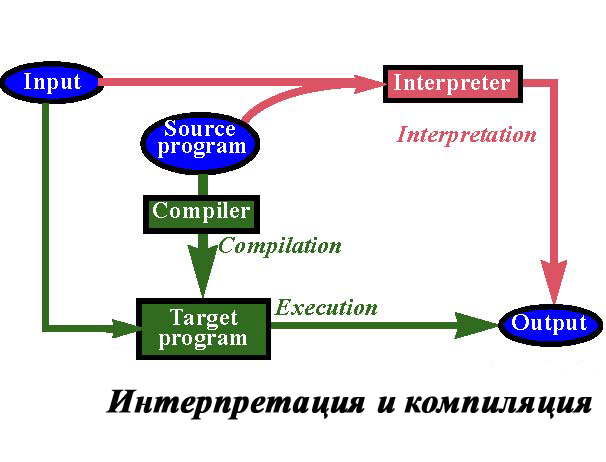
Как пример того, что карринг представляет на практике, рассмотрим разницу между компиляцией и интерпретацией.
Интерпретатор с абстрактной точки зрения можно рассматривать как функцию с сигнатурой:
interpreter : Program х Input ? Output
Здесь Program — множество всех корректных программ, Input и Output — множества возможных входов и выходов (это упрощенная, но достаточно корректная точка зрения на программы). Компилятор создает из исходной программы машинный код, который на компьютере уже без дополнительных усилий может быть выполнен на некотором входе:

Абстрактно работу компилятора можно рассматривать как функцию с сигнатурой:
compiler : Program ? [Input ? Output]
Когда у нас есть два механизма выполнения для одного и того же языка программирования, важно, чтобы они реализовали одну и ту же семантику.
Это основа работы в EiffelStudio, где постоянно приходится переключаться от полностью скомпилированной, полностью оптимизированной — финальной формы компиляции к быстрой возрастающей перекомпиляции — "технологии тающего льда", где главным образом применяется интерпретация. Конечно, при поставке конечного продукта выполняется финальная компиляция, но результаты работы совпадают с версией "тающего льда".
Требование согласованной работы компилятора и интерпретатора точно и элегантно выразимо с использованием карринга:
compiler = curry (interpreter)
ОО-стиль программирования отвечает духу карринга. ОО-вычисления инициируются вызовом:
x. f ( args)
Фиксирован объект — цель вызова, который и вызывает операцию. Для неквалифицированных вызовов — f(args) неявно заданной целью является объект Current и вызов можно записать в виде Current. f(args).
В ОО-программировании никогда не говорят "Примени эту операцию к тем объектам", что характерно для стиля, отличного от ОО, применяющего вызовы в форме f(x, argl, arg2, ...) со всеми операндами на равной ноге. ОО-программисты говорят "Этот объект применяет операцию, и, если нужны некоторые аргументы, то вот они".
Конечно, все, что выразимо в одном стиле, можно выразить и в другом. Но привычки ОО-стиля, влияющие на структуру программы, глубоки. Напомним только о двух важных понятиях — классе, играющем роль модуля и типа данных, и о наследовании.
Все это прячется в концепциях этого раздела. ОО-программирование является карринг-программированием.