|
Уточните пожалуйста, какие документы для этого необходимо предоставить с моей стороны. Курс "Объектно-ориентированное программирование и программная инженения". |
Универсальность плюс наследование
Введение наследования позволяет нам повторно обратиться к рассмотрению другого главного механизма расширяемости классов — универсальности. Независимо оба механизма уже рассмотрены, их комбинация добавляет новый потенциал.
Полиморфные структуры данных
У нас уже появлялся пример сотрудничества этих механизмов — полиморфные структуры данных. Рассмотрим контейнер, такой как:
fleet: LIST [VEHICLE]
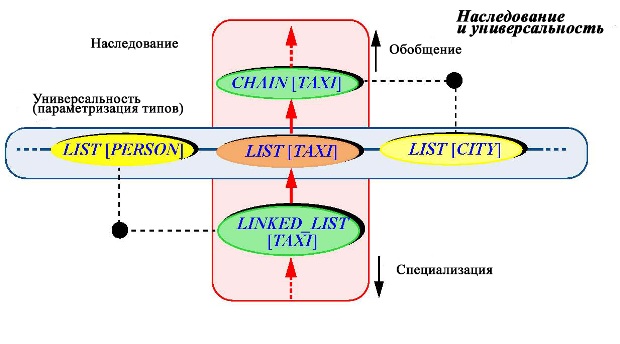
Элементы в контейнере могут быть экземплярами любого из потомков VEHICLE: На следующем рисунке показан графический образ комбинации "универсальность-наследование". Хотя никаких новых концепций не вводится, но здесь иллюстрируется неформальная интерпретация взаимодействия двух механизмов.
Начнем с центра, где показан класс, задающий понятие "список такси", — это класс с ожидаемыми компонентами, характерными для списка: добавить и удалить элемент, передвинуть курсор, получить элемент и так далее. Мы можем перейти теперь к концепции нового класса, двигаясь вдоль двух различных направлений.
- Помимо списка такси интерес могут представлять списки персон, городов, объектов любого другого типа. Универсальность позволяет нам путешествовать по горизонтали, будучи поддержана механизмом параметризации. Важно то, что удается избежать дублирования кода и гарантировать безопасность типов, о чем говорилось в исходном обсуждении этого механизма.
- Список является специальным случаем более общего понятия "цепочка". В свою очередь, специализированным вариантом списка является "связный список", обладающий функциональностью списка, но учитывающий особенности реализации. Наследование позволяет нам путешествовать по вертикали. Оно поддерживается механизмами обобщения и специализации, представляя опять-таки мощную форму повторного использования.
Рисунок иллюстрирует возможность свободного перемещения по метафорической плоскости, переходя от "списка персон" к "цепочке городов".
Ограниченная универсальность
Полиморфные структуры данных не являются единственным способом комбинирования универсальности и наследования. Другая важная техника следует из исследования вопроса: что можно делать с сущностями или выражениями универсального типа?
В универсальном классе, таком как LIST[G] или ARRAY[G], в тексте этого класса, как правило, появляется объявление x: G. Какие операции применимы к G?
Прежнее обсуждение может подсказать ответ. Так как G — просто держатель места для любого типа, который будет задан фактическим родовым параметром ( VEHICLE, например), применимыми операциями могут быть только операции доступные любому типу, следовательно — операции, введенные в классе ANY. Так что можно использовать вызовы: x.cloned, x.isequal(y) и так далее, но нельзя использовать компоненты, отсутствующие у ANY.
Что если требуется больше операций? Рассмотрим случай "сортирующего" класса с методом sort, сортирующим элементы структуры данных, — массива, списка, например, списка целых. Естественно, хочется иметь механизм, работающий для многих типов, а не только для целых. Универсальность кажется подходящим механизмом для реализации поставленной задачи.
Алгоритмы сортировки — это обширная область информатики, она не является предметом нашего изучения, хотя топологическая сортировка была рассмотрена достаточно подробно. Но нет необходимости в разборе различных методов сортировки для осознания того факта, что для сортировки, предположим, массива, понадобится выполнять следующие операторы:
x : = t[i] ; y := t[j]
if x < y then
— Обмен элементов, находящихся в позициях i и j
a [i] := y ; a [j] := x
end
Листинг
4.1.
Алгоритм будет выполнять обмен значениями для элементов, нарушающих порядок. Не интересуясь сейчас тем, как найти такие элементы, сосредоточимся только на одном вопросе: а как выполнить само сравнение, какую операцию "<" следует использовать?
Если речь идет о сортировке целых, то все понятно, но что если необходимо ранжировать игроков в теннис, — как тогда выполняется сравнение? Как быть, если в общем случае мы даже не знаем, есть ли вообще такая операция у объектов?
Иногда мы можем это знать, иногда нет. Как отмечалось при рассмотрении класса COMPARABLE, общепринятого тотального порядка не существует на множестве комплексных чисел или матриц.
Чтобы обеспечить общецелевой алгоритм сортировки, применимый для сортировки массивов с элементами многих типов, можно было бы поместить приведенный ранее код в универсальный класс
class SORTER [G...] feature
sort_array (a: ARRAY [G])
— Сортировка элементов a в соответствии с отношением порядка.
local
x, y: G
do
... Код, такой, как [4] с проверками, такими, как x < y...
End
...
end
Но как быть с операцией "<"? Ведь x и y объявлены как сущности типа G, так что над ними определены только операции из ANY, а там нет операции, позволяющей сравнивать объекты. У нас есть потребность в использовании операции сравнения, но она доступна только для специфических классов, таких как класс COMPARABLE.
Классы, такие как класс COMPARABLE? Почему бы не выбрать сам COMPATIBLE? Он отложен, и его эффективные наследники обеспечат реализацию lesser alias "<". Можно пойти дальше и полагать, что любой класс, объекты которого удовлетворяют отношению тотального порядка, должен быть потомком COMPATIBLE. Тогда ответ на наш вопрос становится очевидным: формальный родовой параметр G не должен быть более произвольным типом, он должен задавать тип, согласованный с COMPATIBLE. Следующий синтаксис позволяет выразить это свойство:
class SORTER [ G -> COMPATIBL] feature ... Остаток как выше...
Символ -> соответствует стрелке на диаграмме наследования, указывая на родительский класс (здесь COMPATIBLE). Вся конструкция в целом задает ограничение универсальности. Смысл ограничения в том, что теперь родовое порождение SORTER[T] является правильным только при условии, что T удовлетворяет ограничению. Так что SORTER[INTEGER] и SORTER[STRING] прекрасно подходят, так же как и SORTER [ TENNIS_PLAYER], при условии, что TENNIS_PLAYER наследует от COMPATIBLE. Но не подходят SORTER [COMPLEX] и SORTER [VEHICLE], если мы только не сделаем транспортные средства сравнимыми. Неподходящие случаи будут отвергнуты на этапе компиляции.
Как вы догадываетесь, базисный случай LIST [G] (неограниченная универсальность) можно рассматривать как краткую форму записи LIST [G-> ANY].
Ограничение универсальности имеет много применений. Некоторые часто встречающиеся случаи используют отложенные библиотечные классы, подобные COMPATIBLE.
- При определении классов, задающих вектора и матрицы, разумно поставлять их с компонентами, реализующими сложение и другие числовые операции. Например, должно быть возможно вычислять ml + m2, где ml и m2 относятся к типу MATRIX[T]. Учитывая тип NUMERIC, к решению приводит объявление: MATRIX[T->NUMERIC]. В этом случае можно использовать MATRIX[INTEGER], но не MATRIX[STRING]. Стоит ли сделать сам класс MATRIX наследником NUMERIC? Этот интересный прием имеет смысл, так как обеспечивает все требуемые операции (модель NUMERIC соответствует математическому понятию кольца ). В этом случае становятся возможными такие родовые порождения классов, как MATRIX[MATRIX[INTEGER]] или MATRIX[MATRIX[MATRIX[REAL]]] и так далее.
- Часто для универсального класса C [T] необходима возможность сохранять элементы типа T в хеш-таблице. Это предполагает, что для каждого такого элемента можно вычислить целочисленную хеш-функцию. Требование простое, но не все типы ему удовлетворяют, нужно иметь дело в этом случае с потомками класса HASHABLE, которые задают реализацию отложенного запроса hashcode.
Сам класс HASHTABLE объявляется как
class HASH_TABLE [ELEMENT, KEY -> HASHABLE] feature...
Теперь становится понятным, почему родовой параметр в классе TOPOLOGICAL_SORTER также был ограничен HASHABLE — мы хотели помещать элементы в хеш-таблицу.
Объявление HASH_TABLE демонстрирует, что универсальный класс может иметь несколько параметров, некоторые из которых могут быть ограниченными. Также ясно, что имена формальных параметров можно выбирать по собственному вкусу.
Замечание : можно задавать множественные ограничения универсальности. Например, можно объявить класс:
class C [G -> (COMPARABLE, NUMERIC, HASHABLE)] feature
Это ограничение говорит, что фактический тип при родовом порождении должен соответствовать всем перечисленным типам. Правильным примером может служить класс INTEGER. Пример немного экстремальный, но требование сравнимости элементов и возможности выполнять над ними числовые операции встречается достаточно часто.
Ограниченная универсальность иллюстрирует фундаментальную роль типов в современном программировании. Для решения обсуждаемых проблем возможны и другие подходы, такие как передача процедуры, выполняющей сравнение, методам класса SORTER. Но данный подход наиболее согласуется с ОО-идеями — сделать требуемую функциональность частью типа. Это также означает, что по-прежнему можно полагаться на компилятор, который будет выполнять все необходимые проверки корректности, что позволит избежать появления подобных ошибок в период выполнения. Если компилятор отвергает ваш класс из-за несогласованности типов, помните, что эта новость, кажущаяся плохой, по-настоящему является хорошей, — лучше вы поймаете "жучка", чем он поймает вас.
Цените мощь статической типизации. Это настоящий механизм верификации программ. Изощренность системы типов, которой вы теперь владеете, — с классами, ограниченной и неограниченной универсальностью, включающей множественные ограничения, одиночное, множественное и повторное наследование, полиморфные переменные и структуры данных, правила вызова методов, передачи аргументов и присваивания, — определяет каркас с математической строгостью, который компилятор использует для выполнения критически важных согласованных проверок. Типы элементов вашей программы отражают семантику, лежащую в основе строящейся модели внешнего мира.