Задачи, сгруппированные по методам решения. Метод вложенных матриц
Рассмотрим задачу.
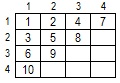
Задача 1: Заполнить двумерный массив размерностью NxN, как показано на рис.9.1 (ряд натуральных чисел указывает на направление обхода элементов):
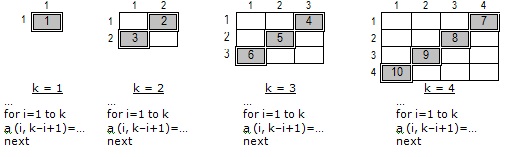
Идея решения: Мысленно "разберем" двумерный массив на четыре "вложенных" в исходный (рис.9.2). В каждом из них нужно заполнить ПОБОЧНУЮ ДИАГОНАЛЬ (опираясь на типовой алгоритм обработки квадратного массива относительно диагоналей):
Итого, k изменяется от 1 до n:
for k=1 to n for i=1 to k a (i,k-i+1)= … next i next k
|
Полное решение задачи на Бейсике: input "n="; n dim a(n,n) x=1 for k=1 to n for i=1 to k a (i,k-i+1)= x x=x+1 next i next k rem===================== for i=1 to n for j=1 to n print a (i,j); next j print next i |
Полное решение задачи на Паскале:
const m=10;
var a: array [1..m, 1..m] of byte;
x, n, k, i: integer;
begin
writeln ('n='); readln (n); x:=1;
for k:=1 to n do
for i:=1 to k do
begin
a [i,k-i+1]:=x;
x:=x+1;
end;
for i:=1 to n do
begin
for j:=1 to n do write (a [i,j]);
writeln;
end;
end.
|
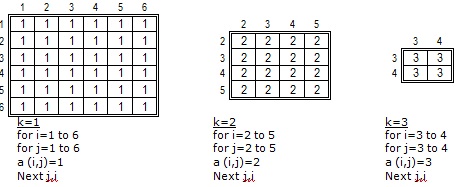
Задача 2: Заполнить массив, как показано на табл.9.1:
Идея решения: Разложим исходную матрицу на "вложенные" (рис.9.3):
Решение задачи на Бейсике:
Input "n="; n Dim a(n,n) for k=1 to n\2+1 for i=k to n-k+1 for j=k to n-k+1 a (i,j)= k next j next i next k rem=====вывод====== for i=1 to n for j=1 to n print a (i,j); next j print next i
Решение задачи на Паскале:
const m=10;
var a: array [1..m, 1..m] of byte;
x, n, k, I, j: integer;
begin
writeln ('n=');
readln (n);
for k:=1 to (n div 2 +1) do
for i:=k to n-k+1 do
for j:=k to n-k+1 do
a [i,j]:= k;
{=======вывод=========}
for i:=1 to n do
begin
for j:=1 to n do
write (a [i,j]);
writeln;
end;
end.Задача 3: Заполнить массив, как показано на табл.9.2:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 20 | 21 | 22 | 23 | 24 | 7 |
| 19 | 32 | 33 | 34 | 25 | 8 |
| 18 | 31 | 36 | 35 | 26 | 9 |
| 17 | 30 | 29 | 28 | 27 | 10 |
| 16 | 15 | 14 | 13 | 12 | 11 |
Дополнительные сведения: На таком заполнении массива базируется задача "скатерть Улама". В данной задаче квадратный массив заполняется по спирали (заполнение происходит не "вовнутрь", как в примере, а "изнутри" массива). Затем "вычеркиваются" все составные числа (см. задачу "Решето Эратосфена"). Оставшиеся на своих местах простые числа образуют причудливый узор, названный в честь автора "Скатертью Улама".
Идея решения: Разложим исходную матрицу на "вложенные". Каждую из "вложенных" матриц необходимо заполнить по периметру (рис.9.4).
Решение на Бейсике:
input "n="; n dim a (n,n) x=1 for k=1 to n\2 for i=k to n-k a(k,i)=x x=x+1 next rem============= for i=k to n-k a(i,n-k+1)=x x=x+1 next rem============= for i=k to n-k a(n-k+1,n-i+1)=x x=x+1 next rem============= for i=k to n-k a(n-i+1,k)=x x=x+1 next i next k rem================= for i=1 to n for j=1 to n print a(i,j); next j print next i
Решение на Паскале:
const m=10;
var a: array [1..m, 1..m] of byte;
x, n, k, i, j: integer;
begin
writeln ('n='); readln (n);
x:=1;
for k:=1 to n div 2 do
begin
for i:=k to n-k do
begin
a [k,i]:=x;
x:=x+1;
end;
for i:=k to n-k do
begin
a [i,n-k+1]:=x;
x:=x+1;
end
for i:=k to n-k do
begin
a [n-k+1,n-i+1]:=x;
x:=x+1;
end ;
for i:=k to n-k do
begin
a [n-i+1,k]:=x;
x:=x+1;
end;
end;
{=======вывод========}
for i:=1 to n do
begin
for j:=1 to n do write (a[i,j]);
writeln;
end;
end.