Обучение по прецедентам (по Вапнику, Червоненкису)
12.5. Сходимость эмпирического риска к среднему. Случай конечного числа решающих правил.
Пусть
-
 – математическое ожидание ошибки классификатора
– математическое ожидание ошибки классификатора 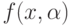 ,
, -
 – событие – ошибка классификатора при решающем правиле
– событие – ошибка классификатора при решающем правиле 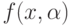 ,
, -
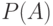 – вероятность,
– вероятность, -
 – частота в
– частота в  испытаниях.
испытаниях.
Воспользуемся неравенством Бернштейна, тогда

Пусть 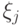 – случайная величина. Тогда
– случайная величина. Тогда 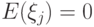 – математическое ожидание
– математическое ожидание 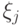 ,
,  – дисперсия, причем
– дисперсия, причем  . Обозначим
. Обозначим 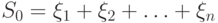 . Тогда соответствующая оценка имеет вид:
. Тогда соответствующая оценка имеет вид:
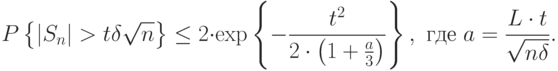
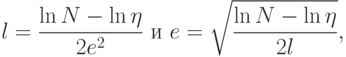
 – необходимое количество прецедентов для обеспечения близости.
– необходимое количество прецедентов для обеспечения близости.Теорема. Пусть из множества, состоящего из  решающих правил, выбирается правило, частота ошибок которого на прецедентах
составляет
решающих правил, выбирается правило, частота ошибок которого на прецедентах
составляет  . Тогда с вероятностью
. Тогда с вероятностью 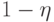 можно утверждать, что вероятность ошибочной классификации с помощью данного
правила
можно утверждать, что вероятность ошибочной классификации с помощью данного
правила 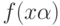 составит величину, меньшую
составит величину, меньшую 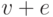 , если длина обучающей последовательности не меньше
, если длина обучающей последовательности не меньше 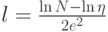 , где
, где  ,
, 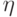 и
и  заданы и
последовательность независима.
заданы и
последовательность независима.
Данная теорема справедлива для случая конечного числа решающих правил. Вапник и Червоненкис смогли обобщить эти оценки на случай бесконечного числа решающих правил.
12.6. Случай бесконечного числа решающих правил
Введем понятие "разнообразия класса функций для бесконечного
множества". Пусть 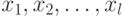 – прецеденты.
– прецеденты.
Определение. Дихотомией называется разбиение множества на два подмножества.
В нашем случае имеем 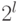 дихотомий. Итак, пусть
дихотомий. Итак, пусть 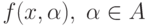 – это класс
решающих правил, причем
– это класс
решающих правил, причем 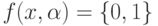 . Пусть
. Пусть 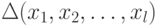 есть количество дихотомий на классе
решающих правил. Тогда зададим энтропию следующим образом:
есть количество дихотомий на классе
решающих правил. Тогда зададим энтропию следующим образом:
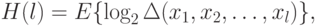
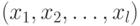 . Тогда
. Тогда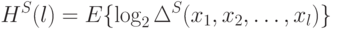
 решающих правил на выборках длины
решающих правил на выборках длины  .
.12.6.1. Критерий равномерной сходимости  к вероятностям
к вероятностям 
Теорема. Для равномерной сходимости 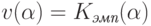 к
к 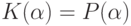 по классу
по классу 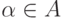 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы ![\frac{H(l)}{l}\xrightarrow[l\rightarrow\infty]{\phantom{0}} 0](/sites/default/files/tex_cache/cc05ec86510ef6a78e5fa3621cd69ba3.png) .
.
Суть данного критерия – не пытаться выделить очень точный классификатор, так как это отдаляет от общности.
Сразу же возникает проблема необходимость перехода к бесконечным системам решающих правил. Существенно, что значение имеет лишь конечное подмножество систем решающих правил, необходимое для разделения конечного числа прецедентов.
12.6.2. Достаточное условие равномерной сходимости
Проверка условия критерия равномерной сходимости по вероятности затрудняется неопределенностью распределения выборки. Поэтому достаточные условия формулируются таким образом, чтобы не зависеть от распределения и при этом гарантировать равномерную сходимость. В таком случае вместо энтропии рассматривается величина:

 – это функция роста класса решающих функций
– это функция роста класса решающих функций 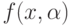 .
.Т.к. логарифм максимума равен максимуму логарифмов, что, в свою очередь, не меньше математического ожидания от логарифма, то
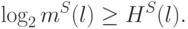
Если
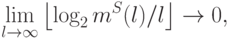
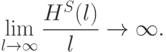
Данное условие легко проверятся для различных классов решающих правил.
Другими словами  можно трактовать как
максимальное число способов разделения
можно трактовать как
максимальное число способов разделения  точек на два
класса с помощью решающих правил
точек на два
класса с помощью решающих правил 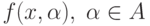 .
.
Теорема. Функция роста либо тождественно равна 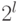 , либо, мажорируется функцией
, либо, мажорируется функцией 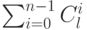 , где
, где  – минимальное значение
– минимальное значение  , при котором
, при котором 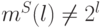 , т.е. либо
, т.е. либо 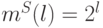 , либо
, либо 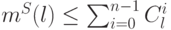 .
.
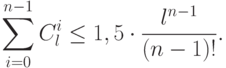
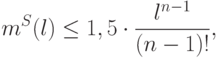
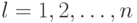 , и
, и 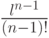 – степенная функция, мажорирующая
– степенная функция, мажорирующая  .
.Существует максимум 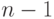 точка, которая еще разбивается всеми
возможными способами с помощью правила
точка, которая еще разбивается всеми
возможными способами с помощью правила 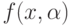 , но никакие
, но никакие  точек этим свойством не обладают.
точек этим свойством не обладают.
Определение. 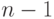 называется емкостью класса
решающих функций или мера разнообразия решающих правил в классе
называется емкостью класса
решающих функций или мера разнообразия решающих правил в классе 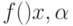 или
или 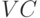 – размерностью класса –
универсальная характеристика класса решающих функций.
– размерностью класса –
универсальная характеристика класса решающих функций.
Отметим, что если 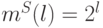 для всех
для всех  ,
то емкость бесконечна.
,
то емкость бесконечна.
Теорема. Если емкость класса решающих функций конечна, то всегда имеет место равномерная сходимость частот к вероятностям такое, что
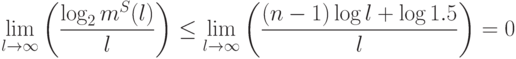
12.6.3. Скорость сходимости
Запишем оценку для бесконечного числа решающих правил. Ее вид аналогичен случаю конечного числа решающих правил:
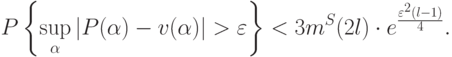
Если емкость бесконечна, то оценка тривиальная (не больше единицы).
Пусть  – конечная емкость класса решающих функций. Тогда
– конечная емкость класса решающих функций. Тогда
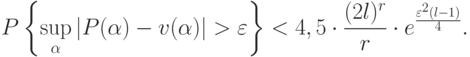
Введем обозначение: 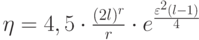 ,
Тогда
,
Тогда  .
.
Отсюда следует, что 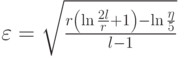 .
.
Значит, с вероятностью, превышающей 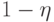 качество эмпирического
оптимального решающего правила отличается от истинно оптимально
решающего правила не более чем на величину
качество эмпирического
оптимального решающего правила отличается от истинно оптимально
решающего правила не более чем на величину 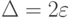 .
.
В следующей таблице представлен некоторый итог наших рассуждений.
| Малая емкость класса решающих функций (бедный) | Большая емкость класса решающих функций (богатый) | |
| Близость эмпирического решающего правила к оптимальному решающему правилу | Хорошая | Плохая |
| Качество разделения (минимизация ошибки) | Низкое | Высокое |
Таким образом, необходимо минимизировать степени свободы.
12.6.4. Случай класса линейных решающих функций
Пусть 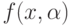 – линейная решающая функция,
– линейная решающая функция,  – размерность пространства.
– размерность пространства.
Как уже отмечалось выше, имеем 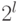 дихотомий, где
дихотомий, где  – длина выборки. Хотим выяснить, какое количество
дихотомий реализуется с помощью гиперплоскостей?
– длина выборки. Хотим выяснить, какое количество
дихотомий реализуется с помощью гиперплоскостей?
Максимальное число точек в пространстве размерности 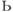 , которое с
помощью гиперплоскостей можно разбить всеми возможными способами на
два класса есть
, которое с
помощью гиперплоскостей можно разбить всеми возможными способами на
два класса есть  . Если
. Если 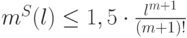 ,
то линейный риск будет равномерно сходиться
к среднему риску. Емкость класса конечна и равна
,
то линейный риск будет равномерно сходиться
к среднему риску. Емкость класса конечна и равна 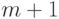 .
.
