Метод потенциальных функций
6.1. Общая рекуррентная процедура
Пусть 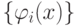 – конечная или
бесконечная система функций на
– конечная или
бесконечная система функций на  . Будем искать дискриминантную функцию
в виде
. Будем искать дискриминантную функцию
в виде
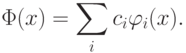
Требования к рассматриваемому ряду:
Для бесконечного ряда требуем поточечную сходимость.
Также желательно, чтобы 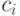 убывали быстро с ростом
убывали быстро с ростом  . Это необходимо для обеспечения хорошего совпадения
"обрезанного" бесконечного ряда с
. Это необходимо для обеспечения хорошего совпадения
"обрезанного" бесконечного ряда с 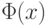 .
.
Итак, пусть 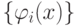 – базовая система функций. В качестве потенциальной
функции будем рассматривать функцию вида
– базовая система функций. В качестве потенциальной
функции будем рассматривать функцию вида
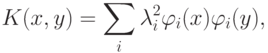
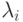 удовлетворяет условиям:
удовлетворяет условиям: 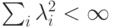 и
и  . Обозначим
. Обозначим 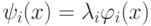 . Тогда
. Тогда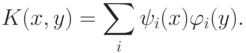
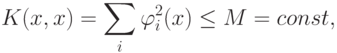

Для приближения 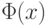 предлагается рекуррентная процедура, называемая
общей рекуррентной процедурой:
предлагается рекуррентная процедура, называемая
общей рекуррентной процедурой:
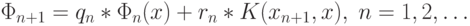
Пусть
-
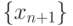 – обучающая последовательность прецедентов;
– обучающая последовательность прецедентов; -
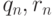 – некоторые числовые последовательности, которые должны задаваться так, чтобы обеспечить сходимость
– некоторые числовые последовательности, которые должны задаваться так, чтобы обеспечить сходимость 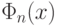 к
к 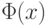 при
при 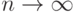 в том или ином смысле.
в том или ином смысле.
Зададим начальное приближение  . Как уже отмечалось, мы ищем
функцию
. Как уже отмечалось, мы ищем
функцию 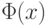 в виде:
в виде:
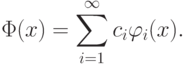
Мы сделали достаточно сильное допущение, сказав, что наше решение
будем выражать через базовую систему функций. Т.е. мы априорно
предполагаем, что 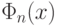 разложимо по системе функций
разложимо по системе функций 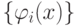 :
:
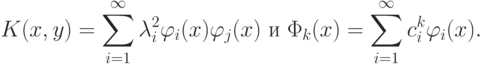
Тогда, учитывая, что 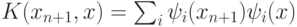 , получаем:
, получаем:
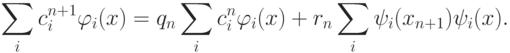
Обозначим через
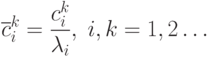
Тогда

Откуда получаем вторую форму общей рекуррентной процедуры:
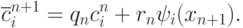
Для нахождения связи коэффициентов 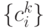 и
и  воспользуемся второй
формой для формулы общей рекуррентной процедуры и соотношением
воспользуемся второй
формой для формулы общей рекуррентной процедуры и соотношением
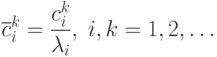
Получим соотношение, связывающее коэффициенты 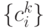 и
и  :
:
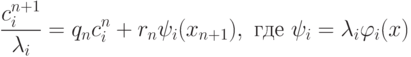
Для возможности итерационных вычислений необходимо понять, как
вычислять параметры 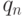 и
и 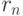 , а также начальное приближение
, а также начальное приближение  .
.
Зададим функцию
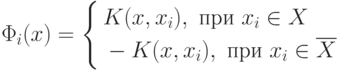

Тогда процесс перехода от 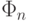 к
к  суть процесс подсчета
коэффициентов. Обычно
суть процесс подсчета
коэффициентов. Обычно 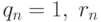 , вычисляется по следующему правилу:
, вычисляется по следующему правилу:
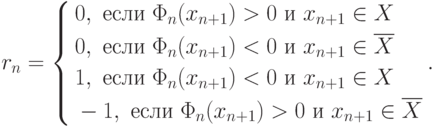
Возьмем следующее начальное приближение:
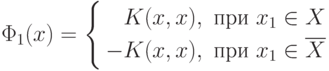
Таким образом, при правильном определении  получаем,
что
получаем,
что 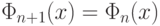 ; а в случае ошибки
; а в случае ошибки
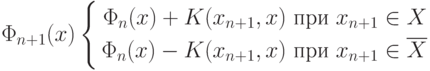
Данный процесс напоминает обучение в алгоритме персептрона.
Возникают следующие естественные вопросы:
Есть ли поточечная сходимость функции 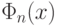 к
к 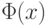 ?
?
Где взять базисные функции 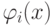 в многомерном пространстве?
в многомерном пространстве?
Попробуем ответить на эти вопросы.
Рассмотрим аналогию данного алгоритма с алгоритмом персептрона. Для функции
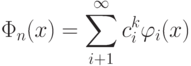
 и
и 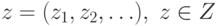 – это вектор в бесконечномерном пространстве, тогда
– это вектор в бесконечномерном пространстве, тогда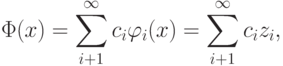
 – спрямляющее пространство. Таким образом, если
– спрямляющее пространство. Таким образом, если 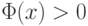 или
или  , то
, то  или
или  соответственно. Пусть
соответственно. Пусть 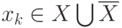 ,
тогда
,
тогда 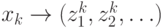 и
и 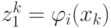 .
.