Рекуррентные сети: Ассоциативная память
Ассоциативная память
Аттракторами сети Хопфилда являются стационарные состояния. Если начальная конфигурация  мало отличается от одного из таких
аттракторов сети
мало отличается от одного из таких
аттракторов сети 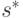 (т.е.
(т.е. 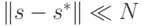 ), то она быстро эволюционирует к этому ближайшему аттрактору, изменив состояния небольшого числа нейронов.
Такой переход можно записать в виде
), то она быстро эволюционирует к этому ближайшему аттрактору, изменив состояния небольшого числа нейронов.
Такой переход можно записать в виде  . Можно проинтерпретировать это явление так, что состояние
. Можно проинтерпретировать это явление так, что состояние  содержит частичную, неполную
информацию, которая, однако, достаточна для восстановления полной информации, кодируемой состоянием
содержит частичную, неполную
информацию, которая, однако, достаточна для восстановления полной информации, кодируемой состоянием 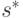 . Например, мы способны
восстановить название города по неполному набору букв В*нец*я. Такая память, в которой информация ищется не по формальному адресу
(подобно поиску книги в библиотеке по ее шифру), а на основе частичной информации о ее содержании, называется адресованной по
содержанию. Таким образом модель Хопфилда может использоваться для имитации содержательно-адресованной или, иными словами,
ассоциативной памяти.
. Например, мы способны
восстановить название города по неполному набору букв В*нец*я. Такая память, в которой информация ищется не по формальному адресу
(подобно поиску книги в библиотеке по ее шифру), а на основе частичной информации о ее содержании, называется адресованной по
содержанию. Таким образом модель Хопфилда может использоваться для имитации содержательно-адресованной или, иными словами,
ассоциативной памяти.
Важным свойством такой памяти, представленной набором аттракторов сети, является ее распределеннсть. Это означает, что все нейроны сети участвуют в кодировании всех состояний памяти. Поэтому небольшие искажения значений отдельных весов не сказываются на содержании памяти, что повышает устойчивость памяти к помехам.
Конечно, ассоциативная память может быть реализована и без использования нейронных сетей. Для этого достаточно с помощью обычного компьютера осуществить последовательное сравнение внешнего стимула со всеми предварительно запомненными образами, выбрав из них тот, для которого Хэммингово расстояние до входного сигнала минимально. Однако, сеть Хопфилда позволяет исключить перебор состояний памяти и осуществить эту процедуру параллельным способом, при котором время выборки из памяти не увеличивается с ростом числа запомненных образов.
Обучение сети. Правило Хебба
Описанная сеть действительно стала использоваться для моделирования ассоциативной памяти, поскольку уже в первой своей работе Хопфилд указал конструктивный метод построения синаптических связей между нейронами, который в некоторых случаях позволял запомнить любые заранее заданные состояния сети.
Например, полезной была бы сеть, аттракторы которой, соответствовали бы векторам, кодирующим бинарные изображения подписей
различных людей на чеке. Поскольку практически невозможно одинаково расписаться дважды, подобная сеть была бы незаменима при
распознавании подписи, несмотря на ее естественные вариации. Если число различных типов подписей, которые должна распознавать сеть,
равно P и образцы в некотором смысле типичных, наиболее вероятных или усредненных подписей различных людей кодируются векторами 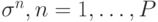 , то
желательно, чтобы именно эти векторы кодировали и аттракторы сети, которую мы собираемся использовать для классификации.
, то
желательно, чтобы именно эти векторы кодировали и аттракторы сети, которую мы собираемся использовать для классификации.
Хопфилд предложил использовать для решения этой задачи Хеббовское правило построения межнейронных связей2Ранее мы определяли обучение по Хеббу как такое, при котором изменение веса  пропорционально j - му входу и выходу i-го нейрона. В рекуррентной сети Хопфилда состояниие j-го нейрона как раз и является j-м входом для остальных нейронов.
пропорционально j - му входу и выходу i-го нейрона. В рекуррентной сети Хопфилда состояниие j-го нейрона как раз и является j-м входом для остальных нейронов.
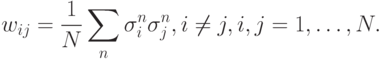
Это правило действительно гарантирует стационарность произвольно выбранных векторов 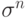 в случае, когда их число
в случае, когда их число  не превосходит
примерно 5% от общего числа нейронов
не превосходит
примерно 5% от общего числа нейронов  . При больших значениях
. При больших значениях  некоторые из запоминаемых векторов
некоторые из запоминаемых векторов 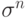 теряют свойство стационарности,
а при превышении некоторого критического значения - емкости памяти - (
теряют свойство стационарности,
а при превышении некоторого критического значения - емкости памяти - ( 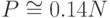 ) стационарные состояния сети теряют всякую связь с ними, и
сеть переходит из режима запоминания в режим спинового стекла, для которого характерно наличие очень большого числа аттракторов,
далеких от любых запоминаемых векторов. Эти свойства модели Хопфилда были открыты с использованием математического аппарата
статистической физики. Заинтересованный читатель может ознакомиться с этим подходом более подробно в последней, дополнительной,
лекции этого курса.
) стационарные состояния сети теряют всякую связь с ними, и
сеть переходит из режима запоминания в режим спинового стекла, для которого характерно наличие очень большого числа аттракторов,
далеких от любых запоминаемых векторов. Эти свойства модели Хопфилда были открыты с использованием математического аппарата
статистической физики. Заинтересованный читатель может ознакомиться с этим подходом более подробно в последней, дополнительной,
лекции этого курса.
Аттракторам, не совпадающим с векторами 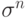 , часто присваиваются такие негативные названия, как ложная или паразитная память,
химеры, русалки и даже мусорная куча. Подобное отношение вызвано тем, что при релаксации начального состояния сети в одно из
состояний ложной памяти интерпретировать результат распознавания становится затруднительно. Однако само по себе появление таких
непредвиденных аттракторов является замечательным свойством модели Хопфилда и свидетельствует о том, что она способна не просто на
ассоциативную выборку запомненной информации, но также и на синтез новых образов. Можно сказать, что сеть активно преобразует исходную
информацию, а не является пассивным хранилищем образов. Ниже мы покажем, как можно интерпретировать все аттракторы сети единым
образом, и приведем примеры, когда т.н. ложная память играет позитивную роль.
, часто присваиваются такие негативные названия, как ложная или паразитная память,
химеры, русалки и даже мусорная куча. Подобное отношение вызвано тем, что при релаксации начального состояния сети в одно из
состояний ложной памяти интерпретировать результат распознавания становится затруднительно. Однако само по себе появление таких
непредвиденных аттракторов является замечательным свойством модели Хопфилда и свидетельствует о том, что она способна не просто на
ассоциативную выборку запомненной информации, но также и на синтез новых образов. Можно сказать, что сеть активно преобразует исходную
информацию, а не является пассивным хранилищем образов. Ниже мы покажем, как можно интерпретировать все аттракторы сети единым
образом, и приведем примеры, когда т.н. ложная память играет позитивную роль.
Модель Крика - Митчисона. Разобучение
В 1983 году в журнале Nature одновременно появились две публикации (Hopfield, Feinstein & Palmer 1983 и Crick & Mitchison,
1983), в которых была описана процедура уменьшения доступа к состояниям ложной памяти и ее возможная биологическая интерпретация. Эта
процедура, названная разобучением, применяется к уже обученной сети, в пространстве которой есть ложные состояния. Она предполагает
многократное предъявление сети в качестве начальных состояний случайно сгенерированных векторов и прослеживание их эволюции вплоть до
стационарного состояния 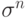 , которое может принадлежать как истинной, так и ложной памяти. После этого связи в сети модифицируются
следующим образом:
, которое может принадлежать как истинной, так и ложной памяти. После этого связи в сети модифицируются
следующим образом: 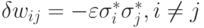 , где
, где 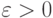 - небольшая константа.
- небольшая константа.
Хопфилд с коллегами установили, что применение такой процедуры к сети, обученной по правилу Хебба на наборе случайных векторов, приводит к увеличению и выравниванию доступности состояний, соответствующих запоминаемым образам, и снижению доступности состояний ложной памяти. Эти явления они объяснили тем, что в рассматриваемом случае состояниям ложной памяти соответствуют гораздо более "мелкие" энергетические минимумы, чем состояниям, соответствующим запоминаемым образам. Поэтому ложные состояния сильнее подвержены разобучению, которое выражается в "закапывании" энергетических минимумов, в которые попадает система. Выравнивание доступности состояний памяти объясняется тем, что состояния с большими областями притяжения чаще притягивают случайный стимул и их область притяжения уменьшается быстрее, чем у состояний с меньшими сферами притяжения.
Крик и Митчисон, кроме того, предположили, что процесс, аналогичный разобучению, происходит в мозгу человека и животных во время фазы быстрого (парадоксального) сна, для которого характерны фантастические сюжеты (составленные из аналогов ложных образов). В этот период кора головного мозга постоянно возбуждается случайными воздействиями ствола мозга, и возникающие картины далеки от тех, которые дает сенсорный опыт. Разобучение при этом эффективно приводит к забыванию подобных парадоксальных картин и к увеличению доступа к образам, соответствующим объектам внешнего мира. Гипотеза о роли быстрого сна была сформулирована Криком и Митчисоном в виде афоризма: "Мы грезим, чтобы забыть".
Идея разобучения затем была развита другими исследователями. В одном из ее вариантов в качестве начальных состояний сети
предъявляются не случайные стимулы, а зашумленные случайным шумом запоминаемые образы. При этом, помимо разобучения сети финальным
аттрактором, она слегка подучивается запоминаемым образом 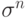
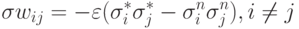
То есть, если образ памяти восстанавливается без ошибки, синаптические связи не модифицируются. Подобная модификация процедуры
разобучения может существенно увеличить емкость памяти (с 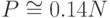 до
до  ).
).
