Рекуррентные сети: Ассоциативная память
Сеть Хопфилда как ассоциативная память
Симметричность связей
В Хопфилдовской сети матрица связей между нейронами  является полной и симметричной (
является полной и симметричной (  ) а самовоздействие нейронов считается
отсутствующим (
) а самовоздействие нейронов считается
отсутствующим ( 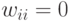 ). Подобные свойства определяют тесную связь модели со спиновыми стеклами. Критики отмечают, что подобная ориентация
на физические системы делает модель несостоятельной с физиологической точки зрения (хотя в мозге существуют некоторые структурные
единицы - колонки, связи между нейронами в которых не так уж далеки от симметричных). Однако, самое главное в таком подходе то, что
простота архитектуры сети облегчает имитацию с ее помощью богатого спектра явлений, которые могут быть соотнесены с реальными
свойствами мозга.
). Подобные свойства определяют тесную связь модели со спиновыми стеклами. Критики отмечают, что подобная ориентация
на физические системы делает модель несостоятельной с физиологической точки зрения (хотя в мозге существуют некоторые структурные
единицы - колонки, связи между нейронами в которых не так уж далеки от симметричных). Однако, самое главное в таком подходе то, что
простота архитектуры сети облегчает имитацию с ее помощью богатого спектра явлений, которые могут быть соотнесены с реальными
свойствами мозга.
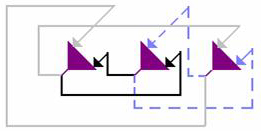
Рис. 5.3. Архитектура сети Хопфилда. Связи с одинаковым весом обозначены одинаковыми линиями. Матрица соединений полносвязанная и симметричная. Самовоздействие нейронов отсутствует
Асинхронная динамика
Нейроны в модели Хопфилда, подобно спиновым переменным, могут принимать два состояния 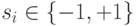 , а динамика состояний сети носит асинхронный
характер (т.н. Глауберова динамика). В дискретные моменты времени
, а динамика состояний сети носит асинхронный
характер (т.н. Глауберова динамика). В дискретные моменты времени 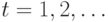 случайным образом выбирается один нейрон (k-ый) для которого
вычисляется значение потенциала
случайным образом выбирается один нейрон (k-ый) для которого
вычисляется значение потенциала
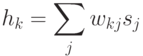
При выполнении условия 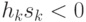 состояние нейрона изменяется на противоположное:
состояние нейрона изменяется на противоположное: 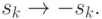
В другом варианте - последовательной динамике - перебор нейронов производится не случайным образом а циклически, но в каждый
момент времени также может изменяться состояние лишь одного нейрона. Эти два варианта качественно отличаются от параллельной динамики,
подразумевающей одновременное изменение состояний всех тех нейронов, для которых выполняется условие 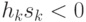 (такова, например, динамика
модели Литтла). Синхронизация моментов обновления состояний нейронов делает такую динамику подверженной "зацикливаниям".
(такова, например, динамика
модели Литтла). Синхронизация моментов обновления состояний нейронов делает такую динамику подверженной "зацикливаниям".
В отличие от многослойных сетей, в которых входные и выходные нейроны пространственно разделены в модели Хопфилда все нейроны одновременно являются и входными, и скрытыми, и выходными. Роль входа в таких сетях выполняет начальная конфигурация активностей нейронов, а роль выхода - конечная стационарная конфигурация их активностей.
Метрика пространства состоянний
Расстояние между состояниями сети можно измерять в т.н. метрике Хэмминга. Если два вектора 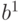 и
и 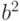 бинарные, то Хэммингово
расстояние между ними определяется как количество различающихся компонент. Так, если векторы имеют вид
бинарные, то Хэммингово
расстояние между ними определяется как количество различающихся компонент. Так, если векторы имеют вид 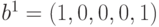 и
и 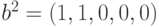 ,
то Хэммингово расстояние между ними
,
то Хэммингово расстояние между ними 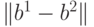 будет равно двум, поскольку в точности две компоненты этих векторов (вторая и пятая) имеют
различные значения. Формально, Хэммингово расстояние для таких (Булевых) векторов может быть определено как
будет равно двум, поскольку в точности две компоненты этих векторов (вторая и пятая) имеют
различные значения. Формально, Хэммингово расстояние для таких (Булевых) векторов может быть определено как
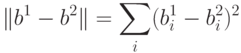
В случае спиновых переменных, 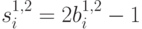 , принимающих значения
, принимающих значения  , расстояние Хэмминга может быть переписано в виде
, расстояние Хэмминга может быть переписано в виде
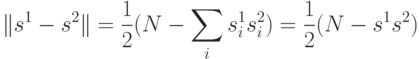
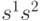 - скалярное произведение, или перекрытие между векторами
- скалярное произведение, или перекрытие между векторами 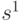 и
и 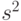 . Таким образом, минимальное Хэммингово расстяние между векторами со
спиновыми переменными соответствует максимальному перекрытию между ними.
. Таким образом, минимальное Хэммингово расстяние между векторами со
спиновыми переменными соответствует максимальному перекрытию между ними.Энергия состояния
Нетрудно показать, что описанная выше асинхронная динамика сети сопровождается уменьшением энергии сети, которая определяется следующим образом:
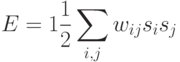
Действительно, при изменении состояния одного k-го нейрона его вклад в энергию изменяется с 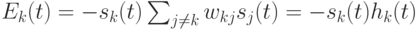 на
на  Следовательно,
Следовательно,
![E_k(t+1)=-sgn[h_k(t)]h_k(t)=-|h_k(t)|\leq -s_k(t)h_k(t)=E_k(t).](/sites/default/files/tex_cache/446308b4b8b46ecc616fa9f3d92543dd.png)
В случае, когда нейроны имеют ненулевые пороги активации 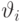 , энергия состояния приобретает вид
, энергия состояния приобретает вид 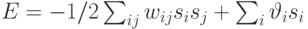 , но вышеприведенный вывод остается в силе.
, но вышеприведенный вывод остается в силе.
Поскольку число нейронов в сети конечно, функционал энергии ограничен снизу. Это означает, что эволюция состояния сети должна закончиться в стационарном состоянии, которому будет соответствовать локальный минимум энергии. В Хопфилдовской модели стационарные конфигурации активностей нейронов являются единственным типом аттракторов в пространстве состояний сети. Мы можем представить динамику сети, сопоставив ее состояние с шариком, движущимся с большим трением в сложном рельефе со множеством локальных минимумов. Сами эти минимумы будут устойчивыми состояниями памяти, а окружающие точки на склонах - переходными состояниями.
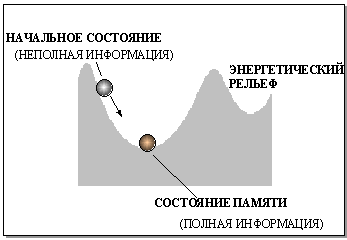
Рис. 5.4. Поведение состояния в сети Хопфилда аналогично движению шарика, скатывающегося со склона в ближайшую лунку. Начальное состояние шарика соответствует вектору, содержащему неполную информацию об образе памяти, которому отвечает дно лунки
Такая динамика определяет главное свойство сети Хопфилда - способность восстанавливать возмущенное состояние равновесия - "вспоминать" искаженные или потерянные биты информации. Восстановление полной информации по какой-либо ее части - вспоминание по ассоциации - наделяет модель Хопфилда свойством ассоциативной памяти. (Далее в этой лекции мы продемонстрируем, и более общие возможности сети Хопфилда.)
