Опубликован: 12.02.2014 | Доступ: свободный | Студентов: 924 / 239 | Длительность: 11:22:00
Тема: Программирование
Специальности: Программист
Лекция 9:
Деревья
Упражнение 1. Определите предикат, который проверяет принадлежность элемента двоичному дереву.
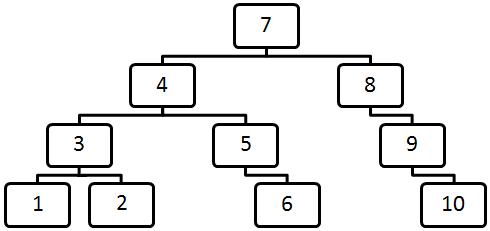
Двоичное дерево поиска — это конечное корневое дерево, в котором элементы левого поддерева любой вершины меньше этой вершины, а элементы правого поддерева не меньше нее. На рис. 9.2 приведен пример двоичного дерева поиска.
В следующей программе генерируется случайным образом двоичное дерево поиска с вершинами, в которых хранятся целые неотрицательные числа, а также реализуются операции над двоичными деревьями.
Предикат insert/2 вставляет элемент в двоичное дерево поиска так, чтобы оно оставалось деревом поиска. Предикат get_nd/2 недетерминированно возвращает вершины заданного уровня. Предикат height/1 возвращает высоту дерева, предикат height_nd/2 недетерминированно возвращает высоту ветвей дерева. Высота дерева определяется как максимальная из высот ветвей. Предикаты sum/1 и count/1 вычисляют соответственно сумму элементов дерева и количество четных вершин. В подсчетах используются накопители. Предикат replace/3 заменяет элементы дерева с заданным значением другими элементами.
domains
binTree{Elem} = bt(binTree{Elem}, Elem, binTree{Elem}); leaf.
class predicates % построение дерева предков
createBinTree: (unsigned, positive) -> binTree{unsigned}.
createBinTree: (unsigned, positive, binTree{unsigned})
-> binTree{unsigned}.
insert: (Elem, binTree{Elem}) -> binTree{Elem}.
clauses
createBinTree(R, N) = createBinTree(R, N, leaf).
createBinTree(_, 0, Tree) = Tree:- !.
createBinTree(R, N, Tree) =
createBinTree(R, N - 1, insert(math::random(R), Tree)).
insert(X, leaf) = bt(leaf, X, leaf).
insert(X, bt(LTree, Y, RTree)) = bt(insert(X, LTree), Y, RTree):-
X < Y,
!.
insert(X, bt(LTree, Y, RTree)) = bt(LTree, Y, insert(X, RTree)).
class predicates
print: (binTree{Elem}).
print: (binTree{Elem}, charCount).
clauses
print(BinTree):-
print(BinTree, 0).
print(leaf, _).
print(bt(LeftTree, Elem, RightTree), N):-
print(LeftTree, N + 1),
write(string::create(N, "\t"), Elem), nl,
print(RightTree, N + 1).
class predicates % вершины заданного уровня
get_nd: (binTree{Elem}, positive) -> Elem nondeterm.
clauses
get_nd(bt(_, A, _), 0) = A:- !.
get_nd(bt(LTree, _, _), N) = get_nd(LTree, N - 1).
get_nd(bt(_, _, RTree), N) = get_nd(RTree, N - 1).
class predicates % высота дерева
height: (binTree{Elem}) -> integer.
height_nd: (binTree{Elem}, integer) -> integer nondeterm.
clauses
height(Tree) = list::maximum([N || N = height_nd(Tree, -1)]).
height_nd(leaf, N) = N.
height_nd(bt(LTree, _, _), N) = height_nd(LTree, N + 1).
height_nd(bt(_, _, RTree), N) = height_nd(RTree, N + 1).
class predicates % подсчеты
sum: (binTree{unsigned}) -> unsigned.
sum: (binTree{unsigned}, unsigned) -> unsigned.
count: (binTree{unsigned}) -> positive.
count: (binTree{unsigned}, positive) -> positive.
clauses
sum(Tree) = sum(Tree, 0). % сумма всех вершин
sum(leaf, N) = N.
sum(bt(LTree, A, RTree), N) = sum(RTree, sum(LTree, N) + A).
count(Tree) = count(Tree, 0). % количество четных вершин
count(leaf, N) = N.
count(bt(LTr, A, RTr), N) = count(RTr, count(LTr, N) + C):-
C = if A mod 2 = 0 then 1 else 0 end if.
class predicates % замена заданных вершин
replace: (binTree{unsigned}, unsigned, unsigned)
-> binTree{unsigned}.
clauses
replace(leaf, _, _) = leaf.
replace(bt(LTree, V, RTree), A, B) =
bt(replace(LTree, A, B), C, replace(RTree, A, B)):-
C = if V = A then B else V end if.
run():-
Tree = createBinTree(20, 20),
print(Tree),
write("\n\nПоколение 3: ", [Elem || Elem = get_nd(Tree, 3)]),
write("\nВысота дерева: ", height(Tree)),
write("\nСумма элементов дерева: ", sum(Tree)),
write("\nКоличество четных вершин дерева: ", count(Tree)),
write("\nЗамена нулевых элементов на 100:\n\n"),
Tree1 = replace(Tree, 0, 100),
print(Tree1),
_ = readLine().
Пример
9.3.
Двоичное дерево поиска
Предикат maximum возвращает максимальный элемент списка.
