Рекурсия

Рекурсивное программирование является в логических языках основным видом программирования. Эффективность рекурсивных программ повышается с помощью хвостовой рекурсии. В большинстве декларативных языков программирования имеется оптимизация хвостовой рекурсии.

В настоящей главе рассматриваются виды рекурсии и рекурсивные алгоритмы. Кроме этого, вводятся понятие функции и понятие предикатного домена в языке Visual Prolog.

5.1. Рекурсивное определение отношений

Определение рекурсивного предиката состоит в указании базиса рекурсии и шага рекурсии, так что в нем участвуют как рекурсивные правила, в которых предикат описывается через самого себя, так и правила, не являющиеся рекурсивными.

Основным недостатком рекурсивного программирования является большой расход памяти. Для каждого вызова рекурсивного предиката запоминается его состояние, чтобы можно было вернуться к нему впоследствии.

Рассмотрим определение факториала целого неотрицательного числа:

.

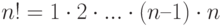Очевидно, что 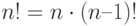. Соответственно, определим рекурсивно предикат fact/2 следующим образом:

class predicates
    fact: (positive, unsigned64 [out]).
clauses
    fact(0, 1):- !.            % 1 правило
    fact(N, F):- fact(N - 1, X), F = N * X.    % 2 правило

Проследим ход поиска решений для цели

fact(3, R).

Данная цель не унифицируется с заголовком первого правила, но унифицируется с заголовком второго правила, которое имеет вид (напомним, что переменные в правилах автоматически переименовываются):

fact(N1, F1):- fact(N1 - 1, X1), F1 = N1 * X1.
Имеем: N1 = 3, F1 = R. Новая цель имеет вид:
fact(2, X1), R = 3 * X1.

Сначала вызывается подцель

fact(2, X1).

Она также не унифицируется с заголовком первого правила, но унифицируется с заголовком второго:

fact(N2, F2):- fact(N2 - 1, X2), F2 = N2 * X2.

При этом N2 = 2, F2 = X1. Следующая цель имеет вид:

fact(1, X2), X1 = 2 * X2, R = 3 * X1.

Вызывается подцель

fact(1, X2).

Эта подцель также унифицируется с заголовком только второго правила:

fact(N3, F3):- fact(N3 - 1, X3), F3 = N3 * X3.

При этом N3 = 1, F3 = X2. Следующая цель выглядит так:

fact(0, X3), X2 = 1 * X3, X1 = 2 * X2, R = 3 * X1.

Вызывается первая подцель

fact(0, X3).

Она унифицируется с заголовком правила

fact(0, 1):- !.

При этом X3 = 1. В теле этого правила стоит отсечение, поэтому других решений быть не может. Полученное значение передается в оставшуюся цель

X2 = 1 * X3, X1 = 2 * X2, R = 3 * X1.

Из первой подцели находится значение X2 = 1. Оно передается в цель

X1 = 2 * X2, R = 3 * X1.

Из первой подцели следует, что X1 = 2. Это значение передается в цель

R = 3 * X1.

Таким образом, получено решение

R = 6.

Данная рекурсия является нисходящей. Нисходящая рекурсия последовательно разбивает задачу на все более простые, пока не доходит до граничной ситуации, в которой уже не требуется продолжения рекурсии.

В целях повышения эффективности вычислений перейдем к хвостовой рекурсии. Рекурсия — хвостовая, если вызов предиката самого себя идет последним в правиле, при этом до него нет недетерминированных вызовов. Хвостовая рекурсия соответствует итерации в процедурных языках программирования.