Внешний поиск

Программа 16.2. Поиск в B-дереве

Как обычно, эта реализация операции найти для B-деревьев выполнена рекурсивной. Для внутренних узлов (имеющих положительную высоту) выполняется поиск ключа, который больше искомого, а затем рекурсивный вызов для поддерева, указанного предыдущей ссылкой. Для внешних узлов (высота которых равно 0) выполняется просмотр, чтобы выяснить, содержат ли они элемент с ключом, равным искомому.

private:
  Item searchR(link h, Key v, int ht)
    { int j;
      if ( ht == 0)
        for (j = 0; j < h->m; j++)
          { if (v == h->b[j].key)
            return h->b[j].item;
          }
      else
        for (j = 0; j < h->m; j++)
          if ((j + 1 == h->m) || (v < h->b[j + 1].key))
            return searchR(h->b[j].next, v, ht-1);
      return nullItem;
    }
public:
  Item search(Key v)
    { return searchR(head, v, HT); }
      

Программа 16.3. Вставка в B-дерево

При вставке новых элементов большие элементы сдвигаются вправо на одну позицию, как в сортировке вставками. Если вставка приводит к переполнению узла, вызывается функция split для разбиения узла пополам, а затем ссылка на новый узел вставляется во внутренний родительский узел, который также может потребовать разбиения; таким образом, влияние вставки может распространиться вплоть до корня.

private:
  link insertR(link h, Item x, int ht)
    { int i, j; Key v = x.key(); entry<Item, Key> t;
      t.key = v; t.item = x;
      if (ht == 0)
        for (j = 0; j < h->m; j++)
          { if (v < h->b[j].key) break; }
      else
        for (j = 0; j < h->m; j++)
          if ((j+1 == h->m) || (v < h->b[j+1].key))
            { link u;
              u = insertR(h->b[j++].next, x, ht-1);
              if (u == 0) return 0;
              t.key = u->b[0].key; t.next = u; break;
            }
      for (i = h->m; i > j; i—) h->b[i] = h->b[i-1];
      h->b[j] = t;
      if (++h->m < M) return 0; else return split(h);
    }
public:
  ST(int maxN)
    { N = 0; HT = 0; head = new node; }
  void insert(Item item)
    { link u = insertR(head, item, HT);
      if (u == 0) return;
      link t = new node(); t->m = 2;
      t->b[0].key = head->b[0].key;
      t->b[1].key = u->b[0].key;
      t->b[0].next = head;
      t->b[1].next = u;
      head = t; HT++;
    }
      

Программа 16.4. Разбиение узла B-дерева

Для разбиения узла в B-дереве создается новый узел, и большая половина ключей перемещается в новый узел, а затем корректируются счетчики, и в середины обоих узлов заносятся сигнальные ключи. В этой программе предполагается, что M четно, а в каждом узле имеется лишняя позиция для элемента, вызвавшего разбиение. То есть максимальное количество ключей в узле равно M-1, а когда количество ключей в узле достигает M, он разбивается на два узла с M/2 ключами в каждом.

  link split(link h)
    { link t = new node();
      for (int j = 0; j < M/2; j++)
        t->b[j] = h->b[M/2+j];
      h->m = M/2; t->m = M/2;
      return t;
    }
      

Если M равно 1000, то при N, меньшем 125 миллионов, высота дерева меньше трех. В типичных ситуациях можно хранить корневой узел в оперативной памяти и этим уменьшить затраты до двух проб. Для реализаций поиска на диске этот шаг можно предпринимать явно перед запуском любого приложения, связанного с очень большим количеством поисков; в виртуальной памяти с кэшированием корневым узлом будет узел, который вероятнее всего находится в быстрой памяти, т.к. это узел, к которому происходит наибольшее количество обращений.

Вряд ли можно рассчитывать на реализацию поиска, которая сможет гарантировать выполнение менее двух проб для выполнения операций найти и вставить в очень больших файлах, и B-деревья находят широкое применение, поскольку они позволяют приблизиться к этому идеалу. Однако производительность и гибкость достигаются ценой неиспользуемой памяти внутри узлов, что для очень больших файлов может оказаться обременительным.

Лемму 16.3 можно также проверить, написав программу для моделирования вероятностного процесса (см. упражнение 16.11 и рис. 16.8 и 16.9). Конечно, можно также просто строить случайные B-деревья и измерять их структурные характеристики. Вероятностное моделирование выполнить проще, чем провести математический анализ или создать полную реализацию, кроме того, оно служит важным инструментом изучения и сравнения вариантов алгоритмов (см., например, упражнение 16.16).

Реализации других операций такой таблицы символов аналогичны соответствующим реализациям для других ранее рассмотренных представлений с использованием деревьев и оставлены в качестве упражнений (см. упражнения 16.22—16.25). В частности, реализации операций выбрать и сортировать очевидны, но, как обычно, правильная реализация операции удалить может оказаться сложной задачей. Подобно операции вставить, большинство операций удалить сводятся к простому удалению элемента из внешней страницы и уменьшению значения ее счетчика; но что делать, если необходимо удалить элемент из узла, который имеет только M/2 элементов? Естественный подход — найти для заполнения свободного места элементы в родственных узлах (возможно, с уменьшением количества узлов на единицу), но тогда реализация усложняется, поскольку приходится отслеживать ключи, связанные со всеми перемещаемыми по узлам элементами.

Рис. 16.8. Рост большого B-дерева

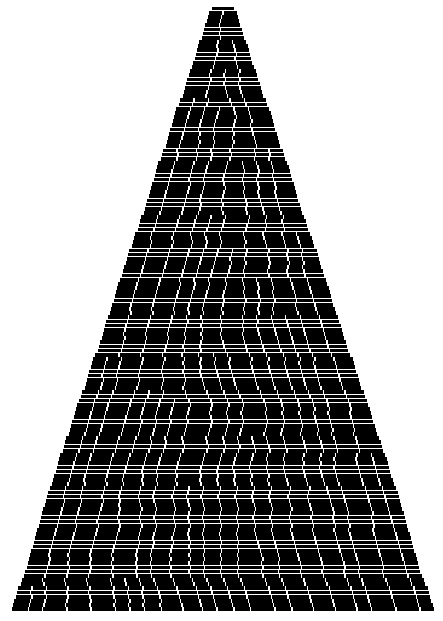
Здесь показано моделирование процесса вставок элементов со случайными ключами в первоначально пустое B-дерево со страницами, которые могут содержать девять ключей и ссылок. Каждая линия соответствует всем внешним узлам, а каждый отдельный узел изображается отрезком этой линии, длина которого пропорциональна количеству элементов в данном узле. Большинство вставок выполняется в незаполненных внешних узлах, что приводит к увеличению их размера на 1. Если вставка выполняется в заполненном внешнем узле, он разбивается на два узла половинного размера.

Рис. 16.9. Рост большого B-дерева с индикацией заполнения страниц

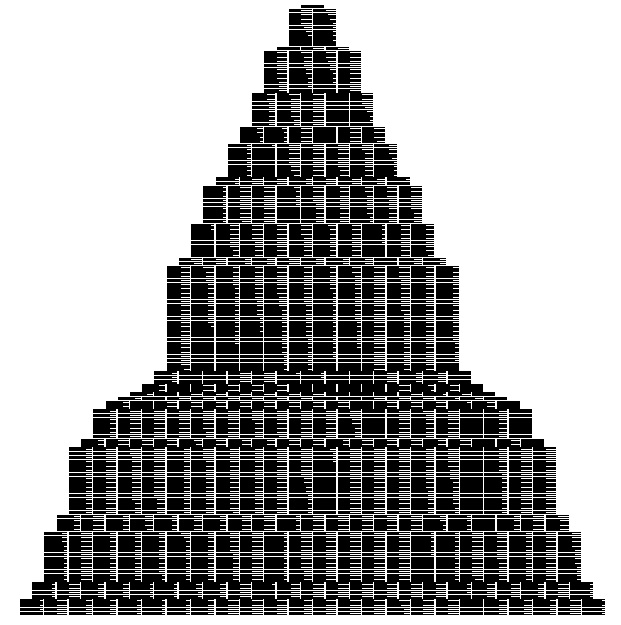
В этой версии рис. 16.8 показано заполнение страниц во время роста B-дерева. Как и в предыдущем случае, большинство вставок приходится на не заполненные страницы, лишь увеличивая их заполнение на 1. Когда вставка приходится на полную страницу, страница разбивается на две полупустые страницы.

В реальных ситуациях обычно можно использовать значительно более простой подход, оставляя внешние узлы незаполненными, что не особенно снижает производительность (см. упражнение 16.25).

Сразу же приходит на ум множество вариантов базовой абстракции B-дерева. Один класс вариантов позволяет экономить время за счет упаковки во внутренние узлы максимально возможного количества ссылок на страницы, в результате чего повышается коэффициент ветвления, и дерево становится более плоским. Как уже отмечалось, в современных системах преимущества, получаемые в результате таких изменений, несущественны, поскольку стандартные значения параметров позволяют реализовать операции найти и вставить всего за две пробы — такую эффективность вряд ли удастся повысить. Другой класс вариантов повышает эффективность использования дисковой памяти, объединяя перед разбиением узлы с их родственными узлами.

Упражнения 16.13—16.16 посвящены такому методу, который при работе со случайными ключами позволяет уменьшить излишние затраты дисковой памяти с 44 до 23%. Как обычно, выбор того или иного варианта зависит от свойств приложения. В силу наличия множества различных ситуаций, в которых применимы B-деревья, мы не будем подробно рассматривать эти вопросы. Мы не сможем также рассмотреть подробности реализаций, поскольку это потребовало бы учета слишком многих факторов, зависящих от устройств и систем. Как обычно, детальная разработка таких приложений — рискованное дело, и в современных системах желательно избегать наличия столь прихотливого и не переносимого кода, особенно если базовый алгоритм работает вполне успешно.

Упражнения

16.5. Приведите содержимое 3-4-5-6-дерева, образованного вставками ключей E A S Y Q U E S T I O N W I T H P L E N T Y O F K E Y S в указанном порядке в первоначально пустое дерево.

16.6. Постройте рисунки наподобие рис. 16.7, иллюстрирующие процесс вставки ключей 516, 177, 143, 632, 572, 161, 774, 470, 411, 706, 461, 612, 761, 474, 774, 635, 343, 461, 351, 430, 664, 127, 345, 171 и 357 в указанном порядке в первоначально пустое дерево при M= 5.

16.7. Приведите высоту B-деревьев, образованных вставками ключей из упражнения 16.6 в указанном порядке в первоначально пустое дерево для каждого значения M > 2.

16.8. Нарисуйте B-дерево, образованное вставками 16 одинаковых ключей в первоначально пустое дерево при M= 4.

16.9. Нарисуйте 1-2-дерево, образованное вставками ключей E A S Y Q U E S T I O N в первоначально пустое дерево. Объясните, почему 1-2-деревья не представляют практического интереса как сбалансированные деревья.

16.10. Измените реализацию вставки в B-дерево, приведенную в программе 16.3, чтобы разбиение в ней выполнялось при спуске вниз по дереву, аналогично реализации вставки в 2-3-4-дерево (программа 13.6).

16.11. Напишите программу для вычисления среднего количества внешних страниц B-дерева порядка M, построенного N случайными вставками в первоначально пустое дерево при использовании вероятностного процесса, описанного после леммы 16.1. Выполните программу для M= 10, 100 и 1000 и N= 10³, 10⁴, 10⁵ и 10⁶ .

16.12. Предположим, что в трехуровневом дереве а ссылок могут храниться во внутренней памяти, от b до 2b ссылок — в страницах, представляющих внутренние узлы, и от с до 2с элементов — в страницах, представляющих внешние узлы. Представьте максимальное количество элементов, которое может храниться в таком дереве, в виде функции от a, b и с.

16.13. Рассмотрите эвристику родственного разбиения B-деревьев (или B*-дерево): когда требуется разбить узел, содержащий M записей, мы объединяем этот узел с его родственным узлом. Если родственный узел содержит к записей, при к < M— 1, мы перераспределяем элементы, помещая и в родственный, и в полный узел приблизительно по (M + к)/2 записей. В противном случае мы создаем новый узел и помещаем в каждый узел дерева приблизительно по 2M/3 записей. Кроме того, мы позволяем корню расти до размера около 4M/3, разбивая его и создавая новый корневой узел с двумя записями, когда его размер достигает этого предельного значения. Укажите границы количества проб, используемых для выполнения поиска или вставки в B*-дереве порядка M, содержащем N элементов. Сравните эти границы с соответствующими границами для B-деревьев (см. лемму 16.2) при M= 10, 100 и 1000 и N= 10³, 10⁴, 10⁵ и 10⁶ .

16.14. Разработайте реализацию операции вставить для B*-дерева (основанную на

эвристике родственного разбиения) (см. упражнение 16.13).

16.15. Создайте рисунок, аналогичный рис. 16.8, для иллюстрации эвристики родственного разбиения (см. упражнение 16.13).

16.16. Выполните вероятностное моделирование (см. упражнение 16.11) для определения среднего количества страниц, задействованных при использовании эвристики родственного разбиения (см. упражнение 16.13) для построения B*-дерева порядка M вставками случайных узлов в первоначально пустое дерево, при M= 10, 100 и 1000 и N= 10³, 10⁴, 10⁵ и 10⁶ .

16.17. Напишите программу для восходящего построения индекса B-дерева, начиная с массива ссылок на страницы, содержащих от M до 2M упорядоченных элементов.

16.18. Можно ли построить индекс со всеми заполненными страницами, как на рис. 16.2, с помощью алгоритма вставки в B-дерево, рассмотренного в тексте (программа 16.3)? Обоснуйте свой ответ.

16.19. Предположим, что несколько различных компьютеров имеют доступ к одному и тому же индексу, и поэтому несколько программ практически одновременно могут попытаться вставить новый узел в одно и то же B-дерево. Объясните, почему в такой ситуации нисходящие B-деревья могут оказаться лучше восходящих. Считайте, что каждая программа может удержать (и удерживает) другие программы от модификации любого заданного узла, который она считала в память и может впоследствии изменить.

16.20. Измените реализацию B-дерева в программах 16.1—16.3, чтобы один узел дерева мог содержать M элементов.

16.21. Постройте таблицу значений разностей log999N и logi000N для N= 10³, 10⁴, 10⁵ и 10⁶ .

16.22. Реализуйте операцию сортировать для таблицы символов на основе B-дерева.

16.23. Реализуйте операцию выбрать для таблицы символов на основе B-дерева.

16.24. Реализуйте операцию удалить для таблицы символов на основе B-дерева.

16.25. Реализуйте операцию удалить для таблицы символов на основе B-дерева, используя простой метод, когда указанный элемент удаляется из внешней страницы (возможно, количество элементов в этой странице станет меньше M/2), но изменение не распространяется вверх по дереву, за исключением, возможно, коррекции значений ключей, если удаленный элемент был наименьшим в своей странице.

16.26. Измените программы 16.2 и 16.3, чтобы внутри узлов применялся бинарный поиск (см. программу 12.6). Определите значение M, которое минимизирует время, затрачиваемое программой на построение таблицы символов вставками N элементов со случайными ключами в первоначально пустую таблицу, при N= 10³, 10⁴, 10⁵ и 10⁶ . Сравните полученные значения времени с соответствующими значениями для RB-деревьев (программа 13.6).