|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Элементарные структуры данных
С помощью двух полей ссылок узлы можно связывать в два независимых списка: в один список по одному полю, и в другой - по другому. Здесь правое поле связывает узлы в одном порядке (например, в порядке их создания), а левое поле - в другом порядке (в нашем случае это порядок по возрастанию, возможно, в результате сортировки вставками, использующей только левое поле ссылки). Переходя по правым ссылкам от узла a, мы обойдем узлы в порядке их создания. Переходя по левым ссылкам от узла b, мы обойдем узлы в порядке возрастания.
При разработке алгоритмов для построения сложных структур данных часто применяют более одной ссылки для каждого узла - для эффективного управления ими. Например, список с двойными связями является мультисписком, который удовлетворяет ограничению: оба выражения x->l->r и x->r->l эквивалентны x. В "Рекурсия и деревья" рассматривается гораздо более важная структура данных с двумя ссылками для каждого узла.
Если многомерная матрица является разреженной (sparse) (количество ненулевых элементов относительно невелико), для ее представления вместо многомерного массива можно использовать мультисписок. Каждому значению матрицы соответствует один узел, а каждому измерению - по одной ссылке. Такие ссылки указывают на следующий элемент в своем измерении. Эта организация снижает объем необходимой памяти с произведения максимальных значений индексов измерений до пропорционального количеству ненулевых записей. Однако при этом для многих алгоритмов увеличивается время выполнения, поскольку для доступа к отдельным элементам приходится выполнять переходы по ссылкам.
Чтобы увидеть дополнительные примеры составных структур данных и четко понять различия между индексированными и связными структурами данных, рассмотрим структуры данных для представления графов. Граф (graph) - это фундаментальный комбинаторный объект, который определяется набором объектов (называемых вершинами) и набором связей между вершинами (называемых ребрами). Мы уже встречались с понятием графов в задаче связности из "Введение" .
Предположим, что граф с количеством вершин V и количеством ребер E описывается набором из E пар целых чисел в диапазоне от 0 до V-1. Это означает, что вершины обозначены целыми числами 0, 1, ..., V-1, а ребра определяются парами вершин. Как и в "Введение" , пара i-j обозначает связь между вершинами i и j и имеет то же значение, что и пара j-i. Графы, содержащие такие ребра, называются неориентированными (undirected). Другие типы графов рассматриваются в части 7.
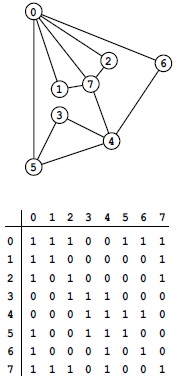
Один из простых методов представления графа заключается в использовании двумерного массива, называемого матрицей смежности (adjacency matrix). Она позволяет быстро определять, существует ли ребро между вершинами i и j, просто проверив на неравенство нулю элемент матрицы, находящийся на пересечении строки i и столбца j. Для неориентированных графов, которые мы сейчас рассматриваем, при наличии ненулевого элемента в строке i и столбце j ненулевым должен быть и элемент в строке j и столбце, т.е. матрица симметрична. На рис. 3.14 показан пример матрицы смежности для неориентированного графа.
Граф представляет собой набор вершин и соединяющих их ребер. Для простоты вершинам присвоены индексы (неотрицательные целые числа по порядку, начиная с нуля). Матрица смежности - это двумерный массив, содержащий бит 1 в строке i и столбце j в том и только том случае, когда между вершинами i и j существует ребро. Этот массив симметричен относительно диагонали. По соглашению все диагональные элементы содержат биты 1 (каждая вершина соединена сама с собой). Например, шестая строка (и шестой столбец) указывает, что вершина 6 соединена с вершинами 0, 4 и 6.
Программа 3.18 демонстрирует создание матрицы смежности для вводимой последовательности ребер.
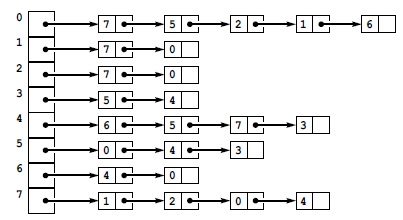
Другой простой метод представления графа предусматривает использование массива связанных списков, называемых списками смежности (adjacency lists). Каждой вершине соответствует связный список с узлами для всех вершин, связанных с данной. Для неориентированных графов должно выполняться следующее: если существует узел для вершины j в г-ом списке, то должен существовать и узел для вершины i в j-ом списке. На рис. 3.15 показан пример представления неориентированного графа с помощью списков смежности. В программе 3.19 приведен метод создания такого представления для вводимой последовательности ребер.
Программа 3.18. Представление графа в виде матрицы смежности
Эта программа выполняет чтение набора ребер, описывающих неориентированный граф, и создает для него представление в виде матрицы смежности. При этом элементам a[i][j] и a[j][i] присваивается значение 1, если существует ребро из i в j (или из j в j). Иначе эти элементы содержат значение 0. В программе предполагается, что количество вершин V - константа времени компиляции. Иначе пришлось бы динамически выделять память под массив, представляющий матрицу смежности (см. упражнение 3.71).
#include <iostream.h>
int main()
{ int i, j, adj[V][V];
for (i = 0; i < V; i++)
for (j = 0; j < V; j++) adj[i][j] = 0;
for (i = 0; i < V; i++) adj[i][i] = 1;
while (cin >> i >> j)
{ adj[i][j] = 1; adj[j][i] = 1; }
}
В этом представлении графа, изображенного на рис. 3.14, используется массив списков. Объем необходимой для данных памяти пропорционален сумме количеств вершин и ребер. Для поиска индексов вершин, связанных с данной вершиной i, анализируется i-я позиция массива, содержащая указатель на связный список, который содержит по одному узлу для каждой связанной с i вершины.
Программа 3.19. Представление графа в виде списков смежности
Эта программа считывает набор ребер, которые описывают граф, и создает его представление в виде списков смежности. Список смежности представляет собой массив списков, по одному для каждой вершины, где j-й список содержит связный список узлов, соединенных с j-ой вершиной.
#include <iostream.h>
struct node
{ int v; node* next;
node(int x, node* t)
{ v = x; next = t; }
};
typedef node *link;
int main()
{ int i, j; link adj[V];
for (i = 0; i < V; i++) adj[i] = 0;
while (cin >> i >> j)
{
adj[j] = new node(i, adj[j]);
adj[i] = new node(j, adj[i]);
}
}
Оба представления графа являются массивами более простых структур данных (по одной для каждой вершины), которые описывают ребра, связанные с данной вершиной. Для матрицы смежности более простая структура данных реализована в виде индексированного массива, а для списка смежности - в виде связного списка.
Таким образом, представления графа различными методами являются различными компромиссами между расходами памяти и времени. Для матрицы смежности необходим объем памяти, пропорциональный V2; для списков смежности объем памяти пропорционален V + E. При небольшом количестве ребер (такой граф называется разреженным), представление с использованием списков смежности потребует намного меньшего объема памяти. Если большинство пар вершин соединены ребрами (такой граф называется насыщенным), предпочтительнее использование матрицы смежности, поскольку в них не нужны ссылки. Некоторые алгоритмы более эффективны для представлений матрицей смежности, поскольку требуют постоянных затрат времени для ответа на вопрос "существует ли ребро между вершинами i и j?". Другие алгоритмы более эффективны для представлений списками смежности, поскольку они позволяют обрабатывать все ребра графа за время, пропорциональное V + E, а не V2. Конкретный пример такого выбора продемонстрирован в разделе 5.8 "Рекурсия и деревья" . Оба типа представлений можно элементарно распространить на другие типы графов (см., например, упражнение 3.70). Они служат основой большинства алгоритмов обработки графов, которые будут рассмотрены в части 7.
В завершение главы рассмотрим пример, демонстрирующий использование составных структур данных для эффективного решения простой геометрической задачи, о которой шла речь в разделе 3.2. Для данного значения d необходимо узнать количество пар из множества N точек внутри единичного квадрата, которые можно соединить отрезком прямой с длиной, меньшей d. В программе 3.20 используется двумерный массив связных списков, что снижает время выполнения по сравнению с программой 3.8 примерно на коэффициент 1/d2 для достаточно больших значений N. Для этого единичный квадрат разбивается на сетку меньших квадратов одинакового размера. Затем для каждого квадрата создается связный список всех точек, попадающих в квадрат. Двумерный массив обеспечивает непосредственный доступ к набору точек, ближайших к данной точке. Связные списки обладают гибкостью, позволяющей хранить все точки без необходимости знать заранее, сколько точек попадает в каждую ячейку сетки.
Объем используемой программой 3.20 памяти пропорционален 1/d2 + N , но время выполнения составляет O(d2 N2) , что существенно лучше грубой реализации из программы 3.8 при небольших значениях d. Например, для N = 106 и d = 0.001 затраты времени и памяти на решение задачи практически линейно зависят от N, в то время как грубый алгоритм требует неприемлемых затрат времени. Эту структуру данных можно использовать в качестве основы для решения многих других геометрических задач. Например, в сочетании с алгоритмом объединение-поиск из "Введение" она дает почти линейный алгоритм определения возможности соединения отрезками длиной d набора из N случайных точек на плоскости. Это фундаментальная задача из области проектирования сетей и цепей.
Программа 3.20. Двумерный массив списков
Эта программа демонстрирует эффективность правильного выбора структуры данных на примере геометрических вычислений из программы 3.8. Единичный квадрат разбивается на сетку. Создается двумерный массив связных списков, причем каждой ячейке (квадрату) сетки соответствует один список. Размер ячеек достаточно мал, чтобы все точки в пределах расстояния d от каждой данной точки попали в одну ячейку с ней либо в смежные ячейки. Функция malloc2d подобна одноименной функции из программы 3.16, но она создана для объектов типа link, а не int.
#include <math.h>
#include <iostream.h>
#include <stdlib.h>
#include "Point.h"
struct node
{ point p; node *next;
node(point pt, node* t) { p = pt; next = t; } }; typedef node *link;
static link **grid;
static int G, cnt = 0; static float d;
void gridinsert(float x, float y)
{ int X = x*G+1; int Y = y*G+1;
point p; p.x = x; p.y = y;
link s, t = new node(p, grid[X][Y]);
for (int i = X-1; i <= X+1; i++)
for (int j = Y-1; j <= Y+1; j++)
for (s = grid[i][j]; s != 0; s = s->next)
if (distance(s->p, t->p) < d) cnt+ + ;
grid[X][Y] = t;
}
int main(int argc, char *argv[])
{ int i, N = atoi(argv[1]);
d = atof(argv[2]); G = 1/d;
grid = malloc2d(G+2, G+2);
for (i = 0; i < G+2; i++)
for (int j = 0; j < G+2; j++)
grid[i][j] = 0;
for (i = 0; i < N; i++)
gridinsert(randFloat(), randFloat());
cout << cnt << " пар в радиусе " << d << endl;
}
Как следует из примеров этого раздела, данные различных типов можно объединять (косвенно, либо с помощью явных ссылок) в объекты, а последовательности объектов - в составные объекты. Таким образом из базовых абстрактных конструкций можно строить объекты неограниченной сложности. Хотя, как будет показано в "Рекурсия и деревья" , в этих примерах еще не достигнуто полное обобщение структурирования данных. Однако, прежде чем пройти последний этап, мы рассмотрим важные абстрактные структуры данных, которые можно создавать с помощью связных списков и массивов - основных средств достижения следующего уровня общности.
Упражнения
- 3.62. Напишите версию программы 3.16, обрабатывающую трехмерные массивы.
- 3.63. Измените программу 3.17 для индивидуальной обработки вводимых строк (память выделяется каждой строке после считывания ее из ввода). Можно предположить, что длина любой строки не превышает 100 символов.
- 3.64. Напишите программу заполнения двумерного массива значениями 0 или 1: элемент a[i][j] должен содержать значение 1, если наибольший общий делитель
- i и j равен единице, и значение 0 в остальных случаях.
- 3.65. Воспользуйтесь программами 3.20 и 1.4 для разработки эффективной программы, которая определяет, можно ли соединить набор из N точек отрезками длиной меньше d.
- 3.66. Напишите программу преобразования разреженной матрицы из двумерного массива в мультисписок с узлами только для ненулевых значений.
- 3.67. Реализуйте перемножение матриц, представленных мультисписками.
- 3.68. Запишите матрицу смежности, построенную программой 3.18, для введенных пар значений: 0-2, 1-4, 2-5, 3-6, 0-4, 6-0 и 1-3.
- 3.69. Запишите список смежности, построенный программой 3.19, для введенных пар значений: 0-2, 1-4, 2-5, 3-6, 0-4, 6-0 и 1-3.
- 3.70. Ориентированный (directed) граф - это граф, у которого связи между вершинами имеют направление: ребра следуют из одной вершины в другую. Выполните упражнения 3.68 и 3.69 для случая, когда вводимые пары представляют ориентированный граф, а обозначение i-j указывает, что ребро направлено из i в j. Кроме того, нарисуйте этот граф, используя стрелки для указания ориентации ребер.
- 3.71. Измените программу 3.18 таким образом, чтобы она принимала количество вершин в качестве аргумента командной строки, а затем динамически выделяла память под матрицу смежности.
- 3.72. Измените программу 3.19 таким образом, чтобы она принимала количество вершин в качестве аргумента командной строки, а затем динамически выделяла память под массив списков.
- 3.73. Напишите функцию, которая использует матрицу смежности графа для подсчета по заданным вершинам а и b количества таких вершин с, что существуют ребра из а в с и из с в b.
- 3.74. Выполните упражнение 3.73 с использованием списков смежности.