Массивы
module Array (
module Ix, - экспортирует весь Ix в целях удобства
Array, array, listArray, (!), bounds, indices, elems, assocs,
accumArray, (//), accum, ixmap ) where
import Ix
infixl 9 !, //
data (Ix a) => Array a b = ... - Абстрактный
array :: (Ix a) => (a,a) -> [(a,b)] -> Array a b
listArray :: (Ix a) => (a,a) -> [b] -> Array a b
(!) :: (Ix a) => Array a b -> a -> b
bounds :: (Ix a) => Array a b -> (a,a)
indices :: (Ix a) => Array a b -> [a]
elems :: (Ix a) => Array a b -> [b]
assocs :: (Ix a) => Array a b -> [(a,b)]
accumArray :: (Ix a) => (b -> c -> b) -> b -> (a,a) -> [(a,c)]
-> Array a b
(//) :: (Ix a) => Array a b -> [(a,b)] -> Array a b
accum :: (Ix a) => (b -> c -> b) -> Array a b -> [(a,c)]
-> Array a b
ixmap :: (Ix a, Ix b) => (a,a) -> (a -> b) -> Array b c
-> Array a c
instance Functor (Array a) where ...
instance (Ix a, Eq b) => Eq (Array a b) where ...
instance (Ix a, Ord b) => Ord (Array a b) where ...
instance (Ix a, Show a, Show b) => Show (Array a b) where ...
instance (Ix a, Read a, Read b) => Read (Array a b) where ...Haskell обеспечивает индексируемые массивы, которые можно рассматривать как функции, чьи области определения изоморфны соприкасающимся подмножествам целых чисел. Функции, ограниченные таким образом, можно эффективно реализовать; в частности, программист может ожидать разумно быстрого доступа к компонентам. Чтобы гарантировать возможность такой реализации, массивы обрабатываются как данные, а не как обычные функции.
Так как большинство функций массива затрагивают класс Ix, этот модуль экспортируется из Array, чтобы не было необходимости модулям импортировать и Array, и Ix.
16.1. Создание массивов
Если a -- тип индекса, а b -- любой тип, тип массивов с индексами в a и элементами в b записывается так: Array a b. Массив может быть создан с помощью функции array. Первым аргументом array является пара границ, каждая из которых имеет тип индекса массива. Эти границы являются соответственно наименьшим и наибольшим индексами в массиве. Например, вектор с началом в 1 длины 10 имеет границы (1,10), а матрица 10 на 10 с началом в 1 имеет границы ((1,1),(10,10)).
Вторым аргументом array является список ассоциаций вида (индекс, значение). Обычно этот список выражен в виде описания элементов. Ассоциация (i, x) определяет, что значением массива по индексу i является x. Массив не определен (т.е.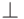 
), если какой-нибудь индекс в списке находится вне границ. Если какие-нибудь две ассоциации в списке имеют один и тот же индекс, значение по этому индексу не определено (т.е. 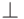). Так как индексы должны быть проверены на наличие этих ошибок, array является строгим по аргументу границ и по индексам списка ассоциаций, но не является строгим по значениям. Таким образом, возможны такие рекуррентные отношения:
a = array (1,100) ((1,1) : [(i, i * a!(i-1)) | i <- [2..100]])
Не каждый индекс в пределах границ массива обязан появиться в списке ассоциаций, но значения, связанные с индексами, которых нет в списке, будут не определены (т.е. 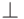). На примере 16.1 изображены некоторые примеры, которые используют конструктор array.
- Масштабирование массива чисел с помощью заданного числа:
scale :: (Num a, Ix b) => a -> Array b a -> Array b a
scale x a = array b [(i, a!i * x) | i <- range b]
where b = bounds a
- Инвертирование массива, который содержит перестановку своих индексов
invPerm :: (Ix a) => Array a a -> Array a a
invPerm a = array b [(a!i, i) | i <- range b]
where b = bounds a
- Скалярное произведение двух векторов
inner :: (Ix a, Num b) => Array a b -> Array a b -> b
inner v w = if b == bounds w
then sum [v!i * w!i | i <- range b]
else error "массивы не подходят для скалярного произведения"
where b = bounds v
Листинг
16.1.
Примеры массивов
Оператор (!) обозначает доступ к элементам массива по индексу (операция индексации массива). Функция bounds, будучи примененной к массиву, возвращает его границы. Функции indices, elems и assocs, будучи примененными к массиву, возвращают соответственно списки индексов, элементов или ассоциаций в порядке возрастания их индексов. Массив можно создать из пары границ и списка значений в порядке возрастания их индексов, используя функцию listArray.
Если в каком-либо измерении нижняя граница больше чем верхняя граница, то такой массив допустим, но он пуст. Индексация пустого массива всегда приводит к ошибке выхода за границы массива, но bounds по-прежнему сообщает границы, с которыми массив был создан.
16.1.1. Накопленные массивы
Другая функция создания массива, accumArray, ослабляет ограничение, при котором данный индекс может появляться не более одного раза в списке ассоциаций, используя функцию накопления, которая объединяет значения ассоциаций с одним и тем же индексом. Первым аргументом accumArray является функция накопления; вторым -- начальное значение; оставшиеся два аргумента являются соответственно парой границ и списком ассоциаций, как и для функции array. Например, при заданном списке значений некоторого типа индекса, hist создает гистограмму числа вхождений каждого индекса в пределах указанного диапазона:
hist :: (Ix a, Num b) => (a,a) -> [a] -> Array a b hist bnds is = accumArray (+) 0 bnds [(i, 1) | i <-is, inRange bnds i]
Если функция накопления является строгой, то accumArray является строгой в отношении значений, также как и в отношении индексов, в списке ассоциаций. Таким образом, в отличие от обычных массивов, накопленные массивы не должны быть в общем случае рекурсивными.
16.2. Добавочные обновления массивов
Оператор (//) принимает в качестве аргументов массив и список пар и возвращает массив, идентичный левому аргументу, за исключением того, что он обновлен ассоциациями из правого аргумента. (Как и с функцией array, индексы в списке ассоциаций должна быть уникальны по отношению к обновляемым элементам, которые определены.) Например, если m -- матрица n на n с началом в 1, то m//[((i,i), 0) | i <- [1..n]] -- та же самая матрица, у которой диагональ заполнена нулями.
accum f принимает в качестве аргументов массив и список ассоциаций и накапливает пары из списка в массив с помощью функции накопления f. Таким образом, accumArray можно определить через accum:
accumArray f z b = accum f (array b [(i, z) | i <- range b])
16.3. Производные массивы
Функции fmap и ixmap получают новые массивы из существующих; их можно рассматривать как обеспечение композиции функций слева и справа соответственно, с отображением, которое реализует исходный массив. Функция fmap преобразовывает значения массива, в то время как ixmap позволяет выполнять преобразования на индексах массива. На примере 16.2 изображены некоторые примеры.
- Прямоугольный подмассив
subArray :: (Ix a) => (a,a) -> Array a b -> Array a b
subArray bnds = ixmap bnds (\i->i)
- Строка матрицы
row :: (Ix a, Ix b) => a -> Array (a,b) c -> Array b c
row i x = ixmap (l',u') (\j->(i,j)) x where ((_,l'),(_,u')) = bounds x
- Диагональ матрицы (матрица предполагается квадратная)
diag :: (Ix a) => Array (a,a) b -> Array a b
diag x = ixmap (l,u) (\i->(i,i)) x
where
((l,_),(u,_)) = bounds x
- Проекция первых компонент массива пар
firstArray :: (Ix a) => Array a (b,c) -> Array a b
firstArray = fmap (\(x,y)->x)
Листинг
16.2.
Примеры производных массивов
16.4. Библиотека Array
module Array (
module Ix, - экспортировать весь Ix
Array, array, listArray, (!), bounds, indices, elems, assocs,
accumArray, (//), accum, ixmap ) where
import Ix
import List( (\\) )
infixl 9 !, //
data (Ix a) => Array a b = MkArray (a,a) (a -> b) deriving ()
array :: (Ix a) => (a,a) -> [(a,b)] -> Array a b
array b ivs =
if and [inRange b i | (i,_) <- ivs]
then MkArray b
(\j -> case [v | (i,v) <- ivs, i == j] of
[v] -> v
[] -> error "Array.!: \
\неопределенный элемент массива"
_ -> error "Array.!: \
\множественно определенный элемент массива")
else error "Array.array: ассоциация массива находится за пределами диапазона"
listArray :: (Ix a) => (a,a) -> [b] -> Array a b
listArray b vs = array b (zipWith (\ a b -> (a,b)) (range b) vs)
(!) :: (Ix a) => Array a b -> a -> b
(!) (MkArray _ f) = f
bounds :: (Ix a) => Array a b -> (a,a)
bounds (MkArray b _) = b
indices :: (Ix a) => Array a b -> [a]
indices = range . bounds
elems :: (Ix a) => Array a b -> [b]
elems a = [a!i | i <- indices a]
assocs :: (Ix a) => Array a b -> [(a,b)]
assocs a = [(i, a!i) | i <- indices a]
(//) :: (Ix a) => Array a b -> [(a,b)] -> Array a b
a // new_ivs = array (bounds a) (old_ivs ++ new_ivs)
where
old_ivs = [(i,a!i) | i <- indices a,
i `notElem` new_is]
new_is = [i | (i,_) <- new_ivs]
accum :: (Ix a) => (b -> c -> b) -> Array a b -> [(a,c)]
-> Array a b
accum f = foldl (\a (i,v) -> a // [(i,f (a!i) v)])
accumArray :: (Ix a) => (b -> c -> b) -> b -> (a,a) -> [(a,c)]
-> Array a b
accumArray f z b = accum f (array b [(i,z) | i <- range b])
ixmap :: (Ix a, Ix b) => (a,a) -> (a -> b) -> Array b c
-> Array a c
ixmap b f a = array b [(i, a ! f i) | i <- range b]
instance (Ix a) => Functor (Array a) where
fmap fn (MkArray b f) = MkArray b (fn . f)
instance (Ix a, Eq b) => Eq (Array a b) where
a == a' = assocs a == assocs a'
instance (Ix a, Ord b) => Ord (Array a b) where
a <= a' = assocs a <= assocs a'
instance (Ix a, Show a, Show b) => Show (Array a b) where
showsPrec p a = showParen (p > arrPrec) (
showString "array " .
showsPrec (arrPrec+1) (bounds a) . showChar ' ' .
showsPrec (arrPrec+1) (assocs a) )
instance (Ix a, Read a, Read b) => Read (Array a b) where
readsPrec p = readParen (p > arrPrec)
(\r -> [ (array b as, u)
| ("array",s) <- lex r,
(b,t) <- readsPrec (arrPrec+1) s,
(as,u) <- readsPrec (arrPrec+1) t ])
- Приоритет функции 'array' -- тот же, что и приоритет самого применения функции
arrPrec = 10