Спецификация производных экземпляров
Производный экземпляр представляет собой объявление экземпляра, которое генерируется автоматически в связи с объявлением data или newtype. Тело объявления производного экземпляра получается синтаксически из определения связанного с ним типа. Производные экземпляры возможны только для классов, известных компилятору: тех, которые определены или в Prelude, или в стандартной библиотеке. В этой лекции мы опишем выведение производных экземпляров классов, определенных в Prelude.
Если T - алгебраический тип данных, объявленный с помощью:
(где m <- 0 и круглые скобки можно опустить, если m=1 ), тогда объявление производного экземпляра возможно для класса C, если выполняются следующие условия:
- C является одним из классов Eq, Ord, Enum, Bounded, Show или Read.
- Есть контекст cx' такой, что cx' -> C tij выполняется для каждого из типов компонент tij.
- Если C является классом Bounded, тип должен быть перечислимым (все конструкторы должны быть с нулевым числом аргументов) или иметь только один конструктор.
- Если C является классом Enum, тип должен быть перечислимым.
- Не должно быть никакого явного объявления экземпляра где-либо в другом месте в программе, которое делает T u1 ... uk экземпляром C.
С целью выведения производных экземпляров, объявление newtype обрабатывается как объявление data с одним конструктором.
Если присутствует инструкция deriving, объявление экземпляра автоматически генерируется для T u1 ... uk по каждому классу Ci. Если объявление производного экземпляра невозможно для какого-либо из Ci, то возникнет статическая ошибка. Если производные экземпляры не требуются, инструкцию deriving можно опустить или можно использовать инструкцию deriving ().
Каждое объявление производного экземпляра будет иметь вид:
instance (cx, cx') => Ci (T u1 ... uk) where { d }где d выводится автоматически в зависимости от Ci и объявления типа данных для T (как будет описано в оставшейся части этого раздела).
Контекст cx' является самым маленьким контекстом, удовлетворяющим приведенному выше пункту (2). Для взаимно рекурсивных типов данных компилятор может потребовать выполнения вычисления с фиксированной точкой, чтобы его вычислить.
Теперь дадим оставшиеся детали производных экземпляров для каждого из выводимых классов Prelude. Свободные переменные и конструкторы, используемые в этих трансляциях, всегда ссылаются на объекты, определенные в Prelude.
10.1. Производные экземпляры классов Eq и Ord
Производные экземпляры классов Eq и Ord автоматически вводят методы класса (==), (/=), compare, (<), (<-), (>), (->), max и min. Последние семь операторов определены так, чтобы сравнивать свои аргументы лексикографически по отношению к заданному набору конструкторов: чем раньше стоит конструктор в объявлении типа данных, тем меньше он считается по сравнению с более поздними. Например, для типа данных Bool мы получим: (True > False) == True.
Выведенные сравнения всегда обходят конструкторы слева направо. Приведенные ниже примеры иллюстрируют это свойство:
(1,undefined) == (2,undefined) => False (undefined,1) == (undefined,2) => _|_
Все выведенные операции классов Eq и Ord являются строгими в отношении обоих аргументов. Например, False <- ? является 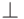 , даже если False является первым конструктором типа Bool.
, даже если False является первым конструктором типа Bool.
10.2. Производные экземпляры класса Enum
Объявления производных экземпляров класса Enum возможны только для перечислений (типов данных с конструкторами, которые имеют только нулевое число аргументов).
Конструкторы с нулевым числом аргументов считаются пронумерованными слева направо индексами от 0 до n-1. Операторы succ и pred дают соответственно предыдущее и последующее значение в соответствии с этой схемой нумерации. Будет ошибкой применить succ к максимальному элементу или pred - к минимальному элементу.
Операторы toEnum и fromEnum отображают перечислимые значения в значения типа Int и обратно; toEnum вызывает ошибку времени выполнения программы, если аргумент Int не является индексом одного из конструкторов.
Определения оставшихся методов:
enumFrom x = enumFromTo x lastCon
enumFromThen x y = enumFromThenTo x y bound
where
bound | fromEnum y >= fromEnum x = lastCon
| otherwise = firstCon
enumFromTo x y = map toEnum [fromEnum x .. fromEnum y]
enumFromThenTo x y z = map toEnum [fromEnum x, fromEnum y .. fromEnum z]где firstCon и lastCon - соответственно первый и последний конструкторы, перечисленные в объявлении data. Например, с учетом типа данных:
data Color = Red | Orange | Yellow | Green deriving (Enum)
мы имели бы:
[Orange ..] == [Orange, Yellow, Green] fromEnum Yellow == 2
10.3. Производные экземпляры класса Bounded
Класс Bounded вводит методы класса minBound и maxBound, которые определяют минимальный и максимальный элемент типа. Для перечисления границами являются первый и последний конструкторы, перечисленные в объявлении data. Для типа с одним конструктором конструктор применяется к границам типов компонент. Например, следующий тип данных:
data Pair a b = Pair a b deriving Bounded
произвел бы следующий экземпляр класса Bounded:
instance (Bounded a,Bounded b) => Bounded (Pair a b) where
minBound = Pair minBound minBound
maxBound = Pair maxBound maxBound10.4. Производные экземпляры классов Read и Show
Производные экземпляры классов Read и Show автоматически вводят методы класса showsPrec, readsPrec, showList и readList. Они используются для перевода значений в строки и перевода строк в значения.
Функция showsPrec d x r принимает в качестве аргументов уровень приоритета d (число от 0 до 11), значение x и строку r. Она возвращает строковое представление x, соединенное с r. showsPrec удовлетворяет правилу:
showsPrec d x r ++ s == showsPrec d x (r ++ s)
Представление будет заключено в круглые скобки, если приоритет конструктора верхнего уровня в x меньше чем d. Таким образом, если d равно 0, то результат никогда не будет заключен в круглые скобки; если d равно 11, то он всегда будет заключен в круглые скобки, если он не является атомарным выражением (вспомним, что применение функции имеет приоритет 10). Дополнительный параметр r необходим, если древовидные структуры должны быть напечатаны за линейное, а не квадратичное время от размера дерева.
Функция readsPrec d s принимает в качестве аргументов уровень приоритета d (число от 0 до 10) и строку s и пытается выполнить разбор значения в начале строки, возвращая список пар (разобранное значение, оставшаяся часть строки). Если нет успешного разбора, возвращаемый список пуст. Разбор инфиксного оператора, который не заключен в круглые скобки, завершится успешно, только если приоритет оператора больше чем или равен d.
Должно выполняться следующее:
(x,"") должен являться элементом (readsPrec d (showsPrec d x ""))
То есть readsPrec должен уметь выполнять разбор строки, полученной с помощью showsPrec, и должен передавать значение, с которого showsPrec начал работу.
showList и readList позволяют получить представление списков объектов, используя нестандартные обозначения. Это особенно полезно для строк (списков Char ).
readsPrec выполняет разбор любого допустимого представления стандартных типов, кроме строк, для которых допустимы только строки, заключенные в кавычки, и других списков, для которых допустим только вид в квадратных скобках [...]. См. лекцию "8" для получения исчерпывающих подробностей.
Результат show представляет собой синтаксически правильное выражение Haskell , содержащее только константы, с учетом находящихся в силе infix-объявлений в месте, где объявлен тип. Он содержит только имена конструкторов, определенных в типе данных, круглые скобки и пробелы. Когда используются именованные поля конструктора, также используются фигурные скобки, запятые, имена полей и знаки равенства. Круглые скобки добавляются только там, где это необходимо, игнорируя ассоциативность. Никакие разрывы строк не добавляются. Результат show может быть прочитан с помощью read, если все типы компонент могут быть прочитаны. (Это выполняется для экземпляров, определенных в Prelude, но может не выполняться для определяемых пользователем экземпляров.)
Производные экземпляры класса Read делают следующие предположения, которым подчиняются производные экземпляры класса Show:
- Если конструктор определен как инфиксный оператор, то выведенный экземпляр класса Read будет разбирать только инфиксные применения конструктора (не префиксную форму).
- Ассоциативность не используется для того, чтобы уменьшить появление круглых скобок, хотя приоритет может быть. Например, с учетом
infixr 4 :$ data T = Int :$ T | NT
получим:
- show (1 :$ 2 :$ NT) породит строку "1 :$ (2 :$ NT)".
- read "1 :$ (2 :$ NT)" завершится успешно с очевидным результатом.
- read "1 :$ 2 :$ NT" завершится неуспешно.
- Если конструктор определен с использованием синтаксиса записей, выведенный экземпляр Read будет выполнять разбор только форм синтаксиса записей, и более того, поля должны быть заданы в том же порядке, что и в исходном объявлении.
- Производный экземпляр Read допускает произвольные пробельные символы Haskell между токенами входной строки. Дополнительные круглые скобки также разрешены.
Производные экземпляры Read и Show могут не подходить для некоторых использований. Среди таких проблем есть следующие:
- Круговые структуры не могут быть напечатаны или считаны с помощью этих экземпляров.
- При распечатывании структур теряется их общая основа; напечатанное представление объекта может оказаться намного больше, чем это необходимо.
- Методы разбора, используемые при считывании, очень неэффективны; считывание большой структуры может оказаться весьма медленным.
- Нет никакого пользовательского контроля над распечатыванием типов, определенных в Prelude. Например, нет никакого способа изменить форматирование чисел с плавающей точкой.
10.5. Пример
В качестве законченного примера рассмотрим тип данных дерево:
data Tree a = Leaf a | Tree a :^: Tree a
deriving (Eq, Ord, Read, Show)Автоматическое выведение объявлений экземпляров для Bounded и Enum невозможны, поскольку Tree не является перечислением и не является типом данных с одним конструктором. Полные объявления экземпляров для Tree приведены на рис. 10.1. Обратите внимание на неявное использование заданных по умолчанию определений методов классов - например, только  определен для Ord, тогда как другие методы класса (<, >, >=, max и min), определенные по умолчанию, заданы в объявлении класса, приведенном на рис. 6.1.
определен для Ord, тогда как другие методы класса (<, >, >=, max и min), определенные по умолчанию, заданы в объявлении класса, приведенном на рис. 6.1.
infixr 5 :^:
data Tree a = Leaf a | Tree a :^: Tree a
instance (Eq a) => Eq (Tree a) where
Leaf m == Leaf n = m==n
u:^:v == x:^:y = u==x && v==y
_ == _ = False
instance (Ord a) => Ord (Tree a) where
Leaf m <= Leaf n = m<=n
Leaf m <= x:^:y = True
u:^:v <= Leaf n = False
u:^:v <= x:^:y = u<x || u==x && v<=y
instance (Show a) => Show (Tree a) where
showsPrec d (Leaf m) = showParen (d > app_prec) showStr
where
showStr = showString "Лист " . showsPrec (app_prec+1) m
showsPrec d (u :^: v) = showParen (d > up_prec) showStr
where
showStr = showsPrec (up_prec+1) u .
showString " :^: " .
showsPrec (up_prec+1) v
- Обратите внимание: правоассоциативность :^: игнорируется
instance (Read a) => Read (Tree a) where
readsPrec d r = readParen (d > up_prec)
(\r -> [(u:^:v,w) |
(u,s) <- readsPrec (up_prec+1) r,
(":^:",t) <- lex s,
(v,w) <- readsPrec (up_prec+1) t]) r
++ readParen (d > app_prec)
(\r -> [(Leaf m,t) |
("Лист",s) <- lex r,
(m,t) <- readsPrec (app_prec+1) s]) r
up_prec = 5 - Приоритет :^:
app_prec = 10 - Применение имеет приоритет на единицу больше чем
- наиболее сильно связанный оператор
Листинг
10.1.
Пример производных экземпляров
