Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 8:

Методы расщепления
A
|
версия для печати
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

8.2.2. Схемы Кранка - Никольсон

Рассмотрим обобщение схемы Кранка - Никольсон на случай многомерных уравнений с локально - одномерными операторами. Положим, как и ранее, 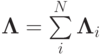{\mathbf{\Lambda}} = \sum\limits_i^{N}{{\mathbf{\Lambda}}_i }. Если коэффициенты разностного оператора явно зависят от времени, они берутся на промежуточном временном слое 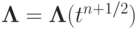{\mathbf{\Lambda}} = {\mathbf{\Lambda}}(t^{{n} + 1/2} ). Для простоты изложения рассмотрим двумерный случай.

Схему расщепления по направлениям представим в виде

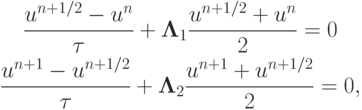
\begin{gather*} \frac{{u^{{n} + 1/2} - u^{n}}}{\tau} + {\mathbf{\Lambda}}_1 \frac{{u^{{n} + 1/2} + u^{n}}}{2} = 0 \\ \frac{{u^{{n} + 1} - u^{{n} + 1/2}}}{\tau} + {\mathbf{\Lambda}}_2 \frac{{u^{{n} + 1} + u^{{n} + 1/2}}}{2} = 0, \end{gather*}

а решение на следующем слое по времени в операторной форме выписывается как 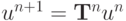u^{{n} + 1} = {\mathbf{T}}^{n} u^{n}. Для оператора послойного перехода получается следующая формула:

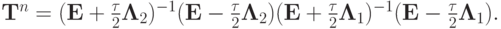
$ {\mathbf{T}}^{n} = ({\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_2 )^{- 1} ({\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_2)({\mathbf{E}} + \frac{\tau}{2}{\mathbf{\Lambda}}_1 )^{- 1} ({\mathbf{E}} - \frac{\tau}{2}{\mathbf{\Lambda}}_1). $

При выполнении условия

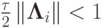
$ \frac{\tau}{2} \left\|{{\mathbf{\Lambda}}_i }\right\| < 1 $

схема устойчива, обладает вторым порядком аппроксимации по времени, если операторы 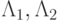\Lambda _{1}, \Lambda _{2} коммутативны, и первым — если нет.

8.2.3. Общая формулировка методов расщепления

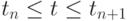Заменим локально - одномерные дифференциальные операторы \mathbf{A}_i разностными операторами на каждом шаге по времени t_n \le t \le t_{{n} + 1}. Представим схему расщепления в следующем общем виде:

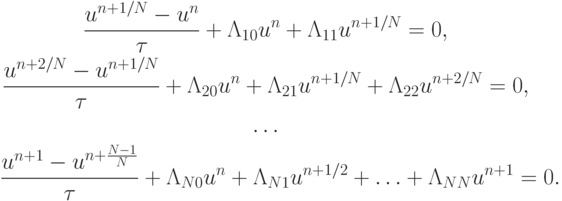
\begin{gather*} \frac{{u^{{n} + 1/{N}} - u^{n}}}{\tau} + {{{\Lambda}}}_{10}u^{n} + {{{\Lambda}}}_{11} u^{{n} + 1/{N}} = 0, \\ \frac{{u^{{n} + 2/{N}} - u^{{n} + 1/{N}}}}{\tau } + {{{\Lambda}}}_{20} u^{n} + {{{\Lambda}}}_{21} u^{{n} + 1/{N}} + {{{\Lambda}}}_{22} u^{{n} + 2/{N}} = 0, \\ \ldots \\ \frac{u^{n + 1} - u^{n + \frac{N - 1}{N}}}{\tau} + {{{\Lambda}}}_{{N}0} u^{n} + {{{\Lambda}}}_{{N}1} u^{{n} + 1/2} + \ldots + {{{\Lambda}}}_{{N}{N}} u^{{n} + 1} = 0. \end{gather*}

Условие устойчивости такой схемы расщепления будет

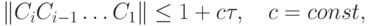
\left\|{C_i C_{{i} - 1} \ldots C_1}\right\| \le 1 + c {\tau}, \quad c = const,

где 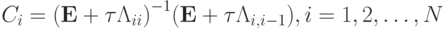C_i = {(\mathbf{E} + {\tau}\Lambda_{ii})}^{- 1} (\mathbf{E} + \tau \Lambda_{i, i - 1}), i = 1, 2, \ldots , N Двухслойная схема расщепления с весовыми коэффициентами представлена в виде

\begin{gather*} \frac{{u^{{n} + 1/{N}} - u^{n}}}{\tau} + {\mathbf{\Lambda}}_1 \left[{(1 - {\sigma})u^{n} + {\sigma}u^{{n} + 1/{N}}}\right] = 0, \\ \frac{{u^{{n} + 2/{N}} - u^{{n} + 1/{N}}}}{\tau } + {\mathbf{\Lambda}}_2 \left[{(1 - \sigma )u^{{n} + 1/{N}} + \sigma u^{{n} + 2/{N}}}\right] = 0, \\ \ldots \\ \frac{{u^{{n} + 1} - u^{{n} + \frac{{{N} - 1}}{{N}}}}}{\tau} + {\mathbf{\Lambda}}_n \left[ {(1 - {\sigma})u^{{n} + \frac{{{N} - 1}}{{N}}} + {\sigma}u^{{n} + 1}}\right] = 0. \end{gather*}

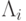Если в этой схеме расщепления положить веса верхнего и нижнего слоев по времени равными, \gamma = 0, 5, то в случае коммутирующих операторов \Lambda _{i} (каждый такой разностный оператор аппроксимирует со вторым порядком соответствующий локально - одномерный дифференциальный оператор) схема будет иметь второй порядок аппроксимации и по времени. Если при этом каждый оператор 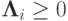{\mathbf{\Lambda}}_i \ge 0, то схема будет абсолютно устойчивой.

8.2.4. Схемы расщепления для уравнения теплопроводности

Рассматриваем нестационарное уравнение теплопроводности

$ \frac{{\partial}u}{{\partial}t} - \Delta u = 0, t \in \Omega_t , \left\{{x, y, z}\right\} \in \Omega . $

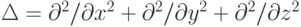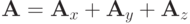Здесь оператор Лапласа определен как \Delta = {\partial}^2 / {\partial}x^2 + {\partial}^2 / {\partial}y^2 + {\partial}^2 / {\partial}z^2. Его также можно записать в виде суммы трех локально - одномерных операторов \mathbf{A} = \mathbf{A}_x + \mathbf{A}_y + \mathbf{A}_{z}. Соответствующие разностные операторы будут 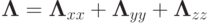{\mathbf{\Lambda}} = {\mathbf{\Lambda}}_{xx} + {\mathbf{\Lambda}}_{yy} + {\mathbf{\Lambda}}_{zz}, где

$ \Lambda_{xx} = \frac{u_{m - 1, jk} - 2u_{mjk} + u_{m + 1, jk}}{h_x^2} $
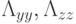аналогично определяются операторы вычисления второй разностной производной и по остальным направлениям \Lambda _{yy}, \Lambda _{zz} Локально - одномерная схема для уравнения теплопроводности будет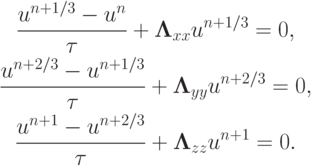

\begin{gather*} \frac{{u^{{n} + 1/3} - u^{n}}}{\tau} + {\mathbf{\Lambda}}_{xx}u^{{n} + 1/3} = 0, \\ \frac{{u^{n + 2/3} - u^{{n} + 1/3}}}{\tau} + {\mathbf{\Lambda}}_{yy}u^{{n} + 2/3} = 0, \\ \frac{{u^{{n} + 1} - u^{{n} + 2/3}}}{\tau} + {\mathbf{\Lambda}}_{zz}u^{{n} + 1} = 0. \end{gather*}

Для повышения порядка аппроксимации можно использовать схему с весами

\begin{gather*} \frac{{u^{{n} + 1/3} - u^{n}}}{\tau } + {\mathbf{\Lambda}}_{xx} \left[{(1 - {\sigma})u^n + {\sigma}u^{n + 1/3}}\right] = 0, \\ \frac{{u^{{n} + 2/3} - u^{{n} + 1/3}}}{\tau} + {\mathbf{\Lambda}}_{yy} \left[{(1 - {\sigma})u^{{n} + 1/3} + {\sigma}u^{{n} + 2/3}}\right] = 0, \\ \frac{{u^{{n} + 1} - u^{{n} + 2/3}}}{\tau} + {\mathbf{\Lambda}}_{zz}[(1 - {\sigma})u^{{n} + 2/3} + {\sigma}u^{{n} + 1} ] = 0. \end{gather*}
Дальше >>
< Лекция 7 || Лекция 8: 123456 || Лекция 9 >

Вопросы и ответы

вопросов: 0