Введение в методы численного решения уравнений газовой динамики
4.6. Задачи для самостоятельного решения
-
Волны Римана
Выпишем нелинейную систему уравнений одномерных движений идеальной сжимаемой жидкости в случае баротропных процессов. Она состоит из уравнения Эйлера
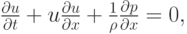
уравнения неразрывности

и условия баротропности
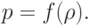
Уравнения позволяют определить плотность
 и скорость u в зависимости от координаты x и времени t. Система не имеет решений, зависящих только от
и скорость u в зависимости от координаты x и времени t. Система не имеет решений, зависящих только от 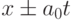 , но оказывается возможным найти решение этой системы, представляющее собой плоскую волну и являющееся обобщением решений вида
, но оказывается возможным найти решение этой системы, представляющее собой плоскую волну и являющееся обобщением решений вида  . Будем искать такие решения системы, для которых скорость u является функцией только плотности
. Будем искать такие решения системы, для которых скорость u является функцией только плотности 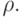 Частные решения системы уравнений носят названия решений Римана; соответствующие этим решениям движения называются волнами Римана
Частные решения системы уравнений носят названия решений Римана; соответствующие этим решениям движения называются волнами Римана  .
.- Доказать, что в рассматриваемом течении скорость можно определить по формуле

Обозначим
и введем величину c = u + a. Какой физический смысл имеет величина c?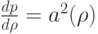
- Задав начальный профиль возмущения плотности, численно решить уравнение для
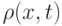 :
:
- для случая адиабатических движений совершенного газа (
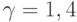 ):
):![$ c \left({\rho}\right) = \sqrt {A \gamma } \left[{1 +
\frac{2}{{\gamma - 1}}}\right] {\rho}^{{{1 \over 2}}(\gamma - 1)}, $](/sites/default/files/tex_cache/477a818ffac74ef98fa8088549590118.png)
- задав самостоятельно некоторую зависимость давления от плотности,
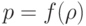 .
.
- для случая адиабатических движений совершенного газа (
- Описать качественное поведение решения
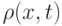 . Указать, какие требования к численному методу предъявляет возникновение в потоке скачков уплотнения. Вывести зависимость
. Указать, какие требования к численному методу предъявляет возникновение в потоке скачков уплотнения. Вывести зависимость 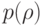 , при которой не возникает эффекта опрокидывания волны сжатия Римана. Дать физическую трактовку полученного
соотношения. Провести численный расчет течения с полученной зависимостью
, при которой не возникает эффекта опрокидывания волны сжатия Римана. Дать физическую трактовку полученного
соотношения. Провести численный расчет течения с полученной зависимостью 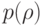 .
. - Доказать, что рассмотренные решения Римана можно определить как такие решения, для которых имеется семейство прямолинейных характеристик.
- Поставить условия существования центрированных волн Римана, когда
 .
.Течения подобного типа — частный случай автомодельных течений, когда решение зависит от некоторой комбинации независимых переменных. Проиллюстрировать численными расчетами особенности распространения центрированных волн Римана.
- Доказать, что в рассматриваемом течении скорость можно определить по формуле
