Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 4:

Введение в методы численного решения уравнений газовой динамики
A
|
версия для печати
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

теперь имеется алгоритм вычисления 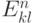E_{kl}^{n} и, следовательно, \tilde {E}_{kl}^{n}.

Из соотношения

$ \bar{e}_{kl} \cdot h^2 = (h^2 \rho_{kl} ) \bar{\varepsilon}_{kl} + (h^2 \rho_{kl} ) \cdot \frac{{(\bar{u}_{1, {kl}} )^2 + (\bar{u}_{2, {kl}} )^2}}{2} $

находим величину полной удельной внутренней энергии \bar{\varepsilon}_{kl}. Однако искомыми являются значения удельной внутренней энергии для каждого вещества. Пусть \Delta \varepsilon _{i} — изменение удельной внутренней энергии i вещества за первый этап шага по времени по i веществу. Зная mi (масса i вещества), запишем полное приращение полной удельной внутренней энергии в ячейке ( \Delta _{\varepsilon } ) и приравняем его к уже полученному полному приращению

\sum\limits_i {m_{ikl}^{n}} \Delta \varepsilon_{ikl} = m_{kl}^{n} (\bar{\varepsilon}_{kl} - \varepsilon_{kl}^{n}).

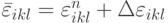Для определения изменения количества каждого газа нужно сделать некое правдоподобное предположение, например, считать, что все \Delta \varepsilon _{ikl} одинаковы. Тогда {N} \Delta \varepsilon_{ikl} = \bar{\varepsilon}_{kl}^{n} - \varepsilon_{kl}^{n} и, соответственно, \bar{\varepsilon}_{ikl} = \varepsilon_{ikl}^{n} + \Delta \varepsilon_{ikl}. На этом первый этап расчета (предиктор) закончен.

Рассмотрим второй этап расчета.

Движение частиц описывается обыкновенными дифференциальными уравнениями

$ \dot{X}_p = u_1({t, X}_p, Y_p), \dot{Y}_p = u_2({t, X}_p, Y_p), $

которые могут быть приближены, например, с использованием явного метода Эйлера. Тогда дифференциальные уравнения заменяются разностными уравнениями

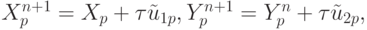
X_p^{{n} + 1} = X_p + {\tau}\tilde{u}_{1 p}, Y_p^{{n} + 1} = Y_p^{n} + {\tau}\tilde{u}_{2 p},

где скорости частиц $ \tilde{u}_k, \tilde{v}_k $ определяются интерполяцией величин $ \bar{u}_{1}, \bar{u}_{2} $ в ячейках, окружающих p частицу.

После этого рассчитывается перенос массы и вычисляется новая масса каждой ячейки. Для этого выделяются три группы частиц:

  • частицы, оставшиеся при переходе на n + 1 слой в пределах ячейки, которые, очевидно, не вносят изменений в массу, импульс, энергию новой ячейки, т.е.
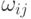    (X_p^{n}, Y_p^{n}) \in \omega_{ij}, (X_p^{n + 1}, Y_p^{n + 1}) \in \omega_{ij},
    где \omega _{ij} — обозначение старой ячейки,
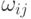  • частицы, покинувшие ячейку \omega _{ij}:
    (X_p^{n}, Y_p^{n}) \in \omega_{ij}, \\ (X_p^{n + 1}, Y_p^{n + 1}) \notin \omega_{ij},
  • частицы, перешедшие из соседних ячеек:
    (X_p^{n}, Y_p^{n}) \notin \omega_{ij}, \\ {(X_p^{n + 1}, Y_p^{n + 1}) \in \omega_{ij}, }

На шаг по времени накладывается ограничение

$ {\tau} < \frac{h}{{\sqrt {u_1^2 + u_2^2}}}, $

что означает запрет на перемещение частицы за один шаг больше, чем на одну ячейку. Перемещение в данном методе возможно только в соседнюю ячейку. Предположим, что каждая p частица, перешедшая на n + 1 шаге по времени в соседнюю ячейку, переносит в нее массу mp. Это означает, что значение массы mikl считается путем сложения масс всех частиц типа i, для которых (X_p^{n + 1}, Y_p^{n + 1}) \in \omega_{ij}

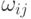Процедура вычисления импульса выполняется следующим образом. Компоненты полного импульса частиц в ячейке ( k, l ) могут быть вычислены, как m_{kl}^{n} \overline{u}_{1, kl}, m_{kl}^{n} \overline{u}_{2, kl}, при этом p частица, покинувшая ячейку \omega _{ij}, уносит импульс m_p \overline{u}_{1, {kl}}, m_p u_{2, kl}. Изменение импульса в Skl за один шаг по времени будет

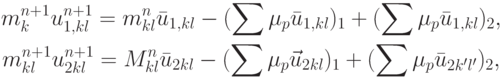
\begin{gather*} m_k^{{n} + 1} u_{1, {kl}}^{{n} + 1} = m_{kl}^{n} \bar{u}_{1, {kl}} - (\sum {\mu_p \bar{u}_{1, {kl}}} )_1 + (\sum {\mu_p \bar{u}_{1, {kl}}} )_2 , \\ m_{kl}^{{n} + 1} u_{2 {kl}}^{{n} + 1} = M_{kl}^{n} \bar{u}_{2 {kl}} - (\sum {\mu_p \vec{u}_{2 {kl}}} )_1 + (\sum {\mu_p \bar{u}_{2 k^{\prime}l^{\prime}}} )_2 , \end{gather*}

здесь символы суммирования означают суммирование по частицам ( p ), покинувшим данную ячейку и пришедшим в нее, соответственно. После вычисления компонентов импульса каждой ячейки вычисляются компоненты скорости u_{1kl}^{n + 1}, u_{2kl}^{n + 1}.

Частица типа i, переходящая из Ske в другую ячейку, переносит полную энергию

$ \Delta E_p = m_p \left[{\bar{\varepsilon}_{ikl} + \frac{{(\bar{u}_{1 {kl}} )^2 + (\bar u_{2 {kl}} )^2}}{2}}\right]. $

Тогда можно вычислить энергию i вещества в ячейке \omega _{kl} на промежуточном шаге:

$ E_{ikl} = \sum\limits_{i_p \in i}{m_p } \left[{\bar{\varepsilon }_{ikl} + \frac{{(\bar{u}_{1 {kl}} )^2 + (\bar{u}_{2 {kl}} )^2}}{2}}\right]. $

При t = tn + 1 полная удельная энергия изменится на величину

E_{ikl}^{n + 1} = \bar{E}_{ikl} - (\sum\limits_{i_p \in i}{\cdot \Delta E_p } )_1 + (\sum\limits_{i_p \in i}{\cdot \Delta E_p } )_2,

где знаки суммирования снова означают суммы по всем частицам, покинувшим ячейку \omega _{kl} и пришедшим в нее, соответственно. Далее получим

$ \varepsilon_{ikl}^{n + 1} = \frac{{h^2}}{{m_{ikl}^{n + 1}}}E_{ikl}^{n + 1} - \frac{1}{2} \left[{(u_{1 {kl}}^{n + 1} )^2 + (u_{2 {kl}}^{n + 1} )^2}\right]. $

Отметим недостатки этого метода. Во - первых, это дискретность плотности, что приводит при небольшом количестве частиц в ячейке к скачкообразным изменениям плотности. Во - вторых, аппроксимация исходных уравнений достигается при количестве частиц, стремящемся к бесконечности. Кроме того, этот метод требует значительно большего количества памяти, чем конечно - разностные методы, так как наряду с физическими характеристиками узлов необходимо хранить и свойства частиц в ячейках.

Подробное описание метода частиц в ячейках в [14.11].

Дальше >>
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

Вопросы и ответы

вопросов: 0