Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности
-
Тепловой кристалл
Рассмотрим уравнение
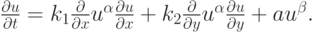
Попытайтесь качественно исследовать свойства решений этого уравнения.
В случае
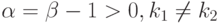 рассмотреть задачу со
следующими граничными условиями:
рассмотреть задачу со
следующими граничными условиями: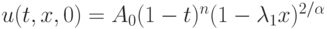
при
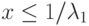 ,
,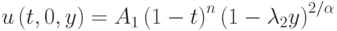
при
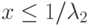 , иначе 0. Здесь n < 0 — действительное число.
, иначе 0. Здесь n < 0 — действительное число.Рассмотреть случаи
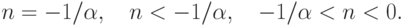
Решить задачу численно и сравнить полученное решение с аналитическим. Решение тепловой кристалл описано в [12.4, c. 148 - 155].
-
Остановка тепловой волны
Модифицируем задачу 6:

( 2.11) положив
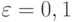 .
.- Выполнить пункты задачи 6. Как влияет малый линейный сток на поведение решения?
- В случае
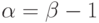 найти автомодельное решение,
аналогичное рассматриваемому в задаче (7).
найти автомодельное решение,
аналогичное рассматриваемому в задаче (7).Указание. Рассмотреть последовательность замен
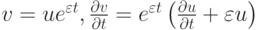
и
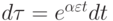 .
.Каким станет уравнение (2.11) в переменных v, x, t?
- Рассмотреть задачу о формировании теплового кристалла для уравнения (2.11).
-
Неустойчивость Тьюринга
Рассмотрим систему
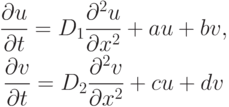
с условиями
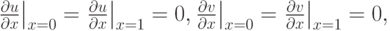
причем a + d < 0, ad - bc > 0. При этих условиях особая точка (0, 0) системы
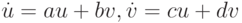 устойчива. Пусть, без ограничения общности, a > 0.
устойчива. Пусть, без ограничения общности, a > 0.- Найти условие, когда внесение в систему диффузии приводит к потере устойчивости однородного стационарного решения.
Указание. Рассмотреть преобразование Фурье по пространственной переменной. Исследовать на устойчивость особые точки получившейся системы ОДУ.
- Подобрав коэффициенты a, b, c, d и D1, D2, удовлетворяющие условиям, найденным в пункте 1, получить при численном счете так называемые структуры Тьюринга. Под структурой Тьюринга здесь понимается пространственно - неоднородное решение с волновым числом k, таким, что при записи решения в виде
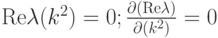 В случае линейной задачи эти структуры будут возрастать по амплитуде при
В случае линейной задачи эти структуры будут возрастать по амплитуде при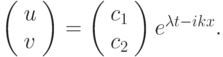
 ,
в случае нелинейного уравнения (следующая задача) бесконечный рост становится
невозможным, структура стабилизируется за счет нелинейности.
,
в случае нелинейного уравнения (следующая задача) бесконечный рост становится
невозможным, структура стабилизируется за счет нелинейности.
- Найти условие, когда внесение в систему диффузии приводит к потере устойчивости однородного стационарного решения.
-
Распределенный брюсселятор
Рассмотрим систему уравнений типа реакция - диффузия, где для описания химических реакций использована модельная система "брюсселятор". В литературе эта постановка имеет название "распределенный брюсселятор":
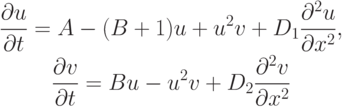
с граничными условиями

и начальным условием
 . Это — система уравнений "брюсселятор" с учетом диффузии компонентов.
. Это — система уравнений "брюсселятор" с учетом диффузии компонентов.- Пусть
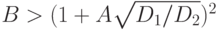 , D1 < D2. Рассмотреть образование структур Тьюринга в случаях
, D1 < D2. Рассмотреть образование структур Тьюринга в случаях 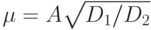 ,
, 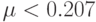 ,
, 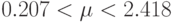 ,
, 
Когда можно пользоваться явной разностной схемой? Когда необходима неявная схема?
- Пусть теперь D1 > D2, A > 1. Что происходит в системе? Почему для расчетов необходимо применять неявные схемы? Какую схему расщепления по физическим процессам можно предложить для решения задачи? Примеры расчетов приведены в книге [12.15], качественное исследование — в [12.14, С. 403 - 407].
- Пусть
-
Схема "Классики"
Для двумерного уравнения теплопроводности используется схема "классики". Как и в схеме Саульева, расчет осуществляется в два этапа:
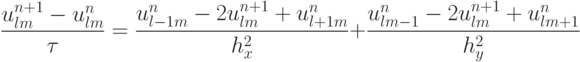
в случае, если l + m + n — четное,
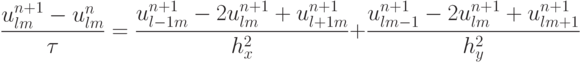
в случае, если l + m + n - нечетное.
Явная или неявная эта схема? Исследовать ее на аппроксимацию и устойчивость. Зачем нужно "перепрыгивание" — смена порядка обхода узлов при переходе со слоя на слой по времени?
Применить эту схему к расчету предыдущей задачи.
