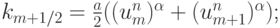НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1282 / 293 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

2.6. Задачи для самостоятельного решения

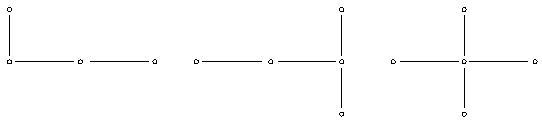
Используя условие устойчивости Куранта - Фридрихса - Леви, определить, какие из разностных схем, шаблоны которых приведены ниже, не будут устойчивыми:

Рис. 2.13.
При каком соотношении шагов $\tau$ и h явная разностная схема
$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = \frac{{u_{m - 1}^{n} - 2u_m^{n} + u_{{m} + 1}^{n}}}{h^2}$

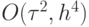для уравнения теплопроводности имеет порядок аппроксимации $O(\tau ^{2}, h^{4})$ ?
Показать, что параметрическая разностная схема
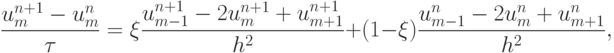
$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = \xi \frac{{u_{m - 1}^{n + 1} - 2u_m^{n + 1} + u_{{m} + 1}^{n + 1}}}{{h^2}} + (1 - \xi ) \frac{{u_{m - 1}^{n} - 2u_m^{n} + u_{{m} + 1}^{n}}}{{h^2}},$

при весе
$\xi = \frac{1}{2} - \frac{h^2}{12{\tau}}$
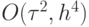имеет порядок аппроксимации $O(\tau ^{2}, h^{4})$ .
Для аппроксимации уравнения (2.2) использована схема
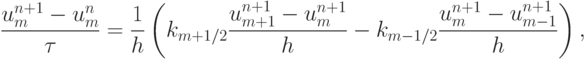
$\frac{{u_{m}^{{n} + {1}} - u_{m}^{n}}}{\tau} = \frac{1}{h} \left({k_{{m} + {1/2}} \frac{{u_{{m} + {1}}^{{n} + {1}} - u_{m}^{{n} + {1}}}}{h} - k_{{m} - {1/2}} \frac{{u_{m}^{{n} + {1}} - u_{{m} - {1}}^{{n} + {1}}}}{h}}\right),$

где k_{m + 1/2} вычисляется следующим образом:
- $$ k_{{m} + {1/2}} = \frac{a}{2}((u_{m}^{n} )^{\alpha} + (u_{m + 1}^{n} )^{\alpha} ) $;$
- $$ k_{{m} + {1/2}} = a \left({\frac{{u_{m}^{n} + u_{{m} + {1}}^{n}}}{2}}\right)^{\alpha} $;$
- $$ k_{{m} + {1/2}} = a \left({\frac{{2u_{m}^{n} u_{{m} + {1}}^{n}}}{{u_{m}^{n} + u_{{m} + {1}}^{n}}}}\right)^{\alpha}$;$
- $k_{{m} + {1/2}} = a \frac{{2(u_{m}^{n} )^{\alpha} (u_{{m} + {1}}^{n} )^{\alpha} }}{{(u_{m}^{n} )^{\alpha} + (u_{{m} + {1}}^{n} )^{\alpha} }}.$
Выражения a) - d) суть некоторые аппроксимации 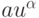$au^{\alpha}$ , взятые на предыдущем слое по времени между узлами u_m, u_{m +
1}. Какой из вариантов предпочтительнее? Почему не работают в окрестности фронта средние гармонические — c) и d)?

Реализовать схемы a) и b) на ЭВМ, сравнить численное решение с точным (см. выше). Почему при больших числах Куранта наблюдается отставание фронта волны в численном решении от точного значения [12.9]?
Режимы с обострением
Рассмотрим уравнение

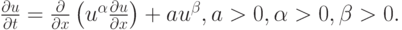
${\frac{{{\partial} u}}{{{\partial} t}} = \frac{{\partial}}{{{\partial} x}} \left({u^{\alpha} \frac{{{\partial} u}}{{{\partial} x}}}\right) + au^{\beta}, a > 0,{\alpha} > 0,{\beta} > 0.}$ ( 2.10)

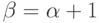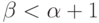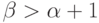Построить численно решение (2.10) в случаях а) ${\beta}={\alpha} + 1$ , б) ${\beta} <{\alpha} + 1$ , в) ${\beta} >{\alpha} + 1$ ,

$u \left({- \infty , t}\right) = 0 , u \left({+ \infty , t}\right) = 0 , u \left({x, 0}\right) = \left\{ \begin{array}{ll} u_0, & \left|{x}\right| \le 1, \\ {0}, & \left|{x}\right| > 1. \\ \end{array} \right.$

В чем качественное различие случаев а) (так называемый S - режим с обострением), б) ({HS} - режим), в) ({LS} - режим)? ([12.5, cм. глава 2], [12.4, С. 172 - 206]). В случае а) численно проверить справедливость формулы полуширины локализации тепла:
$l = {\pi}\sqrt{\frac{{\alpha + 1}}{{a{\alpha} ^2}}}$
. Как решение зависит от амплитуды начального возмущения u₀?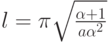
Автомодельные решения и автомодельные переменные
В случаях 1 - 3 будем искать решение уравнения (2.10) в виде [12.5, С. 32 - 62], [12.4]:

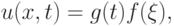
$u(x, t) = g(t)f(\xi ),$

где $\xi = x/ {\varphi}(t)$ .
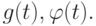
- Найти функции $g(t), {\varphi}(t).$
  (Ответ:
  $g(t) = (1 - t/t_f)^{- 1/2}, {\varphi}(t) = (1 - t/t_{f})^{\frac{{\beta - \left({\alpha + 1}\right)}}{{2 \left({\beta - 1}\right)}}}, t_f$
  — положительный параметр).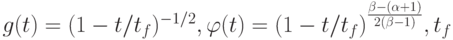
- Какому дифференциальному уравнению удовлетворяет при этом функция 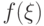$f(\xi )$ ? Решить численно получившееся уравнение для 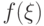$f(\xi )$ с условиями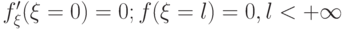
  $f^{\prime}_\xi (\xi = 0) = 0; f(\xi = l) = 0, l < + \infty$
  
  с дополнительным требованием $f^{\alpha} f^{\prime}_\xi |_{\xi = l} = 0$ .
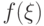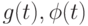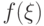- Задавая $f(\xi )$ при t = 0 в качестве начальных условий для (2.10), сравните поведение численного решения с автомодельным. (Так как известны $g(t), \phi (t)$ и $f(\xi )$ , то тем самым найдено 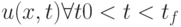$u(x, t) {\forall}t 0 < t < t_{f}$ ). Что происходит при $t \to t_{f}$ ?