Расчет освещенности. Файлы эффектов
Выходные данные вершинного шейдера мы описываем уже тройкой атрибутов: преобразованная вершина, преобразованная нормаль и вектор на источник света.
struct VS_OUTPUT
{
float4 position : POSITION;
float3 light : TEXCOORD0;
float3 normal : TEXCOORD1;
};Следует заметить, что атрибуты вершины нормаль и вектор на источник определены как текстурные координаты размерности 3 (float3). Тело вершинного шейдера будет выглядеть следующим образом.
VS_OUTPUT main_vs( VS_INPUT In )
{
VS_OUTPUT Out;
Out.position = mul( In.position, WorldViewProj );
float3 pos = mul( In.position, World );
Out.light = normalize(vecLight-pos);
Out.normal = normalize(mul( In.normal, World ));
return Out;
}Глобальные переменные будут такими же как и в предыдущем случае.
float4x4 WorldViewProj; float4x4 World; float4 vecLight;
Таким образом, пиксельный шейдер будет принимать на вход всего два вершинных атрибута: нормаль и вектор на источник. Сама же процедура пиксельного шейдера будет выглядеть так.
float4 main_ps(float3 light : TEXCOORD0, float3 normal : TEXCOORD1) : COLOR0
{
float4 diffuse = {1.0f, 1.0f, 0.0f, 1.0f};
return diffuse*dot(light, normal);
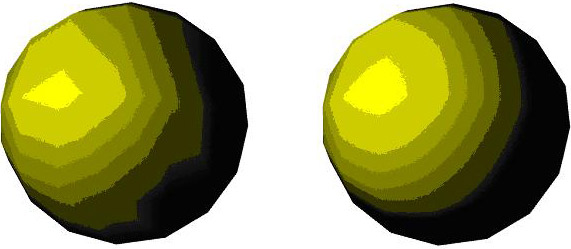
}Ниже приведены примеры закраски по методу Гуро (слева) и Фонга (справа).
Рассмотрим еще один очень распространенный эффект построения реалистичных изображений, называемый bump-mapping или микрорельефное текстурирование, причем без существенных вычислительных затрат. Идея этого подхода заключается в моделировании рельефной поверхности с помощью двух текстур. Одна из них представляет собой изображение некоторой поверхности, а другая – так называемая карта нормалей. Карта нормалей представляет собой текстуру, где каждый пиксель является вектором нормали. Можно сказать, что карта нормалей несет в себе информацию о неровностях в каждом пикселе изображения. Как известно интенсивность освещения зависит от угла между нормалью в точке и вектором на источник света (закон косинусов Ламберта).
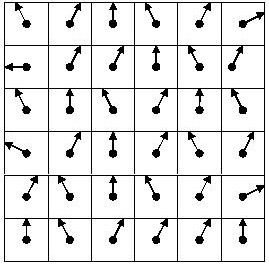
В зависимости от вектора нормали интенсивность в каждом пикселе будет различной. Следует заметить, что вектор нормали (nx, ny, nz) и цвет (R, G, B) кодируется тройкой чисел. Но цвет кодируется тремя положительными величинами из отрезка [0, 1], тогда как компоненты вектора нормали могут принимать и отрицательные значения. Так как координаты нормализованного вектора лежат в диапазоне [-1, 1], то можно с помощью линейного преобразования отобразить отрезок [-1, 1] в отрезок [0, 1]. Для этого можно воспользоваться следующей формулой: N*0.5+0.5, где N –вектор нормали. Такой процесс кодировки проделывается для каждого компонента вектора. Обратное преобразование (отрезок [0, 1] отобразить в отрезок [-1, 1] ) может быть реализовано с помощью формулы 2*C–1, где C – значение цвета. Например, вектор (1, 0, 1) будет преобразован в тройку чисел (1, 0.5, 1) – светло-фиолетовый цвет. Для получения карты нормалей из исходного изображения имеются специальные программы и алгоритмы, например, существует плагин к PhotoShop’у, с помощью которого можно получить карту нормалей. Ниже представлен пример текстуры и соответствующая ей карта нормалей.
Таким образом, для вычисления интенсивности в каждом пикселе необходимо:
- Получить цвет из исходной текстуры;
- Получить закодированное значение вектора нормали из карты нормалей;
- Произвести преобразование значений из цветового пространства в пространство нормалей;
- Вычислить скалярное произведение нормали на вектор источника света;
- Умножить полученное значение на цвет исходной текстуры.
Пиксельный шейдер, реализующий данные шаги показан ниже.
float4 Light;
sampler tex0;
sampler tex1;
struct PS_INPUT
{
float2 uv0 : TEXCOORD0;
float2 uv1 : TEXCOORD1;
float4 color: COLOR0;
};
float4 Main (PS_INPUT input): COLOR0
{
float4 texel0 = tex2D(tex0, input.uv0);
float4 texel1 = 2.0f*tex2D(tex1, input.uv1) - 1.0f;
return texel0*dot(normalize(Light), texel1);
};Значение положения источника света передается в пиксельный шейдер через переменную Light. Ниже показаны примеры микротекстурирования при различных положениях источника света.