Освещенность и материалы. Построения объектов

Освещенность и материалы

Для построения реалистичного изображения недостаточно только удалить невидимые грани объекта. После того как скрытые поверхности удалены, все видимые грани объекта необходимо закрасить, учитывая источники света, характеристики поверхностей, а также взаимное расположение и ориентацию поверхностей и источников света. В компьютерной графике выделяют, как правило, три типа источников света: точечный, параллельный и прожекторный. Более сложным с точки зрения моделирования, но зато более реалистичным источником света является точечный, при использовании которого освещенность поверхности зависит от ее ориентации: если лучи направлены перпендикулярно к поверхности, то она освещена максимально ярко, если же под углом, то освещенность ее убывает. Чем меньше угол падения лучей, тем меньше освещенность. Световая энергия, падающая на поверхность объекта, может быть поглощена, отражена или пропущена. Мы видим объект только благодаря тому, что он отражает или пропускает свет; если же объект поглощает весь падающий свет, то он невидим и называется абсолютно черным телом.

При расчете освещенности грани в компьютерной графике учитывают следующие типы отражения света от поверхности: рассеянное, диффузное, зеркальное. Интенсивность освещения граней объектов рассеянным светом считается постоянной в любой точке пространства. Это обусловлено тем, что рассеянный свет создается многочисленными отражениями от различных поверхностей пространства. Такой свет практически всегда присутствует в реальной обстановке. Даже если объект защищен от прямых лучей, исходящих от точечного источника света, он все равно будет виден из-за наличия рассеянного света. 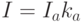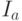Интенсивность рассеянного света выражается как , где - интенсивность рассеянного света, - коэффициент рассеянного отражения, зависящий от отражательных свойств материала (поверхности). При освещении объекта только рассеянным светом, все его грани будут закрашены одинаково, а общие ребра будут неразличимы.

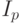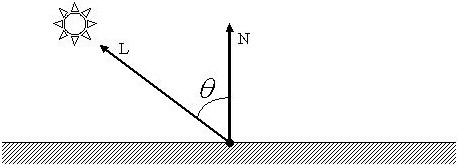
При наличии в сцене точечного источника света, интенсивность диффузного отражения пропорциональна косинусу угла между нормалью к поверхности и направлением на источник света. В этом случае для вычисления интенсивности диффузного отражения применяют закон косинусов Ламберта: , где - интенсивность точечного источника света, - коэффициент диффузного отражения, - угол падения, рассчитываемый как угол между направлением на источник света и нормалью к поверхности. Если вектора N, L нормализованы, т.е. |N|=|L|=1, то - скалярное произведение векторов, и уравнение можно записать в виде .

Свойством диффузного отражения является равномерность по всем направлениям отраженного света. Поэтому такие объекты имеют одинаковую яркость, вне зависимости от угла обзора. К примеру, матовые поверхности обладают таким свойством. Предположим, что у нас имеется два полигона, одинаково ориентированы относительно источника света, но расположенные на разных расстояниях от него. Если вычислить значения интенсивностей освещенности для каждого полигона, по приведенной формуле, то они окажутся одинаковыми. Это означает, что объекты, расположенные на разном расстоянии от источника света, будут освещаться независимо от их местоположения в трехмерной сцене. В этом случае интенсивность света должна быть обратнопропорциональна квадрату расстояния от источника до грани объекта. Тогда объект, расположенный дальше от источника будет темнее. Тем не менее на практике, как правило, используют не квадрат расстояния, а линейное затухание. В этом случае формула общей интенсивности может быть записана как:

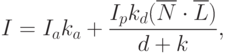
Зеркальное отражение можно получить от любой блестящей поверхности. Осветите ярким светом обычное яблоко, и световой блик возникнет в результате зеркального отражения, а свет, отраженный от остальной части яблока, появится вследствие диффузного отражения. Следует отметить, что в том месте, где находится световой блик, яблоко будет казаться не красным, а, скорее всего – белым, т.е. окрашенным в цвет падающего света. Если изменить положение наблюдателя, то световой блик тоже сместится. Это объясняется тем, что блестящие поверхности отражают свет неодинаково по всем направлениям. От идеально зеркальной поверхности свет отражается только в том направлении, для которого углы падения и отражения совпадают. Зеркально отраженный свет можно будет увидеть, если угол между вектором отражения (на рисунке обозначен R ) и вектором наблюдения (на рисунке обозначен S ) равен нулю.

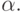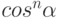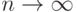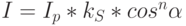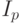Для неидеальных отражающих поверхностей интенсивность отраженного света резко падает с ростом В модели, предложенной Фонгом, быстрое убывание интенсивности света, описывается функцией , где в зависимости от вида поверхности. Для идеальной отражающей поверхности . Интенсивность зеркального отражения света по модели Фонга записывается как , где - интенсивность источника света, - коэффициент зеркального отражения. Если вектора R и S нормированы, то формула может быть преобразована к виду:

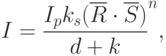
Таким образом, интенсивность грани складывается из трех составляющих: рассеянного света, диффузного света и зеркального света. Формула расчета общей интенсивности с учетом расстояния от наблюдателя до освещенной грани и трех составляющих света записывается как

Для более реалистичного отображения объектов сцены в библиотеке Direct3D определены понятия материал и свет. Материал в Direct3D задает свойства поверхности отображаемых примитивов. С помощью материала определяется как будет отражаться от поверхности примитива свет. Материал и свет (в контексте Direct3D ) используются совместно. Одно без другого работать не будет.

Для работы с материалом предусмотрен специальный тип данных D3DMATERIAL9, который содержит следующие поля.

typedef struct _D3DMATERIAL9 {
  D3DCOLORVALUE Diffuse;   {рассеянный свет, исходящий от материала}
  D3DCOLORVALUE Ambient;   {определяет окружающий свет}
  D3DCOLORVALUE Specular;  {определяет отражающий (зеркальный) свет}
  D3DCOLORVALUE Emissive;  {определяет излучающий свет материала}
  float Power;             {мощность отражения}
} D3DMATERIAL9;

TD3DMaterial9 = packed record
 Diffuse: TD3DColorValue;  {рассеянный свет, исходящий от материала}
 Ambient: TD3DColorValue;  {определяет окружающий свет}
 Specular: TD3DColorValue; {определяет отражающий (зеркальный) свет}
 Emissive: TD3DColorValue; {определяет излучающий свет материала}
 Power: Single;            {мощность отражения}
end;