Лекция 6: Некоторые задачи нелинейного программирования и нахождение опорного плана для задачи линейного программирования
Особенности применения косинуса как функции меры угла
О величине угла в n -мерном пространстве мы можем судить только
по его косинусу. Однако косинус не является монотонной функцией и в
общем случае может служить мерой угла, если диапазон изменения этого
угла не превышает 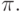
Составим по (6.11) симметричную матрицу S, включенную в табл. 6.1 косинусов углов между всеми нормалями к граням верхней (нижней) поверхности выпуклого многогранника R.
| Грань | Нормаль | N1 | N2 | ... | Nr+n |
|---|---|---|---|---|---|
| p1 | N1 | 1 | cos(N1,N2) | ... | cos(N1,Nr+n) |
| p2 | N2 | cos (N2,N1) | 1 | ... | cos(N2,Nr+n) |
| ... | ... | ... | ... | ... | ... |
| pr | Nr | cos(Nr,N1) | cos(Nr,N2) | ... | cos(Nr,Nr+n) |
| pr+1 | Nr+1 | cos(Nr+1,N1) | cos(Nr+1,N2) | ... | cos(Nr+1,Nr+n) |
| ... | ... | ... | ... | ... | ... |
| pr+n | Nr+n | cos(Nr+n, N1) | cos(Nr+n,N2) | ... | 1 |
Выберем строку, соответствующую некоторой грани. Для
комплектации граней, совместно с выбранной образующих общую вершину,
выделим в этой строке n минимальных отличных от 0 и  углов, то есть n максимальных косинусов, отличных от 1 и -1. Тем самым мы отдаем
предпочтение вершинам с наиболее "пологими" склонами. При корректно
сформулированной задаче такие грани "вокруг" некоторых вершин должны
найтись. При этом углы между нормалями к граням, образующим общую
вершину, не превышают
углов, то есть n максимальных косинусов, отличных от 1 и -1. Тем самым мы отдаем
предпочтение вершинам с наиболее "пологими" склонами. При корректно
сформулированной задаче такие грани "вокруг" некоторых вершин должны
найтись. При этом углы между нормалями к граням, образующим общую
вершину, не превышают 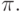 Следовательно, косинус может служить
функцией меры углов в диапазоне их изменения.
Следовательно, косинус может служить
функцией меры углов в диапазоне их изменения.
Поясним выбор последовательности n косинусов.
Выбранная грань может быть параллельна некоторой другой грани или
координатной плоскости, т.е. угол между их нормалями может быть равен
либо нулю, либо 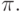 Очевидно, такие грани не могут быть
образующими
одной вершины.
Очевидно, такие грани не могут быть
образующими
одной вершины.
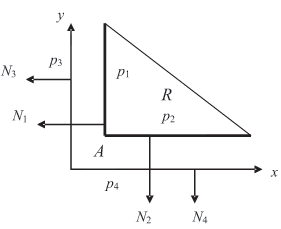
На рис. 6.6 Qнижн={p1, p2, p3, p4}.
Таблица косинусов углов имеет вид
Из первой строки, допуская лишь одну единицу cos(N1,N1)=1 ), находим возможные образующие {p1, p2}. При этом поиск элементов последовательности ведем слева направо. Проверка подтверждает правильность выбора вершины A. Аналогично, из второй строки находим {p2, p1}, что определяет ту же вершину. Третья строка определяет возможное множество образующих {p3, p2}, что не подтверждается проверкой. Четвертая строка также не определяет правильный выбор образующих {p4, p1}.
Обратим внимание на то, что все вышесказанные предположения и теоремы касаются граней, о которых доподлинно известно, что они входят в состав поверхности многогранника допустимых решений. Важным источником неприятностей являются координатные плоскости. Ведь мы не знаем, являются ли они действительными гранями, и вынуждены относить их к возможным. Отсюда и возможная ошибочность выводов.
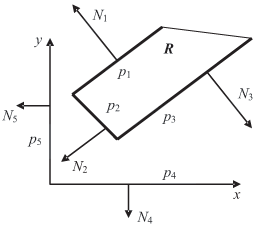
На рис. 6.7 Qнижн={p1, p2, p3, p4, p5}.
Таблица косинусов углов имеет вид
| Грань | Нормаль | N1 | N2 | N3 | N4 | N5 |
|---|---|---|---|---|---|---|
| p1 | N1 | 1 | 0 | -1 | - 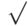 2/2 2/2 |
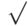 2/2 2/2 |
| p2 | N2 | 0 | 1 | 0 |
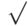 2/2 2/2 |
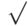 2/2 2/2 |
| p3 | N3 | -1 | 0 | 1 |
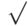 2/2 2/2 |
- 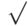 2/2 2/2 |
| p4 | N4 | - 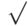 2/2 2/2 |
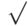 2/2 2/2 |
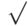 2/2 2/2 |
1 | 0 |
| p5 | N5 |
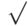 2/2 2/2 |
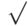 2/2 2/2 |
- 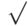 2/2 2/2 |
0 | 1 |
Легко видеть, что анализ любой строки не позволит обнаружить вершину многогранника R.
Действительно, по первой строке формируется предполагаемое множество образующих {p1, p4}. Однако пересечение этих прямых не дает искомую вершину. И так — по всем строкам. Если бы было установлено, что ось y не входит в состав поверхности R, то соответствующий косинус можно бы было игнорировать, что привело бы к правильному выбору множества образующих {p1, p2}.
Анализ этого примера наводит на мысль: обязательно ли формировать верхнюю (нижнюю) поверхность до конца, присоединяя координатные плоскости? Ведь количество действительных граней, составляющих ее, достаточно для осуществления поиска вершины. А именно, если в выражении (6.7) r >= n, то на первом этапе поиска исключим из рассмотрения координатные плоскости. Это приведет к исключению из табл. 6.3 двух последних строк и столбцов. Легко видеть, что поиск вершины осуществляется успешно.
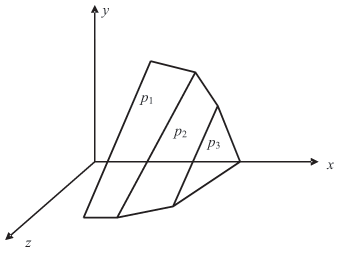
На рис. 6.8 демонстрируется случай, когда, несмотря на выполнение указанного выше неравенства, к поиску вершины необходимо подключать координатные плоскости.
Три плоскости p1, p2, p3 совместно не являются образующими одной вершины. Только включение в рассмотрение плоскостей z = 0 или y = 0 позволяет найти вершины многогранника допустимых решений.
Грань может иметь нормаль, угол которой с нормалями некоторых
"далеких" граней превышает 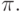 Например, углы между
нормалями к
координатным плоскостям составляют
Например, углы между
нормалями к
координатным плоскостям составляют  . Здесь
использование косинуса может привести к неоднозначности при
упорядочении углов.
. Здесь
использование косинуса может привести к неоднозначности при
упорядочении углов.
Тогда воспользуемся следующим предположением:
На верхней (нижней) поверхности выпуклого многогранника R
существует грань, нормаль к которой составляет с нормалями ко всем другим
граням этой поверхности углы, не превышающие 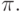
Это — предположение об обязательном существовании некоторых
"срединных" граней, нормали к которым близки к середине диапазона
изменения таких нормалей, — диапазона ![[0, \frac{{3\pi }}{2}]](/sites/default/files/tex_cache/42a423b392f6e7753981088603683005.png) .
.
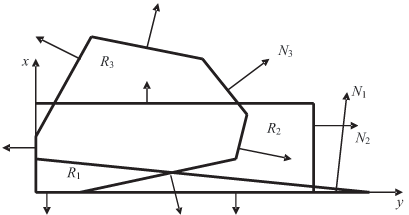
На рис. 6.9 отражена попытка представления некоторых крайних случаев, иллюстрирующих на плоскости существование "срединных" граней для разных выпуклых многогранников.
Так, в многограннике R1 (треугольник) угол между нормалью N1
и другими нормалями не превышает 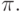 В прямоугольнике R2
максимальный угол, например, между нормалью N2 и другими
нормалями,
составляет
В прямоугольнике R2
максимальный угол, например, между нормалью N2 и другими
нормалями,
составляет 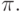 В многоугольнике R3, к примеру,
нормаль N3
составляет со всеми нормалями угол, меньше
В многоугольнике R3, к примеру,
нормаль N3
составляет со всеми нормалями угол, меньше 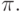
Таким образом, мы предположили существование хотя бы одной грани, при анализе которой с помощью косинусов удается избежать искажений в определении того, в каком отношении находятся углы, которые нормаль к этой грани образует с нормалями к другим граням поверхности. Исключается случай, когда большему углу соответствует и больший косинус. Это приводит к необходимости одновременного параллельного анализа многих граней поверхности в качестве начальных, так как успех может быть достигнут не всегда.