Лекция 4: Параллельные и сетевые технологии решения задач линейного программирования
Параллельное решение задачи целочисленного линейного программирования
Методы параллельного решения задачи ЛП, основанные на непосредственном перемещении по ребрам многогранника решений, не привлекая дополнительных переменных, способствуют построению наглядного метода решения соответствующей задачи линейного программирования (задачи ЦЛП). Под соответствием мы понимаем добавление условия целочисленности решения при той же формальной постановке задачи ЛП.
Такой метод основан на захвате в "вилку" некоторой целой точки внутри многогранника решений, вблизи точки решения задачи ЛП.
Рассмотрим пример.
Решим задачу ЦЛП:
Z = x - 3y + 3z -> max
при ограничениях
2x + y - z <= 4
4x - 3y <= 2
-3x + 2y + z <= 6
и при условиях x, y, z >= 0, целые.
Решение задачи ЛП достигается (рис. 4.5) в точке (0,5, 0, 7,5), которая является результатом решения системы уравнений — граней
q2 = 4x - 3y - 2 = 0
q3 = -3x + 2y + z - 6 = 0
q5 = y = 0
Значение целевой функции Z(0,5, 0, 7,5) = 23.
Положим 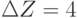 , и найдем все точки пересечения
образовавшейся "целевой плоскости" с ребрами, исходящими из
вершины-решения. Для ребра (q2, q3)
, и найдем все точки пересечения
образовавшейся "целевой плоскости" с ребрами, исходящими из
вершины-решения. Для ребра (q2, q3)
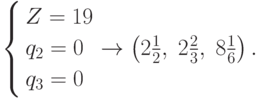
Для ребра (q2, q5)
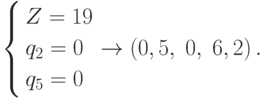
Для ребра (q3, q5)
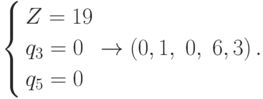
Значит, только в точке  наблюдается "преодоление" целых значений по сравнению с точкой (0,5,
0, 7,5), представляющей точное решение задачи ЛП. Т.е. нам удалось
захватить решение задачи ЦЛП в "вилку". При этом точка (2,
2, 8),
"преодоление" которой произошло, — возможное решение задачи
ЦЛП.
наблюдается "преодоление" целых значений по сравнению с точкой (0,5,
0, 7,5), представляющей точное решение задачи ЛП. Т.е. нам удалось
захватить решение задачи ЦЛП в "вилку". При этом точка (2,
2, 8),
"преодоление" которой произошло, — возможное решение задачи
ЦЛП.
Однако для того, чтобы координате z преодолеть ближайшее целое
значение, координатам x и y пришлось преодолеть по
два целых
значения. Поэтому закономерен вопрос о том, нет ли внутри отсеченной с
помощью 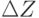 области целых точек, где z
преодолевает ближайшее
целое с меньшей ценой для других координат. Ведь значение целевой
функции в таких точках было бы больше.
области целых точек, где z
преодолевает ближайшее
целое с меньшей ценой для других координат. Ведь значение целевой
функции в таких точках было бы больше.
Половиним "вилку". Положим 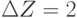 и найдем
точки пересечения
"целевой плоскости" Z = 21 c ребрами, исходящими из
вершины-решения
задачи ЛП:
и найдем
точки пересечения
"целевой плоскости" Z = 21 c ребрами, исходящими из
вершины-решения
задачи ЛП:
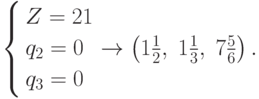
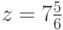 , которая не
"преодолела" ближайшее целое, определяемое решением задачи ЛП. Там z =7,5. Очевидно, что на других двух ребрах ситуация тем более
останется
прежней.
, которая не
"преодолела" ближайшее целое, определяемое решением задачи ЛП. Там z =7,5. Очевидно, что на других двух ребрах ситуация тем более
останется
прежней.Вновь половиним "вилку" в сторону увеличения значения 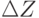 , пытаясь вплотную подойти к возможной целой точке, где значение Z
максимально. Положим
, пытаясь вплотную подойти к возможной целой точке, где значение Z
максимально. Положим 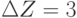 . Найдем точки пересечения
"целевой
плоскости" Z = 20 с ребрами, исходящими из вершины-решения
задачи
ЛП.
. Найдем точки пересечения
"целевой
плоскости" Z = 20 с ребрами, исходящими из вершины-решения
задачи
ЛП.
Решаем первую систему.
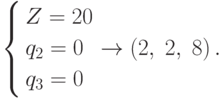
Если бы решение не совпало с целым, мы проверили бы точки пересечения "целевой плоскости" с другими ребрами. Вместе с тем, это можно и не делать, т.к. для меньшего значения Z = 19 уже установлен факт "непреодоления" там целых значений. Так что нам осталось бы только выполнить округление.
Рассмотренные в лекции методы решения задач линейного программирования имеют важную методологическую направленность, обусловленную наглядностью, ощутимостью, чувством "физического смысла" задач. Их роль не осмысленна до конца, но они позволяют эффективно распараллеливать вычисления. В этом смысле такие методы, как симплекс-метод, венгерский метод ориентированы исключительно на последовательные вычисления, но зато полностью исключают перебор. Для большой размерности задачи введение дополнительных переменных, что предполагается в симплекс-методе, может показаться нежелательным.
Предложен вполне практический метод (хотя и не описан алгоритмически) решения задачи ЦЛП, опирающийся на нахождение хотя бы одного решения соответствующей задачи ЛП. Мы не затронули вопроса о единственности решения — как задачи ЛП, так и задачи ЦЛП, о произвольном числе ребер, образующих вершину-решение задачи ЛП. Метод, несомненно, подлежит развитию. Его достоинство заключается в том, что он, по сравнению с методом "ветвей и границ", не требует многократного решения задачи ЛП с динамически уточняющимися и размножающимися ограничениями.
Можно указать на осуществляемое практическое применение предлагаемых методов в качестве тестовых задач для оценки эффективности многопроцессорных ВС, использующих принципы SPMD-технологии ("единственная программа — много потоков данных"). Эти же методы используются при разработке сетевых технологий решения сложных задач.